JAC Class 9 Science Important Questions Chapter 8 गति

Jharkhand Board JAC Class 9 Science Important Questions Chapter 8 गति Important Questions and Answers.

JAC Board Class 9 Science Important Questions Chapter 8 गति

वस्तुनिष्ठ प्रश्न

1. गाड़ी द्वारा चली गयी दूरी बतायी जाती है-
(a) स्पीडोमीटर से
(b) ओडोमीटर से
(c) मेनोमीटर से
(d) सीस्मोग्राफ़ से।
उत्तर:
(b) ओडोमीटर से।

2. त्वरण का S.I. मात्रक है-
(a) मी/से.²
(b) मी/से.
(c) किग्रा.मी/से.
(d) न्यूटन/मीटर।
उत्तर:
(a) मी/से.²

3. किसी वस्तु की गति के लिए दूरी-समय ग्राफ, समय अक्ष के समान्तर एक सरल रेखा है। यह ग्राफ प्रदर्शित करता है-
(a) एक समान गति
(b) समान वेग
(c) त्वरित गति
(d) विरामावस्था।
उत्तर:
(d) विरामावस्था।

4. 36 किमी/घण्टा की चाल से चल रही कार 10 मिनट में कितनी दूरी तय करेगी-
(a) 6 किमी
(b) 36 किमी
(c) 3.6 किमी
(d) 0.36 किमी।
उत्तर:
(a) 6 किमी।

5. वेग परिवर्तन की दर को कहते हैं-
(a) विस्थापन
(b) चाल
(c) त्वरण
(d) संवेग।
उत्तर:
(c) त्वरण।

6. दिए गए सूत्र में रिक्त स्थान भरिए-
S = ut + ……………………..
(a) at
(b) 2as
(c) at²
(d) \(\frac { 1 }{ 2 }\)at²
उत्तर:
(d) \(\frac { 1 }{ 2 }\)at²

7. किसी वस्तु की गति के लिए चाल समय ग्राफ, समय अक्ष के समान्तर एक सरल रेखा है। यह ग्राफ प्रदर्शित करता है।
(a) एक समान त्वरित गति
(b) एक समान चाल
(c) असमान त्वरित गति
(d) विरामावस्था।
उत्तर:
(b) एक समान चाल।

8. कोई कार 54 किमी/घण्टा की चाल से चल रही है। 5 सेकण्ड पश्चात् उसकी चाल 72 किमी/ घण्टा हो जाती है उसका त्वरण होगा-
(a) 2मी/से
(c) मी/से²
(b) 4मी/से²
(d) \(\frac { 1 }{ 2 }\) मी/से²।
उत्तर:
(c) 1 मी/से²।

9. विरामावस्था से गतिशील होकर किसी पिण्ड का त्वरण 8 ms^-2 हो जाता है। पिण्ड द्वारा 1 सेकण्ड में चली गई दूरी होगी-
(a) 6m
(b) 4m
(c) 2m
(d) &m
उत्तर:
(b) 4m।

10. एक कार 54 किमी / घण्टा की चाल से गतिमान है, मी/से में इसकी चाल है-
(a) 20 मी/से.
(b) 194.4 मी/से.
(c) 15 मी/से.
(d) 18 मी/से.।
उत्तर:
(c) 15 मी / से।

11. A से B तक तय की गयी दूरी है-

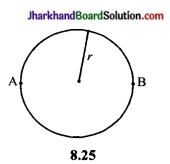
(a) 2r
(b) 2πr
(c) πr
(d) \(\frac { πr }{ 2 }\)
उत्तर:
(c) πr

12. प्रश्न 11 वाले चित्र में बिन्दु A से B तक का विस्थापन है-
(a) 2r
(b) 2 πr
(c) πr
(d) शून्य।
उत्तर:
(a) 2r।

13. 20 किमी / घण्टा की चाल से गतिशील किसी कार की चाल 6 सेकण्ड में 60 किमी / घण्टा हो जाती है।
कार का त्वरण है-
(a) 240 किमी / घण्टा²
(b) 24 किमी / घण्टा²
(c) 2400 किमी / घण्टा²
(d) \(\frac { 1 }{ 240 }\) किमी/ घण्टा²।
उत्तर:
(c) 2400 किमी / घण्टा²।

14. विस्थापन का SI मात्रक है-
(a) m/s
(b) m/s²
(c) km/h
(d) m.
उत्तर:
(d) m.

15. निम्नांकित ग्राफ दर्शाता है-

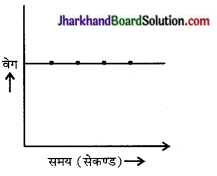
(a) वस्तु स्थिर है
(b) वस्तु स्थिर वेग से गतिमान है।
(c) वस्तु का वेग एक समान दर से परिवर्तित हो रहा है
(d) वस्तु का त्वरण असमान है।
उत्तर:
(b) वस्तु स्थिर वेग से गतिमान है।

रिक्त स्थान भरो-

1. दूरी एक ……………………. राशि है।
2. विस्थापन एक ……………………. राशि है।
3. विस्थापन का अंकीय मान ……………………. होता है जब प्रारम्भिक और अंतिम स्थिति एक हो ।
4. यदि वस्तु की गति समय के साथ लगातार घटती है तो वह ……………………. गति कहलाती है।

उत्तर:

1. अदिश
2. सदिश
3. शून्य
4. मंदन।

सुमेलन कीजिए-

कॉलम ‘क’	कॉलम ‘ख’
1. प्रथम समीकरण	(क) v² – u² = 2as
2. द्वितीय समीकरण	(ख) v = u + at
3. तृतीय समीकरण	(ग) s – u t = \(\frac { 1 }{ 2 }\) at²

उत्तर:
1. (ख) v = u + at
2. (ग) s – u t = \(\frac { 1 }{ 2 }\) at²
3. (क) v² – u² = 2as

सत्य / असत्य-

1. मंदन की स्थिति में त्वरण ऋणात्मक होता है।
2. यदि वस्तु की गति समय के साथ लगातार घटती है तब वह त्वरण गति कहलाती है।
3. विस्थापन शून्य नहीं हो सकता।
4. दूरी का मान शून्य नहीं हो सकता।

उत्तर:

1. सत्य
2. असत्य
3. असत्य
4. सत्य।

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
चाल को परिभाषित कीजिए।
उत्तर:
किसी वस्तु द्वारा किसी भी दिशा में इकाई समय में चली गयी दूरी को चाल कहते हैं।

प्रश्न 2.
एक वस्तु एक समान वेग से चल रही है। इसका त्वरण ज्ञात कीजिए।
उत्तर:
शून्य।

प्रश्न 3.
क्या किसी गतिमान वस्तु का औसत वेग शून्य हो सकता है ?
उत्तर:
हाँ, जब उसका किसी दिये गये समय में विस्थापन शून्य हो।

प्रश्न 4.
किसी वस्तु की चाल नियत है। क्या उसमें त्वरण हो सकता है ? उदाहरण दीजिये।
उत्तर:
चाल नियत होने पर भी वस्तु में त्वरण हो सकता है, यदि वह वृत्तीय गति में है जैसे कृत्रिम उपग्रहों की पृथ्वी के चारों ओर गति, इलेक्ट्रॉन की नाभिक के चारों ओर गति ।

प्रश्न 5.
एक वस्तु द्वारा तय की गई दूरी समय के अनुक्रमानुपाती है, उसकी चाल कैसी होगी?
उत्तर:
पिण्ड की चाल एक समान होगी।

प्रश्न 6.
एक गेंद वायु में ऊपर फेंकी गई गेंद का त्वरण तथा वेग सबसे ऊपर वाले भाग में क्या होगा?
उत्तर:
त्वरण 9.8m/s² है जो नीचे की ओर कार्य करता है तथा उसका वेग शून्य होगा।

प्रश्न 7.
वेग की परिभाषा लिखिए।
उत्तर:
विस्थापन परिवर्तन की दर वेग कहलाती है।

प्रश्न 8.
एक समान त्वरित गति का एक उदाहरण दीजिए।
उत्तर:
पृथ्वी पर स्वतन्त्रतापूर्वक गिरती हुई वस्तु की गति।

प्रश्न 9.
मन्दन किसे कहते हैं?
उत्तर:
ऋणात्मक त्वरण को मन्दन कहते हैं।

प्रश्न 10.
विरामावस्था अवस्था किसे कहते हैं?
उत्तर:
ऐसी अवस्था जब वस्तु की चाल शून्य हो, विरामावस्था कहलाती है।

प्रश्न 11.
चाल तथा वेग का SI मात्रक क्या है?
उत्तर:
मीटर / सेकण्ड।

प्रश्न 12.
एकसमान वृत्तीय गति से क्या तात्पर्य है?
उत्तर:
एकसमान वृत्तीय गति यदि कोई वस्तु समान समयान्तराल में वृत्तीय पथ पर समान दूरी तय करती है तो वस्तु की गति एकसमान वृत्तीय गति कहलाती है।

प्रश्न 13.
कोई वस्तु 10 मीटर/सेकण्ड के वेग से गति कर रही है, यदि उसकी गति एकर शन हो तो 10 सेकण्ड पश्चात् उसका वेग क्या होगा?
उत्तर:
चूँकि वस्तु की गति एकसमान है; अतः उसका वेग अपरिवर्तित रहेगा अर्थात् 10 सेकण्ड पश्चात् भी उसका वेग 10 मीटर / सेकण्ड ही रहेगा।

प्रश्न 14.
एक कार का दूरी-समय ग्राफ निम्नांकित चित्र में प्रदर्शित है। बताइए-

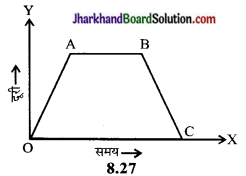
(i) ग्राफ का कौन-सा भाग कार की विरामावस्था को प्रदर्शित करता है?
(ii) AB भाग में कार के वेग की प्रकृति क्या है?
(iii) कौन-सा भाग कार के वापस लौटने को प्रदर्शित करता है?
उत्तर:
(i) A से B तक का भाग विरामावस्था को प्रदर्शित करता है।
(ii) OA भाग में कार का वेग एकसमान है।
(iii) BC भाग कार के वापस लौटने को प्रदर्शित करता है।

प्रश्न 15.
निम्नलिखित में से उस ग्राफ को पहचानिए जो – (a) एकसमान मंदन, (b) शून्य त्वरण की गति को प्रदर्शित करता है।

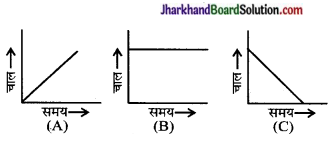
उत्तर:
(a) ग्राफ C में चाल एकसमान रूप से घटती है; अतः यह एकसमान मन्दन को प्रदर्शित करता है।
(b) ग्राफ B में वस्तु स्थिर चाल से गतिमा है; अत: यह ग्राफ शून्य त्वरण की गति को प्रदर्शित करता है।

प्रश्न 16.
एक गेंद मेज पर गति करती हुई उसके किनारे पहुँचती है और नीचे गिर पड़ती है। नीचे गिरते समय इसके द्वारा तय किए गए मार्ग को प्रदर्शित कीजिए। इस पथ का नाम भी बताइए।

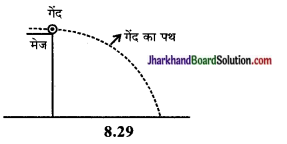
उत्तर:
गेंद का पथ परवलयाकार होगा।

प्रश्न 17.
वेग समय ग्राफ का ढलान क्या प्रदर्शित करता है?
उत्तर:
वेग समय ग्राफ का ढलान (slope) त्वरण को प्रदर्शित करता है।

प्रश्न 18.
अगर किसी वस्तु का वेग समय ग्राफ, समय अक्ष के समान्तर हो, तो इससे क्या निष्कर्ष निकलता है?
उत्तर:
पिण्ड का वेग एक समान है अर्थात् पिण्ड का त्वरण शून्य है।

प्रश्न 19.
कोई वस्तु समान समय में समान दूरी तय करती है। इसके दूरी-समय ग्राफ का ढलान क्या होगा?
उत्तर:
एक सीधी सरल रेखा होगी जो x अक्ष के साथ कोई कोण बनाती है।

प्रश्न 20.
कोई वस्तु समान समय अन्तरालों में समान दूरी तय करती है। इसके चाल-समय ग्राफ का ढलान क्या होगा?
उत्तर:
यह एक सीधी रेखा होगी जो समय अक्ष के समान्तर होती है।

प्रश्न 21.
यदि किसी वस्तु का विस्थापन समय ग्राफ एक सीधी रेखा हो जो समय के साथ एक कोण बनाती है। गति की प्रकृति कैसी होगी ?
उत्तर:
एकसमान गति।

प्रश्न 22.
यदि किसी वस्तु का विस्थापन समय ग्राफ समय अक्ष के समान्तर हो तो वस्तु की गति कैसी होगी?
उत्तर:
वस्तु विराम अवस्था में है।

प्रश्न 23.
वस्तु की गति के बारे में आप क्या बता सकते हैं, यदि
(a) उसका विस्थापन समय ग्राफ एक सीधी रेखा है।
(b) उसका वेग समय ग्राफ एक सीधी रेखा है।
उत्तर:
(a) एक समान वेग
(b) एक समान त्वरण।

प्रश्न 24.
S.I. पद्धति में त्वरण का मात्रक लिखिए।
उत्तर:
S. I. पद्धति में त्वरण का मात्रक मीटर/सेकण्डर² है।

प्रश्न 25.
निम्नलिखित गति के समीकरण में खाली स्थान भरिए – s = ……………… + \(\frac { 1 }{ 2 }\) at²
उत्तर:
गति का समीकरण s = ut + \(\frac { 1 }{ 2 }\) at²

प्रश्न 26.
गति के समीकरण v² + ……………… + 2as को पूर्ण कीजिए।
उत्तर:
गति का समीकरण v² = u² + 2 a s

प्रश्न 27.
समय-दूरी ग्राफ का ढाल क्या प्रदर्शित करता है?
उत्तर:
समय-दूरी ग्राफ का ढाल चाल को प्रदर्शित करता है।

प्रश्न 28.
यदि समय विस्थापन ग्राफ, समय- अक्ष के समान्तर एक सरल रेखा में हो तो वेग तथा त्वरण के मान होंगे?
उत्तर:
वेग तथा त्वरण दोनों के मान शून्य होंगे।

प्रश्न 29.
समय वेग ग्राफ का ढाल क्या प्रदर्शित करता है?
उत्तर:
समय वेग ग्राफ का ढाल त्वरण को प्रदर्शित करता है।

प्रश्न 30.
समय वेग ग्राफ में त्वरण किसके बराबर होता है?
उत्तर:
ग्राफ रेखा के ढाल के बराबर होता है।

प्रश्न 31.
क्या संलग्न चित्र 8.30 में प्रदर्शित किसी वस्तु का समय दूरी ग्राफ सही है? कारण सहित स्पष्ट कीजिए।

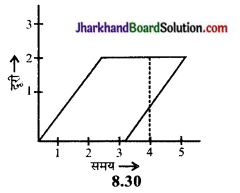
उत्तर:
ग्राफ सही नहीं है। इस ग्राफ में एक ही समय (जैसे-4 सेकण्ड) पर वस्तु को दो अलग-अलग स्थानों पर दिखाया गया है जो कि असम्भव है।

प्रश्न 32.
एक वस्तु त्रिज्या के वृत्त पर गति कर रही है। उसके द्वारा चली दूरी व विस्थापन कितना होगा?
(i) आधे चक्कर के बाद
(ii) पूरा चक्कर हो जाने पर।
उत्तर:
(i) आधा चक्कर पूरा हो जाने पर चली दूरी तथा विस्थापन 21 होगा।
(ii) चक्कर पूरा हो जाने पर चली दूरी 2xr तथा विस्थापन शून्य होगा।

प्रश्न 33.
गति का समीकरण लिखिए जबकि गतिशील वस्तु में त्वरण न होकर मन्दन हो रहा है।
उत्तर:
मन्दन होने पर त्वरण ऋणात्मक होगा। अतः गति के समीकरण निम्नवत् होंगे-

• v = u – at,
• s = ut – \(\frac { 1 }{ 2 }\) at²
• v² – u² – 2 as.

प्रश्न 34.
एक वस्तु एकसमान वेग से चल रही है, गति के समीकरणों का स्वरूप बताइए।
उत्तर:
जब वस्तु एकसमान वेग से चल रही है तो त्वरण a = 0:

• v = u.
• s = ut
• v² = u²

प्रश्न 35.
कोई वस्तु विरामावस्था से अचर त्वरण से चलना प्रारम्भ करती है, तो गति के समीकरणों का स्वरूप बताइए।
उत्तर:
जब वस्तु विरामावस्था से चल रही है, तो u = 0

• v = at
• s = \(\frac { 1 }{ 2 }\) at²
• v² = 2 as

प्रश्न 36.
गति के समीकरण v = u + at का अर्थ समझाइए।
उत्तर:
गति के समीकरण v = u + at का अर्थ है-
t समय पश्चात् वस्तु का अन्तिम वेग प्रारम्भिक वेग + त्वरण समय।

प्रश्न 37.
वृत्तीय गति किसे कहते हैं?
उत्तर:
वृत्तीय गति – जब कोई वस्तु वृत्ताकार पथ पर गति करती है तो उस वस्तु की गति वृत्तीय गति कहलाती है।

लघुत्तरात्मक एवं दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
एकसमान गति व असमान गति को दूरी समय आरेख से समझाइए।
उत्तर:
समान गति यदि कोई वस्तु निश्चित समय अन्तराल में समान दूरी तय करती है, तो वस्तु की गति को एकसमान गति कहते हैं।

उदाहरण – यदि हम एक कार से सड़क पर एकसमान चाल से गतिमान हैं, तो माना हम निम्नलिखित प्रेक्षण प्राप्त करते हैं-

किलोमीटर पत्थर की संख्या (दूरी)	समय (सेकण्ड में)
मूल पत्थर	0
1 किमी पत्थर	100 सेकण्ड
2 किमी पत्थर	200 सेकण्ड
3 किमी पत्थर	300 सेकण्ड
4 किमी पत्थर	400 सेकण्ड
5 किमी पत्थर	500 सेकण्ड

इन प्रेक्षणों के द्वारा ग्राफ खींचने पर चित्र 8.31 के समान ग्राफ प्राप्त होता है।

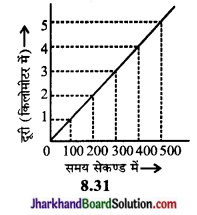
इस ग्राफ से स्पष्ट है कि दूरी व समय के बीच एक सीधी रेखा प्राप्त हुई है अतः कार की गति एकसमान गति है दूरी समय आलेख का ढाल (झुकाव ) वस्तु की चाल को प्रदर्शित करता है।

असमान गति- यदि किसी वस्तु द्वारा समान समय अन्तरालों में तय की गयी दूरियाँ असमान हों तो वस्तु की गति असमान गति कहलाती है।

उदाहरण के लिए यदि कोई कार असमान चाल से चल रही है तो कार द्वारा समान समय अन्तरालों में तय की गयी दूरियाँ भिन्न-भिन्न होंगी।

समय	दूरी
0 सेकण्ड में	0 मीटर
1 सेकण्ड में	6 मीटर
2 सेकण्ड में	14 मीटर
3 सेकण्ड में	21 मीटर
4 सेकण्ड में	30 मीटर
5 सेकण्ड में	40 मीटर

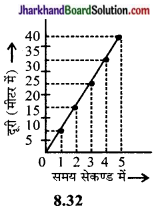
चित्र से स्पष्ट है कि कार द्वारा समान समय अन्तरालों में तय की गयी दूरी समान नहीं है अतः यह गति असमान गति है। इसे त्वरित गति भी कहते हैं।

प्रश्न 2.
हम किसी वस्तु की स्थिति कैसे निरूपित करते हैं?
उत्तर:
किसी वस्तु की स्थिति निरूपित करने के लिए आवश्यक है-
(i) एक नियत बिन्दु जिसे ‘मूल’ अथवा ‘निर्देश बिन्दु’ कहते हैं।

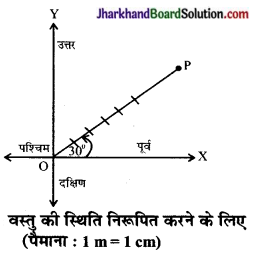
(ii) एक ‘निश्चित रेखा’ जो कि मूल बिन्दु से होकर जाती है और जिसे ‘सन्दर्भ अक्ष’ भी कहते हैं। अतः किसी वस्तु की स्थिति को व्यक्त करने के लिए आवश्यक है-

• वस्तु की मूल बिन्दु 0 से दूरी तथा
• ‘सन्दर्भ अक्ष’ और वस्तु एवं मूल बिन्दु को मिलाने वाली रेखा के बीच स्थित कोण

चित्र 8.33 में एक वस्तु की स्थिति बिन्दु P पर है जो कि मूल बिन्दु पर 6 मीटर दूर उत्तर:पूर्व दिशा में है।

प्रश्न 3.
अदिश राशि क्या है? उदाहरण दीजिए।
उत्तर:
अदिश राशि – वे भौतिक राशियाँ जिनको व्यक्त करने के लिए केवल परिमाण की आवश्यकता होती है, अदिश राशि कहलाती हैं। दूरी, चाल, समय, क्षेत्रफल आदि अदिश राशियाँ हैं।

प्रश्न 4.
सदिश राशियाँ क्या हैं? उदाहरण दीजिए।
उत्तर:
वे भौतिक राशियाँ जिनको दर्शाने के लिए दिशा तथा परिमाण दोनों की आवश्यकता होती है, ‘सदिश राशियाँ’ कहलाती हैं। विस्थापन, वेग, बल आदि सदिश राशियाँ हैं।

प्रश्न 5.
निम्नलिखित में से अदिश तथा सदिश राशियाँ छाँटो-
तापक्रम, संहति, आयतन चाल, विस्थापन, समय, दूरी, वेग, विद्युत आवेश, त्वरण, बल, संवेग, कार्य भार तथा ऊर्जा, घनत्व।
उत्तर:

• अदिश- तापक्रम, संहति, आयतन, चाल, समय, दूरी, विद्युत आवेश, घनत्व, कार्य और ऊर्जा।
• सदिश – विस्थापन, वेग, त्वरण, बल, संवेग तथा भार।

प्रश्न 6.
चलन या गमन क्या है? जीव-जन्तुओं में कौन-कौन सी गति देखी जा सकती है? उदाहरण दो।
उत्तर:
जीव-जन्तुओं की गतिशीलता को चलन या गमन कहते हैं। जीव-जन्तुओं की निम्नलिखित गतियाँ होती हैं-

• हाथी अथवा गाय जैसे जन्तु, अपने पैरों के द्वारा एक स्थान से दूसरे स्थान तक जाते हैं।
• जन्तु एक स्थान पर स्थिर रहते हुए भी अपने अंगों, जैसे- कान, पूँछ, सिर को हिला सकते हैं।
• साँप, छिपकली जैसे जन्तु रेंगते हुए एक स्थान से दूसरे स्थान तक जाते हैं।
• तितली हवा में उड़ती है और मछली पानी में तैरती है।

प्रश्न 7.
जीव-जन्तुओं की तुलना में पेड़-पौधों की गति स्वाभाविक क्यों नहीं होती? पेड़-पौधों की गति के उदाहरण दो।
उत्तर:
जीव-जन्तुओं की तुलना में पेड़-पौधों की गति का प्रेक्षण सरलता से नहीं किया जा सकता क्योंकि कुछ ही पेड़-पौधे बहुत धीमी गति से गतिशील होते हैं। जैसे-

• पौधे की जड़ें मिट्टी में नीचे की ओर तथा उसकी कोंपलें ऊपर की ओर गति करती हैं।
• पेड़ की पत्तियाँ और नई शाखाएँ निरन्तर उत्पन्न होती और बढ़ती रहती हैं।
• फूलों के खिलने तथा फलों के बढ़ने के कारण भी गति होती है।

प्रश्न 8.
सजीव एवं निर्जीव वस्तुओं की गतियों में क्या अन्तर है?
उत्तर:
पेड़-पौधों तथा जीव-जन्तुओं में गति स्वत: ही होती है अर्थात् उनकी गति स्वतः गति है। लेकिन निर्जीव वस्तुओं में गति के लिए किसी बाह्य कारक की आवश्यकता होती है। जैसे- पंखे को चलाने के लिए विद्युत की आवश्यकता होती है और स्कूटर को गति देने के लिए पेट्रोल की आवश्यकता होती है।

प्रश्न 9.
गणितीय विधि से एकसमान त्वरण के अन्तर्गत ऋजुरेखीय गति करती किसी वस्तु के लिए गति के समीकरणों का निगमन कीजिए।
उत्तर:
गणितीय विधि द्वारा गति के समीकरण स्थापित करना
(i) गति का प्रथम समीकरण माना, किसी गतिशील वस्तु का प्रारम्भिक वेग 1 व एकसमान त्वरण है। माना सेकण्ड में दूरी चलने के पश्चात् वस्तु का वेग हो जाता है, तब
1 सेकण्ड में वस्तु के वेग में वृद्धि = a
t सेकण्ड में वस्तु के वेग में वृद्धि = a x t
अतः t सेकण्ड पश्चात् वस्तु का वेग प्रारम्भिक वेग + t सेकण्ड में वस्तु के वेग वृद्धि
या v = u + at

(ii) गति का द्वितीय समीकरण-माना, किसी गतिशील वस्तु का प्रारम्भिक वेग u तथा एकसमान त्वरण a है माना, t समय पश्चात् वस्तु का अन्तिम वेग हो जाता है; अतः
1 सेकण्ड में वस्तु के वेग में वृद्धि = a
गति के प्रारम्भ होने के 1 सेकण्ड बाद वस्तु का वेग = (u + a)
गति समाप्त होने के 1 सेकण्ड पहले वस्तु का वेग =(v – a)
अतः वस्तु का औसत वेग = \(\frac{(u+a)(v-a)}{2}=\left(\frac{u+v}{2}\right)\)
इसी प्रकार, गति प्रारम्भ होने के 2 सेकण्ड बाद वस्तु का वेग = (u+2a)
गति समाप्त होने के 2 सेकण्ड पहले वस्तु का वेग = (v – 2a )
अतः वस्तु का औसत वेग = \(\frac{(u+2 a)(v-2 a)}{2}\)
= \(\frac { u+v }{ 2 }\)
इस प्रकार, त्वरण के नियत होने पर वस्तु का औसत वेग सदैव ही \(\frac { 1 }{ 2 }\) (M+ v) रहता है अतः हम यह मान सकते हैं कि सेकण्ड तक वस्तु इसी औसत वेग \(\frac { 1 }{ 2 }\) (M + v) से चलती रही है।
अत: t सेकण्ड में वस्तु द्वारा चली गई दूरी,
s = वस्तु का औसत वेग x समय = \(\frac { 1 }{ 2 }\) (u + v) × t
परन्तु गति के प्रथम समीकरण v = u + at से,
अतः वस्तु द्वारा चली गई दूरी 5 = \(\frac { u+u+at }{ 2 }\) x t
= \(\frac{2 u t+a t^2}{2}\)
s = at + \(\frac { 1 }{ 2 }\)at²

(iii) गति का तृतीय समीकरण गति के प्रथम समीकरण v = u + at का दोनों ओर का वर्ग करने पर,
v² = (u + at)² = u² + 2u at + a² t²
= u² + 2a (ut + \(\frac { 1 }{ 2 }\)at²)
परन्तु गति के द्वितीय समीकरण ut + \(\frac { 1 }{ 2 }\)at² = s से,
v² = u² + 2 as

प्रश्न 10.
चाल- समय ग्राफ से किसी वस्तु द्वारा चली गई दूरी किस प्रकार ज्ञात करोगे?
उत्तर:
चाल-समय ग्राफ से किसी वस्तु द्वारा चली गई दूरी ज्ञात करना – यदि समय को X- अक्ष पर तथा चाल को Y-अक्ष पर लेकर ग्राफ खींचा जाए तो इसे वस्तु का चाल – समय ग्राफ कहते हैं। इस ग्राफ से हम किसी भी समयान्तराल में वस्तु द्वारा चली गई दूरी ज्ञात कर सकते हैं।

यदि वस्तु की चाल नियत है तो समय-चाल ग्राफ चाल – समय के समान्तर एक सरल रेखा होगी चित्र – 8.34)।
यदि ∆t = (t₂ – t₁ ) समय में वस्तु द्वारा चली गई दूरी ∆s (s₂ – s₁) है तो

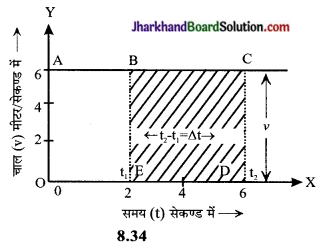
वस्तु की चाल (v) = \(\frac { ∆ s }{ ∆ t }\)
अतः वस्तु द्वारा चली गई दूरी
(∆s) = v = ∆t = DC × ED
= 6 x (6 – 2) सेकण्ड
= 6 x 4 मीटर
= 24 मीटर
इस प्रकार, किसी गतिमान वस्तु द्वारा तय की गई दूरी, उसके चाल – समय ग्राफ तथा समय-अक्ष के बीच घिरे क्षेत्रफल के बराबर होती है। यह तथ्य एकसमान गति तथा असमान गति दोनों के लिए समान रूप से लागू होता है।

प्रश्न 11.
निम्नलिखित के समय वेग ग्राफ खींचकर उदाहरण द्वारा समझाइए – (i) एकसमान वेग, (ii) एकसमान त्वरित गति (iii) असमान त्वरित गति।

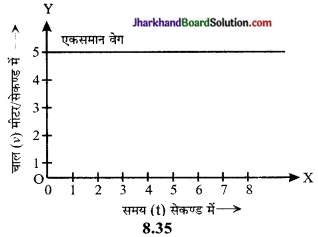
उत्तर:
(i) एकसमान वेग-यदि कोई वस्तु एक नियत दिशा में इस प्रकार गति करती है कि उसके द्वारा समान समयान्तरालों में तय की गई दूरियाँ समान हैं, तब वस्तु का वेग, एकसमान वेग कहलाता है। चित्र 8.35 में एक वस्तु का वेग – समय ग्राफ प्रदर्शित है। जिसमें कोई वस्तु 5 मीटर / सेकण्ड के समान वेग से एक निश्चित दिशा में चल रही है। यह ग्राफ समय अक्ष के समान्तर एक सरल रेखा है, जो यह दर्शाती है कि वस्तु का वेग सदैव 5 मीटर / सेकण्ड बना रहता है। इस प्रकार एकसमान वेग से गतिमान वस्तु का समय- वेग ग्राफ, समय अक्ष के समान्तर सरल रेखा के रूप में होता है।

(ii) एकसमान त्वरित गति यदि किसी वस्तु के वेग में समान समयान्तरालों में समान परिवर्तन होता है तो वस्तु की गति एकसमान त्वरित गति कहलाती है। चित्र 8.36 में मुक्त रूप से गिरते हुए पत्थर का वेग समय ग्राफ प्रदर्शित है।

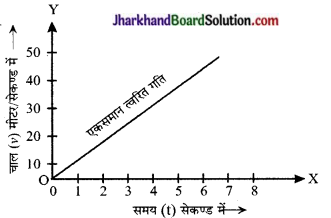
इसमें पत्थर का वेग प्रति सेकण्ड 9.8 मीटर / सेकण्ड बढ़ता रहता है, अर्थात् वस्तु की गति में त्वरण 9.8 मीटर / सेकण्ड² है। यह ग्राफ एक झुकी हुई सरल रेखा के रूप में प्राप्त होता है, जो दर्शाता है कि वस्तु की गति, एकसमान त्वरित गति है।

(iii) असमान त्वरित गति – यदि किसी वस्तु के वेग में समान समयान्तरालों में असमान परिवर्तन होते हैं, तब वस्तु की गति असमान त्वरित गति कहलाती है। चित्र 8.37 में किसी शहर में एक कार की गति का वेग समय ग्राफ दिया गया है। इसमें कार का वेग घटता बढ़ता है। यह ग्राफ टेढ़े-

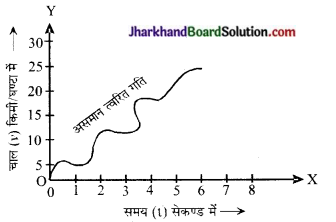
मेढ़े वक्र के रूप में प्राप्त होता है, जो यह दर्शाता है कि कार की गति असमान त्वरित गति है।

प्रश्न 12.
वेग- समय ग्राफ से त्वरण ज्ञात करने की विधि उदाहरण सहित समझाइए।
उत्तर:
वेग-समय ग्राफ से त्वरण ज्ञात करना – चित्र 8.38 में किसी वस्तु का वेग समय ग्राफ दिखाया गया है। ग्राफ से स्पष्ट है कि वेग समान दर बढ़ रहा है।

किसी वस्तु का त्वरण ज्ञात करने के दो बिन्दु A व B लेते हैं। माना A पर t₁ समय पर वेग v₁ तथा बिन्दु B पर t₂ समय पर वेग v₂ है।
अतः

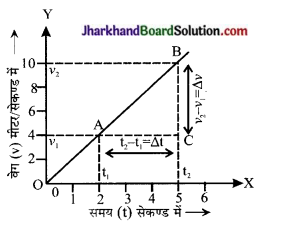
वेग परिवर्तन = v₂ – v₁ = BC
तथा समयान्तराल = t₂ – t₁ = AC

इस प्रकार, किसी गतिमान वस्तु का त्वरण, उनके वेग-समय ग्राफ के ढाल के बराबर होता है।

आंकिक प्रश्न

प्रश्न 1.
कोई कार एकसमान रूप से त्वरित होकर 5 सेकण्ड में 18 किमी / घण्टा से 36 किमी / घण्टा की गति प्राप्त करती है। ज्ञात कीजिए-
(i) त्वरण
(ii) उतने समय में कार द्वारा तय दूरी।
हल:
दिया है u = 18 किमी / घण्टा
= 18 × \(\frac {5}{18}\)
= 5 मीटर/सेकण्ड
v = 36 किमी / घण्टा = 36 × \(\frac {5}{18}\) = 10 मीटर / सेकण्ड
t = 5 सेकण्ड, a = ?. s = ?
(i) त्वरण a = \(\frac{v-u}{t}=\frac{10-5}{5}=\frac{5}{5}\) = 1 मीटर/सेकण्डर

(ii) तय दूरी v² – u² = 2as से,
अतः तय दूरी s = \(\frac{100-25}{2}=\frac{75}{2}\) = 37.5 मीटर।

प्रश्न 2.
किसी कार पर ब्रेक लगाने से वह गति की विपरीत दिशा में 6 मीटर/सेकण्ड’ का त्वरण उत्पन्न करती है। यदि कार ब्रेक लगाये जाने के बाद रुकने में 2 सेकण्ड का समय लेती है तो उतने समय में तय की गई दूरी की गणना कीजिए ।
हल:
दिया है a = -6 मीटर / सेकण्ड², रुकने पर v = 0 तथा t = 2 सेकण्ड
माना कि ब्रेक लगाने के समय कार का वेग u है तो
सूत्र v = u + at से, 0 = u + (-6) × 2
या u = 6 × 2 = 12 मीटर / सेकण्ड
अब इस बीच तय दूरी
s = ut+ \(\frac {1}{2}\) at² = 12 × 2 + \(\frac {1}{2}\) (-6) × 2²
= 24 – 3 × 4 – 12
अतः रुकने तक कार 12 मीटर की दूरी तय करती है।

प्रश्न 3.
कोई वस्तु 2 मीटर/सेकण्ड के वेग से 5 सेकण्ड तक चलती है। अगले 5 सेकण्ड में एकसमान त्वरण के कारण उसका वेग बढ़कर 10 मीटर / सेकण्ड हो जाता है। इसके बाद इस वस्तु का वेग एकसमान रूप से कम होता है। और वस्तु 10 सेकण्ड में विराम अवस्था में आ जाती है तो
(a) इस वस्तु की गति के लिए वेग समय तथा दूरी – समय ग्राफ खींचिए।
(b) ग्राफ में वह भाग दिखाइए जहाँ गति एकसमान है तथा जहाँ असमान है।
(c) ग्राफ से वस्तु द्वारा प्रारम्भ से 2 सेकण्ड बाद, 12 सेकण्ड बाद तथा अन्तिम 10 सेकण्ड में तय की गई दूरी ज्ञात कीजिए।
हल:
(a) वेग-समय ग्राफ –
पैमाना – समय-अक्ष, 1 सेमी = 2 सेकण्ड
वेग- अक्ष, 1 सेमी = 2 मीटर / सेकण्ड

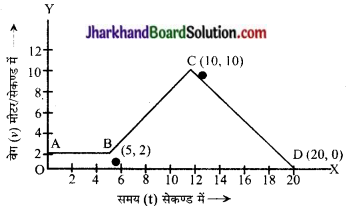
प्रथम 5 सेकण्ड में वस्तु का वेग अचर 2 मीटर / सेकण्ड है; अत: t = 0 सेकण्ड से t = 5 सेकण्ड तक ग्राफ समय अक्ष के समान्तर सरल रेखा होगी जो वेग अक्ष को 2 मीटर / सेकण्ड पर काटता है। t = 5 सेकण्ड से t = 10 सेकण्ड के बीच वेग 2 मीटर/सेकण्ड से एकसमान त्वरण से बढ़कर 10 मीटर / सेकण्ड हो जाता है। अतः यहाँ ग्राफ बिन्दुओं B (5, 2) तथा C ( 10, 10) को मिलाने वाली सरल रेखा होगी। तीसरे भाग में ग्राफ बिन्दुओं C ( 10, 10) तथा D (20,0 ) को मिलाने वाली सरल रेखा होगी।

दूरी – समय ग्राफ – दूरी – समय ग्राफ खींचने के लिए सर्वप्रथम हमें विभिन्न समयों पर वस्तु द्वारा तय की गई दूरियाँ ज्ञात करनी होंगी।
प्रथम भाग में, पहले 5 सेकण्ड के लिए वस्तु का वेग 2 मीटर / सेकण्ड है; अतः इस भाग में तय दूरी,
S₁ = vt = 2 मीटर/सेकण्ड x 5 सेकण्ड = 10 मीटर
अतः t = 5 सेकण्ड पर s = 10 मीटर।
अगले 5 सेकण्ड की गति के लिए, प्रारम्भिक वेग u = 2 मीटर / सेकण्ड v = 10 मीटर / सेकण्ड = 5 सेकण्ड।
समीकरण v = u + at से,
त्वरण a = \(\frac{v-u}{t}=\frac{10-2}{5}=\frac{8}{5}\)
a = 1.6 मीटर / सेकण्ड²
समीकरण s = ut + \(\frac {1}{2}\) at² से,
इस दौरान तय दूरी –
s = 2 × 5 + \(\frac {1}{2}\) x 1.6 (5)² = 10 + 20 = 30 मीटर
∴ प्रथम 10 से. में तय दूरी s = प्रथम 5 से. में तय दूरी + 30 = 10 + 30 = 40 मीटर
अतः इस भाग के लिये = 5 + 5 = 10 से. पर s = 40 मी.
अन्तिम 10 से. की गति लिये, प्रारम्भिक वेग u = 10 मी / से. v = 0 t = 10, सेकण्ड; v = u + at से
इस भाग का त्वरणं a = \(\frac{v-u}{t}=\frac{0-10}{10}\) = -1 मी / से²
समी. s = ut + \(\frac {1}{2}\) at² से
s = 10 × 10 + \(\frac {1}{2}\) (-1) × 10² = 100 – 50 = 50 मीटर
∴ 20 सेकण्ड में तय कुल दूरी = 40 + 50 = 90 मीटर
अतः अन्तिम भाग के लिए t=10 + 10 = 20 सेकण्ड पर 90 मीटर।
इस प्रकार हमें निम्न सारणी प्राप्त होती है –

समय (सेकण्ड में)	0	5	10	20
दूरी s (मीटर में)	0	10	40	90

उपर्युक्त आँकड़ों के आधार पर वस्तु का दूरी-ग्राफ नीचे दिया गया है।

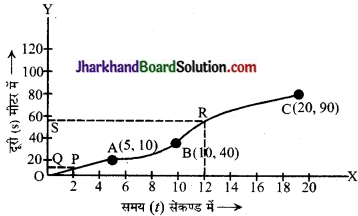
पैमाना –
समय – अक्ष 1 सेमी = 2 सेकण्ड
दूरी – अक्ष 1 सेमी = 20 मीटर
वेग- समय ग्राम में, भाग AB एकसमान गति को तथा भाग BC व CD असमान गति को प्रदर्शित करते हैं।

(b) दूरी-वेग समय ग्राफ में, भाग OA एकसमान गति को तथा भाग AB व BC असमान गति को प्रदर्शित करते हैं।

(c) दूरी – समय – ग्राफ से, 12 सेकण्ड बाद तय दूरी के लिए t = 2 सेकण्ड पर समय- अक्ष के लम्बवत् रेखा खींची जो ग्राफ को बिन्दु P पर काटती है। बिन्दु P से दूरी-अक्ष के लम्बवत् रेखा खींची जो दूरी-अक्ष को बिन्दु Q पर काटती है। बिन्दु Q के संगत दूरी अक्ष पर दूरी = 4 मीटर।
∴ t = 2 सेकण्ड बाद तय दूरी = 4 मीटर ।
इसी प्रकार, = 12 सेकण्ड बाद तय दूरी = 58 मीटर।
इसी प्रकार, प्रथम 10 सेकण्ड में तय दूरी = 40 मीटर (बिन्दु B)
तथा कुल 20 सेकण्ड में तय दूरी = 90 मीटर ( बिन्दु C )
∴ अन्तिम 10 सेकण्ड में तय दूरी = 90 मीटर 40 मीटर = 50 मीटर ।

प्रश्न 4.
संलग्न चित्र – 8.41 में प्रदर्शित चाल – समय ग्राफ से ज्ञात कीजिए –
(i) वस्तु की प्रारम्भिक चाल
(ii) 6 सेकण्ड में वस्तु द्वारा चली गई दूरी
(iii) वस्तु का त्वरण।

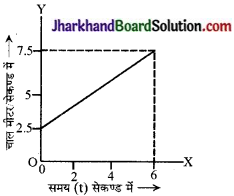
हल:
(i) वस्तु की प्रारम्भिक चाल = 2.5 मीटर/सेकण्ड ।

(ii) 6 सेकण्ड में वस्तु द्वारा चली गई दूरी = चाल × समय
= (7.5 – 2.5 ) मीटर / सेकण्ड × 6 सेकण्ड
= 5 × 6 मीटर = 30 मीटर

\(\frac {5}{6}\) मीटर/सेकण्ड²
= 0.83 मीटर / सेकण्ड² ।

प्रश्न 5.
संलग्न चित्र 8.42 में किसी गतिशील पिण्ड का वेग-समय ग्राफ प्रदर्शित है। ज्ञात कीजिए –
(i) प्रथम 10 सेकण्ड में चली गई दूरी
(ii) 15वें सेकण्ड पर पिण्ड का त्वरण
(iii) 20 से 25 सेकण्ड के बीच त्वरण।

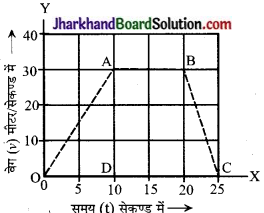
हल:
(i) प्रथम 10 सेकण्ड में चली गई दूरी
= समकोण ∆OAD का क्षेत्रफल
= \(\frac {1}{2}\) × OD × AD
= \(\frac {1}{2}\) × (10 – 0) सेकण्ड × (30 × 0) मीटर/सेकण्ड = 150 मीटर।
(ii) 15वें सेकण्ड पर त्वरण शून्य होगा; क्योंकि वेग – परिवर्तन शून्य है।

(iii) 20 से 25 सेकण्ड के बीच त्वरण

= – \(\frac {30}{5}\)
= – 6 मीटर / सेकण्ड² ।

प्रश्न 6.
कोई जलयान 56 किलोमीटर/घण्टा की चाल से चल रहा है। 1 सेकण्ड के पश्चात् उसकी चाल 58 किलोमीटर / घण्टा हो जाती है। उसका त्वरण ज्ञात कीजिए।
हल:
दिया है : जलयान का प्रारम्भिक वेग (4) = 56 किलोमीटर/घण्टा,
जलयान का अन्तिम वेग (v) = 58 किलोमीटर/घण्टा
समय (t) = 1 सेकण्ड = \(\frac {1}{3600}\) घण्टा
जलयान का त्वरण (a) =

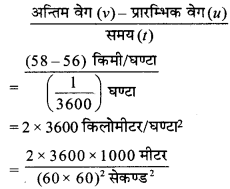
=  \(\frac {5}{9}\)मीटर / सेकण्ड²
= 0.56 मीटर / सेकण्ड²

प्रश्न 7.
10 सेकण्ड में एक कार का वेग 36 किमी / घण्टा से 72 किमी/घण्टा हो जाता है। कार का त्वरण ज्ञात कीजिए।
हल:
दिया है कार प्रारिम्भक वेग (u) = 36 किमी / घण्टा
= \(\frac{36 \times 1000}{60 \times 60}\) मीटर/सेकण्ड
= 10 मीटर / सेकण्ड
तथा कार का अन्तिम वेग (v) = 72 किमी / घण्टा
= \(\frac{72 \times 1000}{60 \times 60}\)
= 20 ‘मीटर/सेकण्ड
अतः कार का त्वरण (a) =

= 1 मीटर / सेकण्ड²

प्रश्न 8.
एक गोली 90 मीटर / सेकण्ड के वेग से लक्ष्य से टकराकर 0.3 सेकण्ड में रुक जाती है। गोली का मन्दन ज्ञात कीजिए।
हल:
दिया है : u = 90 मीटर / सेकण्ड, v = 0, t = 0.3 सेकण्ड a = ?
समीकरण v = u + at से,
0 = 90 + a × 0.3
अतः गोली का मन्दन (a) = – \(\frac{90}{0.3}\)
= – 300 मीटर / सेकण्ड²।