Jharkhand Board JAC Class 9 Maths Important Questions Chapter 5 युक्लिड के ज्यामिति का परिचय Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 5 युक्लिड के ज्यामिति का परिचय
प्रश्न 1.
यदि दो रेखाएँ परस्पर लम्बवत् हों, तो उनके मध्य कोण होगा :
(A) 180°
(B) 80°
(C) 90°
(D) 360°
हल :
दो लम्बवत् रेखाओं के मध्य कोण 90° होता है।
अतः सही विकल्प ‘C’ है।
![]()
प्रश्न 2.
रेखाखण्ड की लम्बाई होती है :
(A) अनिश्चित दूरी
(B) निश्चित दूरी
(C) अपनी इच्छा के अनुरूप
(D) किन्हीं दो बिन्दुओं के मध्य दूरी।
हल :
किन्हीं दो बिन्दुओं के मध्य की दूरी को रेखाखण्ड द्वारा व्यक्त किया जाता है। होगी:
अतः सही विकल्प ‘D’ है।
प्रश्न 3.
दो बिन्दुओं से गुजरने वाली रेखाओं की संख्या
(A) एक
(B) तीन
(C) अनन्त
(D) दो।
हल :
दो बिन्दुओं से होकर केवल एक रेखा गुजर सकती है।
अतः सही विकल्प ‘A’ है।
प्रश्न 4.
यदि रेखाखण्ड AB तथा CD बराबर तथा संपाती हैं और यदि CD = 3 सेमी हो, तो AB की दूरी दोगुनी हो जाने पर CD की दूरी हो जायेगी :
(A) 1.5 सेमी
(B) 6 सेमी
(C) 5 सेमी
(D) 9 सेमी।
हल :
AB = CD (दिया है)
CD = 3 सेमी
यदि AB दोगुनी कर दी जाय, तो CD भुजा भी दोगुनी होगी।
∴ CD = 3 × 2 = 6 सेमी ।
अतः सही विकल्प ‘B’ है।
![]()
प्रश्न 5.
यदि एक रेखा दो समान्तर रेखाओं को काटती है तो उसके एक ही ओर बने दो अन्तः कोणों का योग होगा :
(A) 180° से कम
(B) 2 समकोण
(C) 180° से अधिक
(D) 180° < 90°.
हल :
दो समान्तर रेखाओं को कोई एक तिर्यक रेखा काटती है, तो उससे बने अन्तः कोणों का योग 2 समकोण अर्थात् 180° होता है।
अतः सही विकल्प ‘B’ है।
प्रश्न 6.
यूक्लिड ने सांत रेखा किसे कहा था ?
(A) किरण को
(B) रेखा को
(C) रेखाखण्ड को
(D) त्रिज्या को।
हल :
यूक्लिड ने रेखाखण्ड को सांत रेखा कहा था।
अतः सही विकल्प ‘C’ है।
प्रश्न 7.
अथर्ववेद में दिये गये ‘श्रीयंत्र’ में एक-दूसरे से जुड़े कितने समद्विबाहु त्रिभुज अन्तर्निहित हैं :
(A) आठ
(B) छ:
(C) नौ
(D) पन्द्रह ।
हल :
‘श्रीयन्त्र’ में एक-दूसरे से जुड़े ‘नौ’ समद्विबाहु त्रिभुज अन्तर्निहित हैं।
अतः सही विकल्प ‘C’ है।
![]()
प्रश्न 8.
एलीमेन्ट्स (Elements) नामक प्रसिद्ध ग्रन्थ के लेखक हैं :
(A) गणितज्ञ थेल्स
(B) गणितज्ञ यूक्लिड
(C) गणितज्ञ पाइथागोरस
(D) गणितज्ञ आर्यभट्ट |
हल :
एलीमेन्ट्स नामक प्रसिद्ध ग्रन्थ के लेखक गणितज्ञ यूक्लिड थे।
अतः सही विकल्प ‘B’ है।
प्रश्न 9.
ज्यामितीय विधि से \(\sqrt{3}\), \(\sqrt{5}\) ………. आदि को अपरिमेय सिद्ध करने वाले गणितज्ञ थे :
(A) थिरोडोरस
(B) बोधायन
(C) आर्काइटस
(D) बेल्स
हल :
ज्यामितीय विधि से \(\sqrt{3}\), \(\sqrt{5}\) ………. आदि को अपरिमेय सिद्ध करने वाले गणितज्ञ थिरोडोरस थे ।
अतः सही विकल्प ‘A’ है।
प्रश्न 10.
यूनानियों ने ज्यामिति का ज्ञान प्राप्त किया था :
(A) भारत से
(B) अमेरिका से
(C) मिस्त्र से
(D) इंग्लैण्ड से
हल :
यूनानियों ने ज्यामिति का ज्ञान मिस्त्र से प्राप्त किया था।
अतः सही विकल्प ‘C’ है।
![]()
प्रश्न 11.
वे वस्तुएँ जो एक ही वस्तु के बराबर हों, एक दूसरे के ………….. ‘होती हैं।
हल :
बराबर ।
प्रश्न 12.
एक सांत रेखा को …………….. रूप से बढ़ाया जा सकता है।
हल :
अनिश्चित ।
प्रश्न 13.
उस भारतीय गणितज्ञ का नाम बताइए जो पाइथागोरस प्रमेय की खोज पहले ही कर चुके थे।
हल :
पाइथागोरस प्रमेय की खोज करने वाले सर्वप्रथम गणितज्ञ बोधायन थे।
प्रश्न 14.
क्या समान्तर रेखाएँ, किसी बिन्दु पर प्रतिच्छेद करती हैं ? यदि नहीं तो क्यों ?
हल :
नहीं, क्योंकि समान्तर रेखाओं के मध्य की दूरी सदैव समान होती है, इसलिए वे प्रतिच्छेद नहीं कर सकती।
![]()
प्रश्न 15.
यूक्लिड ने ज्यामिति के कौन-कौन से मुख्य बिन्दुओं को अपने शब्दों में परिभाषित किया है ?
हल :
यूक्लिड ने बिन्दु, रेखा और तल को अपने शब्दों में परिभाषित किया है।
प्रश्न 16.
ज्यामिति में गणितज्ञों ने कौन-कौन से पदों को अपरिभाषित माना है?
हल :
- बिन्दु – इसका कोई परिमाण नहीं होता है।
- रेखा – सीधी रेखा को दोनों ओर कितना भी बढ़ाया जा सकता है।
- तल – दीवार का समतल पृष्ठ, समतल भूमि, कागज का पृष्ठ तल आदि ।
प्रश्न 17.
दो बिन्दुओं से कितनी रेखाएँ गुजर सकती हैं ?
हल :
दो बिन्दुओं से केवल एक रेखा गुजर सकती है।
![]()
प्रश्न 18.
यूक्लिड द्वारा दी गई अभिधारणाओं में से कोई दो अभिधारणाएँ लिखिए।
हल :
अभिधारणा (1) – एक बिन्दु से अन्य बिन्दु तक एक सीधी रेखा खींची जा सकती है।
अभिधारणा (2) – किसी बिन्दु को केन्द्र मानकर भिन्न त्रिज्याओं वाले अनन्त वृत्त खींचे जा सकते हैं।
प्रश्न 19.
सिद्ध कीजिए कि एक दिये हुए रेखाखण्ड पर एक समबाहु त्रिभुज की रचना की जा सकती है।.
हल :
प्रश्नानुसार,
(i) बिन्दु A को केन्द्र मानकर AB त्रिज्या का वृत्त खींचते हैं।
(ii) इसी प्रकार बिन्दु B को केन्द्र मानकर BA त्रिज्या लेकर दूसरा वृत्त खींचते हैं ये दोनों वृत्त C बिन्दु पर मिलते हैं।
(iii) बिन्दु C से A और B बिन्दु को मिलाते हैं।
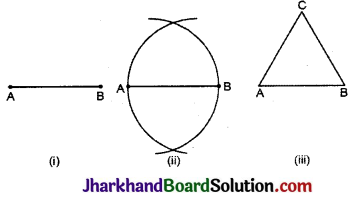
इस प्रकार ΔABC की चना हुई।
जहाँ AB = AC, क्योंकि ये एक ही वृत्त की त्रिज्याएँ हैं।
इस प्रकार, AB = BC (एक ही वृत्त की त्रिज्याएँ)
⇒ AB = BC = AC
अत: ΔABC समबाहु त्रिभुज है।
![]()
प्रश्न 20.
यदि A, B और C एक रेखा पर स्थित तीन बिन्दु हैं और B बिन्दुओं A और C के बीच स्थित है, तो सिद्ध कीजिए कि AB + BC = AC.
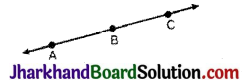
हल :
चित्र में, AB + BC के साथ AC सम्पाती है।
हम जानते हैं कि वे वस्तुएँ जो परस्पर संपाती हों एक- दूसरे के बराबर होती हैं।
अतः AB + BC = AC.
अतः दो बिन्दुओं से होकर एक अद्वितीय रेखा खींची जा सकती है।
प्रश्न 21.
यूक्लिड ने ज्यामिति के बिन्दु, रेखा और तल (पृष्ठ) के बारे में क्या परिभाषाएँ दीं हैं, लिखिए।
हल :
- बिन्दु ऐसी आकृति होती है, जिसका कोई भाग नहीं होता।
- रेखा की केवल लम्बाई होती है, चौड़ाई नहीं
- एक सीधी रेखा ऐसी रेखा है जो स्वयं पर बिन्दुओं के साथ सपाट रूप में स्थित होती है।
- एक पृष्ठ वह है जिसकी लम्बाई चौड़ाई होती है।
- किसी पृष्ठ के किनारे रेखाएँ होती हैं।
- एक समतल पृष्ठ ऐसा पृष्ठ है जो स्वयं पर सीधी रेखाओं के साथ सपाट रूप से स्थित होता है।