Jharkhand Board JAC Class 9 Maths Important Questions Chapter 8 चतुर्भुज Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 8 चतुर्भुज
प्रश्न 1.
यदि किसी चतुर्भुज की चारों भुजाएँ और कोण परस्पर बराबर हों, तब चतुर्भुज होगा :
(A) आयत
(B) समचतुर्भुज
(C) वर्ग
(D) समान्तर चतुर्भुज ।
हल :
विकल्प (C) सही है।
![]()
प्रश्न 2.
यदि समान्तर चतुर्भुज के दो विकर्ण समान हों, तो यह होगा :
(A) चतुर्भुज
(B) आयत
(C) समचतुर्भुज
(D) समलम्ब चतुर्भुज ।
हल :
विकल्प (B) सही है।
प्रश्न 3.
चित्र में ABCD एक समचतुर्भुज है। यदि AC = 8 सेमी और DB = 6 सेमी हो, तो BC का मान होगा :
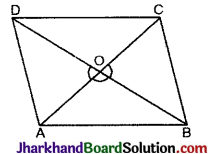
(A) 5 सेमी
(B) 4 सेमी
(C) 7 सेमी
(D) 3.5 सेमी
हल :
हम जानते हैं कि समचतुर्भुज के विकर्ण एक दूसरे को 90° पर समद्विभाजित करते हैं, तब ΔOBC में,
OC = \(\frac {1}{2}\)AC = \(\frac {1}{2}\) × 8 = 4 सेमी
OB = \(\frac {1}{2}\) × BD = \(\frac {1}{2}\) × 6 = 3 सेमी
पाइथागोरस प्रमेय से,
BC2 = OB2 + OC2 = 32 + 42
= 9 + 16 = 25
BC = 5 सेमी।
अतः विकल्प ‘A’ सही है।
![]()
प्रश्न 4.
त्रिभुज की दो भुजाओं के मध्य बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समान्तर तथा लम्बाई में उसका होता है
(A) आधा
(B) बराबर
(C) एक-तिहाई
(D) एक-चौथाई
हल :
विकल्प (A) सही है।
प्रश्न 5.
किसी चतुर्भुज में सम्मुख भुजाओं का एक युग्म परस्पर समान्तर है, चतुर्भुज होगा :
(A) समलम्ब
(B) आयत
(C) वर्ग
(D) समचतुर्भुज
हल :
विकल्प (B) सही है।
प्रश्न 6.
यदि किसी चतुर्भुज के विकर्ण बराबर हो तथा एक दूसरे को समकोण पर प्रतिच्छेदित करते हों, तो वह होगा :
(A) आयत
(B) वर्ग
(C) समचतुर्भुज
(D) समान्तर चतुर्भुज
हल :
विकल्प (B) सही है।
प्रश्न 7.
यदि किसी चतुर्भुज के विकर्ण असमान हैं तथा एक-दूसरे को समकोण पर समद्विभाजित करते हों तो वह होगा :
(A) आयत
(B) वर्ग
(C) समचतुर्भुज
(D) समान्तर चतुर्भुज
हल :
विकल्प (C) सही है।
प्रश्न 8.
समान्तर चतुर्भुज ABCD में ∠A = 75° हो, तो ∠B का मान है :
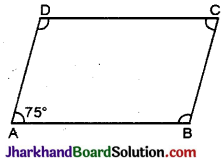
(A) 105°
(B) 110°
(C) 90°
(D) 75°.
हल :
∠A + ∠B = 180° (अन्तः कोण)
⇒ 75° + ∠B = 180°
∴ ∠B = 180° – 75° = 105°.
अतः विकल्प ‘A’ सही है।
![]()
प्रश्न 9.
वर्ग की भुजा एवं उसके विकर्ण की लम्बाइयों का अनुपात है:
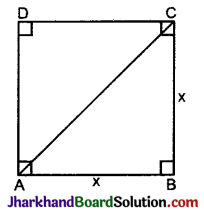
(A) 1 : \(\sqrt{2}\)
(B) 3 : \(\sqrt{2}\)
(C) \(\sqrt{2}\) : 1
(D) \(\sqrt{2}\) : 3
हल :
AC2 = AB2 + BC2
= x2 + x2 = 2x2
∴ AC = \(\sqrt{2}\)x
∴ AB : AC = x : \(\sqrt{2}\)x
= 1 : \(\sqrt{2}\)
अतः विकल्प ‘A’ सही है।
प्रश्न 10.
चित्र में, ABCD समान्तर चतुर्भुज है, तो x का मान होगा:
(A) 25°
(B) 60°
(C) 75°
(D) 45°.
हल :
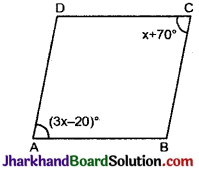
हम जानते हैं कि
∠A = ∠C
3x – 20° = x + 70°
या 2x = 90°
∴ x = 45°
(3x-20)
अतः विकल्प ‘D’ सही है।
प्रश्न 11.
रिक्त स्थानों की पूर्ति करो :
(i) किसी ||gm के विकर्ण एक दूसरे को ……………………. करते हैं।
(ii) समान्तर चतुर्भुज के संलग्न कोण होते हैं।
(iii) किसी ||gm के सम्मुख कोण ………………. होते हैं।
(iv) किसी ||gm की सम्मुख भुजाएँ …………………… होती हैं।
(v) किसी चतुर्भुज की भुजाओं के मध्य बिन्दुओं को एक क्रम से मिलाने वाले रेखाखण्डों द्वारा बना चतुर्भुज ………………. होता है।
(vi) किसी समान्तर चतुर्भुज का एक कोण समकोण हो तो वह ………………….. कहलाता है।
(vii) किसी त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के …………………. होती है।
(viii) पतंग एक ……………….. चतुर्भुज नहीं है।
संलग्न चित्र को ध्यान से देखिए
(ix) …………. समान्तर रेखाएँ हैं।
(x) …………. समान रेखाएँ हैं।
(xi) समान कोणों के नाम हैं ………………।
(xii) सम्पूरक कोणों के नाम है ………………।
हल :
(i) समद्विभाजित,
(ii) सम्पूरक,
(iii) बराबर,
(iv) समान,
(v) समान्तर चतुर्भुज,
(vi) आयत,
(vii) समान्तर तथा आधी,
(viii) समान्तर
(ix) AB || DC तथा AD || BC,
(x) AB = DC तथा AD = BC,
(xi) ∠A = ∠C तथा ∠B = ∠D
(xii) ∠A व ∠B, ∠B व ∠C, ∠C व ∠D, तथा ∠D व ∠A.
![]()
प्रश्न 12.
ΔABC में, D, E, F क्रमश: भुजाओं AB, BC और CA के मध्य बिन्दु हैं। सिद्ध कीजिए कि बिन्दुओं D, E,F को मिलाने पर ABC चार सर्वांगसम त्रिभुजों में विभाजित हो जाता है।
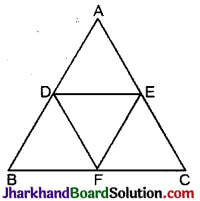
हल :
ΔABC में, बिन्दु D, E तथा F क्रमश: भुजाओं AB, AC तथा BC के मध्य बिन्दु ।
रचना: DE, EF तथा DF को मिलाया।
सिद्ध करना है ΔADE ≅ ΔDBF ≅ ΔEFC ≅ ΔDEF
∵ D और E क्रमश: भुजा AB व BC के मध्य बिन्दु है।
∴ DE || BC
इसी प्रकार DF || AC
और EF || AB है।
∴ ADEF, BDFE और DFCE समान्तर चतुर्भुज
∵ समान्तर चतुर्भुज BDFE में DF विकर्ण है।
∴ ΔBDF ≅ ΔFED
(∵ समान्तर चतुर्भुज को विकर्ण दो बराबर सर्वांगसम त्रिभुजों में बाँटता है)
इसी प्रकार ΔDAE ≅ ΔFED
और ΔEFC ≅ ΔFED
ΔADE ≅ ΔDBF ≅ ΔEFC ≅ ΔDEF इति सिद्धम् ।
प्रश्न 13.
D, E व F एक ΔABC की भुजा BC, AC AB के मध्य बिन्दु है। सिद्ध कीजिए कि AD, भुजा EF का समद्विभाजक है।
हल :
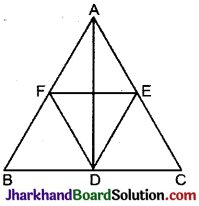
दिया है ΔABC
में, D, E व F क्रमश: BC, AC व AB के मध्य बिन्दु हैं।
सिद्ध करना है AD, EF को समद्विभाजित करता है।
रचना: DE, EF तथा DF को मिलाया ।
उपपत्ति: D व E क्रमश: BC व AC के मध्य बिन्दु (दिया है)
∴ DE || AB अथवा DE || AF ……..(i)
इसी प्रकार D व F क्रमश: BC व AB के मध्य बिन्दु (दिया है)
∴ DF || AC अथवा DF || AE ……….(ii)
(i) व (ii) से,
AEDF एक समान्तर चतुर्भुज है।
∵ समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं और AD व EF समान्तर चतुर्भुज AEDF के विकर्ण हैं।
∴ AD, EF को समद्विभाजित करता है। इति सिद्धम् ।
![]()
प्रश्न 14.
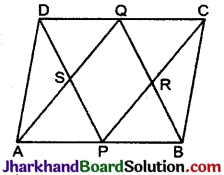
ABCD एक समचतुर्भुज है और P, Q, R, S क्रमश: AB, BC, CD तथा DA के मध्य बिन्दु हैं। सिद्ध कीजिए कि PQRS एक आयत है।
हल :
दिया है : समचतुर्भुज ABCD में P, Q, R, व S क्रमश: AB, BC, CD व DA के मध्य बिन्दु हैं।
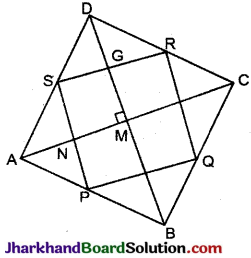
सिद्ध करना है : PQRS एक आयत हैं।
रचना : विकर्ण AC तथा BD खींचे।
उपपत्ति: ΔABC में P एवं Q क्रमश: AB तथा BC के मध्य बिन्दु हैं। (दिया है)
∴ PQ || AC ……..(i)
तथा PQ = \(\frac {1}{2}\)AC ……..(ii)
इसी प्रकार ΔADC में,
SR || AC ……..(iii)
तथा SR = \(\frac {1}{2}\)AC ……..(iv)
∴ समीकरण (i) एवं (iii) से.
PQ || SR ……..(v)
पुन: समीकरण (ii) तथा (iv) सं.
PQ = SR ……..(vi)
∴ समीकरण (v) व (vi) से,
PQRS एक समान्तर चतुर्भुज हैं। ………(vii)
पुनः SR || AC ….(iii) से
∴ SG = MN …..(viii)
इसी प्रकार ΔABP में,
∴ SP || DB
SN || GM ……..(ix)
समीकरण (viii) तथा (ix) से,
SNMG एक समान्तर चतुर्भुज है
∴ ∠GMN = ∠GSN
(||gm के सम्मुख कोण) … (x)
किन्तु समचतुर्भुज के विकर्ण समकोण पर काटते हैं
∴ ∠GMN = 90° ……….. (xi)
समीकरण (x) व (xi) से,
∠GSN = ∠RSP = 90° ………. (xii)
∴ समीकरण (vii) व (xii) से,
PQRS एक आयत है। इति सिद्धम् ।
![]()
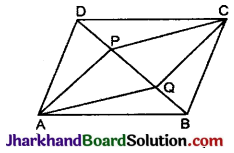
प्रश्न 15.
चित्र में ABCD एक समान्तर चतुर्भुज है। P और Q क्रमशः सम्मुख भुजाओं AB और CD के मध्य- बिन्दु हैं। सिद्ध कीजिए कि PRQS एक समान्तर चतुर्भुज है।
हल :
दिया है : समान्तर चतुर्भुज ABCD में AB और CD के मध्य बिन्दु क्रमश: P और Q हैं।
सिद्ध करना है :
PQRS एक समान्तर चतुर्भुज है।
उपपत्ति: चूँकि P और Q क्रमश: AB और CD के मध्य- बिन्दु हैं।
∴ AP = \(\frac {1}{2}\)AB
और CQ = \(\frac {1}{2}\)CD ……….(i)
लेकिन AB = CD
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
⇒ \(\frac {1}{2}\)AB = \(\frac {1}{2}\)CD
⇒ AP = CQ ……….(ii)
और AB || DC
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
⇒ AP || CQ ……….(iii)
इस प्रकार चतुर्भुज APCQ में,
AP || CQ और APCQ [समीकरण (ii) और (iii) से]
⇒ APCQ एक समान्तर चतुर्भुज है। ………..(iv)
इसी प्रकार BPDQ एक समान्तर चतुर्भुज है। ……..(v)
अब समीकरण (iv) से,
AQ || PC ⇒ SQ || RP ……. (vi)
समीकरण (v) से,
BQ || PD ⇒ RQ || PS … (vii)
समी. (vi) व (vii) से,
SPRQ एक समान्तर चतुर्भुज है। इति सिद्धम् ।
प्रश्न 16.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC । AD, बहिष्कोण PAC को समद्विभाजित करता है और CD || BA दर्शाइए कि :
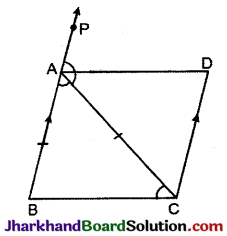
(i) ∠DAC = ∠BCA
(ii) ABCD एक समान्तर चतुर्भुज है।
हल :
दिया है : समद्विबाहु ΔABC में AB = AC, तथा बहिष्कोण PAC का समद्विभाजक AD.
रचना : AD = BC काटी DC को मिलाया
सिद्ध करना है : (i) ∠DAC = ∠BCA
(ii) ABCD एक समान्तर चतुर्भुज है।
उपपत्ति:
(i) ABC समद्विबाहु त्रिभुज है, जिसमें
AB = AC (दिया है)
∴ ∠ABC = ∠ACB ……..(1)
(समान भुजाओं के सम्मुख कोण)
बहिष्कोण ∠PAC = ∠ABC + ∠ACB ……….(2)
समीकरण (1) और (2) से,
∠PAC = 2∠ACB ………..(3)
∵ AD, कोण ∠PAC को समद्विभाजित करती है।
∴ ∠PAC = 2∠DAC …….(4)
समीकरण (3) व (4) से,
2∠DAC = 2∠ACB
∠DAC = ∠ACB. इति सिद्धम् ।
(ii) ∠DAC = ∠ACB (एकान्तर कोण)
रेखाखण्ड BC और AD को तिर्यक रेखा AC काटती है।
∴ BC || AD
और BA || CD (दिया है)
अत: ABCD समान्तर चतुर्भुज है। इति सिद्धम् ।
![]()
प्रश्न 17.
एक चतुर्भुज ABCD के विकर्ण परस्पर लम्ब हैं। सिद्ध कीजिए कि इनकी भुजाओं के मध्य बिन्दुओं को मिलाने वाले रेखाखण्डों से एक आयत बनता है।
हल :
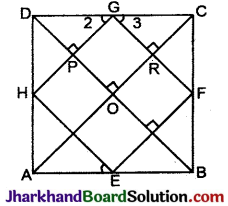
दिया है चतुर्भुज ABCD के विकर्ण AC व BD इस प्रकार है कि AC ⊥ BD तथा E, F, G H क्रमश: AB, BC, CD व AD के मध्य बिन्दु हैं। P तथा Q क्रमश: भुजाओं GH व GF के मध्य बिन्दु हैं।
सिद्ध करना है : EFGH एक आयत है।
उपपत्ति: ΔADC में, G व H क्रमश: CD तथा AD के मध्य बिन्दु है। (दिया है)
∴ GH || AC व GH = \(\frac {1}{2}\)AC ……(i)
पुन: ΔABC में,
E व F क्रमश: AB तथा BC के मध्य बिन्दु हैं। (दिया है)
∴ EF || AC एवं EF = \(\frac {1}{2}\)AC ……(ii)
समीकरण (i) व (ii) से,
GH || EF तथा GH = EF … (iii)
चतुर्भुज EFGH की सम्मुख भुजाएँ बराबर व परस्पर समान्तर हैं।
∴ EFGH एक समान्तर चतुर्भुज है।
इसी प्रकार GF || DB
तथा GH || AC
∴ ORGP एक समान्तर चतुर्भुज है, जिसका ∠POR = 90°
∴ ∠PGR = ∠POR = 90° (||gm के सम्मुख कोण)
∴ GHEF एक आयत है। इति सिद्धम् ।
प्रश्न 18.
समान्तर चतुर्भुज ABCD में विकर्ण BD पर दो बिन्दु P और Q इस प्रकार स्थित हैं कि DP = BQ । सिद्ध कीजिए कि APCQ एक समान्तर चतुर्भुज है।
हल :
दिया है समान्तर चतुर्भुज ABCD के विकर्ण BD पर दो बिन्दु P और Q इस प्रकार हैं कि
DP = BQ
सिद्ध करना है: APCQ एक समान्तर चतुर्भुज है।
उपपत्ति: ΔAPD और ΔCQB में,
AD = BC
(समान्तर चतुर्भुज की सम्मुख भुजाएँ)
∠ADP = ∠CBQ (एकान्तर कोण)
DP = BQ. (दिया है)
ΔAPD ≅ ΔCQB
अर्थात् (SAS नियम)
AP = CQ ……….(1)
इसी प्रकार ΔCPD और ΔAQB में, हम सिद्ध कर सकते हैं कि
CP = AQ ……….(2)
समीकरण (1) और (2) से,
APCQ एक समान्तर चतुर्भुज है। इति सिद्धम् ।
![]()
प्रश्न 19.
सिद्ध कीजिए कि त्रिभुज की एक भुजा के मध्य- बिन्दु से, एक अन्य भुजा के समान्तर खींची गई रेखा, तीसरी भुजा को उसके मध्य बिन्दु पर प्रतिच्छेदित करती है।
हल :
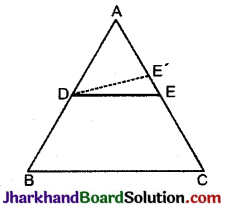
दिया है त्रिभुज ABC में, AB का मध्य बिन्दु D है। D से BC के समान्तर खींची गई रेखा त्रिभुज की भुजा AC
को बिन्दु E पर प्रतिच्छेदित करती है।
सिद्ध करना है E, AC का मध्य- बिन्दु है। रचना AE पर कोई बिन्दु E किया तथा D और E को मिलाया ।
उपपत्ति : मान लीजिए E, भुजा AC का मध्य-बिन्दु नहीं है, और मान लीजिए कि E, भुजा AC का मध्य- बिन्दु है।
अब त्रिभुज ABC में, D, AB का मध्यबिन्दु है, और E’, AC का मध्य-बिन्दु है।
∴ DE’ || BC ……..(1)
परन्तु DE || BC (दिया है) …….. (2)
समीकरण (1) और (2) से स्पष्ट है कि दो प्रतिच्छेदी रेखाएँ DE और DE’ दोनों रेखा BC के समान्तर हैं।
परन्तु यह तो अंतर्विरोध है।
इस प्रकार हमारी कल्पना गलत है।
अतः AE = EC
अर्थात् E, AC का मध्य बिन्दु है। इति सिद्धम् ।
प्रश्न 20.
समान्तर चतुर्भुज ABCD के विकर्ण BD पर A और C से डाले गये लम्ब क्रमश: AP तथा CQ हैं।
सिद्ध कीजिए कि AP = CQ.
हल :
सिद्ध करना है:
AP = CQ
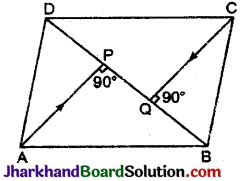
उपपत्ति: विकर्ण समान्तर चतुर्भुज को दो समान क्षेत्रफल वाले त्रिभुजों में बाँटता है।
∴ ΔABD का क्षेत्रफल = ΔBDC का क्षेत्रफल
त्रिभुज का क्षे. = \(\frac {1}{2}\) × आधार × ऊँचाई
∴ \(\frac {1}{2}\)BD × AP = \(\frac {1}{2}\)BD × CQ
∴ AP = CQ.
![]()
प्रश्न 21.
दी गई आकृति में, D, E और F क्रमशः भुजाओं BC, CA तथा AB के मध्य बिन्दु हैं। यदि, AB = 4.3 सेमी, BC = 5.6 सेमी, और AC = 3.9 सेमी हैं तो निम्नलिखित का परिमाप ज्ञात कीजिए: (i) ΔDEF और (ii) चतुर्भुज BDEF
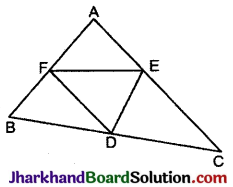
हल :
(i) त्रिभुज की किन्ही दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड सम्मुख भुजा का आधा होता है।
अतः ΔDEF में,
DE = \(\frac {1}{2}\)AB
EF = \(\frac {1}{2}\)BC
DF = \(\frac {1}{2}\)AC
∴ ΔDEF का परिमाप = DE + EF + DF
= \(\frac {1}{2}\)AB + \(\frac {1}{2}\)BC + \(\frac {1}{2}\)AC
= \(\frac {1}{2}\)(AB + BC + AC)
= \(\frac {1}{2}\)(4.3 + 5.6 + 3.9)
= \(\frac {1}{2}\)(13.8)
= 6.9 सेमी।
(ii) चतुर्भुज BDEF का परिमाप
= BD + DE + EF + BF
= \(\frac {1}{2}\)BC + \(\frac {1}{2}\)AB + \(\frac {1}{2}\)BC + \(\frac {1}{2}\)AB
= AB + BC
= 4.3 + 5.6
= 9.9 सेमी।
प्रश्न 22.
ΔABC का ∠B समकोण है और P, भुजा AC का मध्य बिन्दु है। सिद्ध कीजिए कि PB = PA = \(\frac {1}{2}\)AC
हल :
दिया है ΔABC में, ∠B = 90° व P, AC का मध्य बिन्दु है।
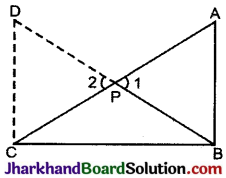
सिद्ध करना है PB = PA = \(\frac {1}{2}\)AC
रचना: PC पर एक ΔPDC बनाया जिसमें PB = PD
उपपत्ति : ΔAPB व ΔCPD में,
PA = PC (दिया है)
∠1 = ∠2 (शीर्षभिमुख कोण)
PB = PD (रचना से)
∴ ΔAPB ≅ ΔCPD (SAS नियम)
∴ AB = CD ……(i)
तथा ∠BAP = ∠DCP
किन्तु ये एकान्तर कोण हैं
∴ AB || CD ………..(i)
पुन: ∠ABC + ∠DCB = 180°
किन्तु ∠ABC = 90°
∴ ∠DCB = 90° ………..(ii)
पुन: ΔMBC व ΔDCB में,
BC = BC (उभयनिष्ठ)
∠ABC = ∠DCB (प्रत्येक 90°)
AB = CD ((i) से)
∴ ΔABC ≅ ΔDCB (SAS नियम)
तब AC = BD
⇒ \(\frac {1}{2}\)AC = \(\frac {1}{2}\)BD
किन्तु \(\frac {1}{2}\)AC = AP
तथा \(\frac {1}{2}\)BD = BP
∴ PB = PA = \(\frac {1}{2}\)AC.
इति सिद्धम् ।
![]()
प्रश्न 23.
त्रिभुज ABC में, भुजा AB को M और N तीन बराबर भागों में बाँटते हैं। दोनों रेखाखण्ड MP और NQ भुजा BC के समान्तर हैं और AC को क्रमश: P और Q पर मिलते हैं। सिद्ध कीजिए कि P और Q भुजा AC को भी तीन बराबर भागों में बाँटते हैं।
हल :
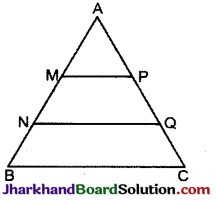
दिया है ΔABC में,
AM = MN = NB
उपपत्ति: क्योंकि MP || BC व NQ || BC
∴ MP || NQ || BC …(i)
AB व AC, MP, NO एवं BC को क्रमश: M, N
तथा P व O पर इस प्रकार काटती है कि
MN = NB (दिया है)
PQ = QC …(ii)
पुन: M, AN का मध्य बिन्दु है,
तथा MP || NQ [(i) से]
∴ AP = NQ ….(iii)
अब (ii) तथा (iii) से
AP = PQ = QC इति सिद्धम् ।
प्रश्न 24.
सिद्ध कीजिए कि त्रिभुज की माध्यिका उसको समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।
हल :
दिया है त्रिभुज ABC में AD भुजा BC की माध्यिका है।
सिद्ध करना है:
ΔABD का क्षेत्रफल = ΔACD का क्षेत्रफल
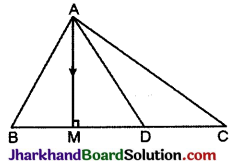
रचना: शीर्ष A से सम्मुख भुजा BC पर AM लम्ब को डाला।
उपपत्ति: ΔABC में AD माध्यिका है।
∵ BD = CD ……(i)
∴ त्रिभुज ABD तथा त्रिभुज ADC के आधार एक ही रेखा BC (CD) पर होने और दोनों त्रिभुजों के एक ही शीर्ष A होने से AM दोनों त्रिभुजों की ऊँचाई है।
∴ ΔABD का क्षेत्रफल | क्षेत्रफल = \(\frac {1}{2}\)BD × AM
ΔACD का क्षेत्रफल = \(\frac {1}{2}\)CD × AM
परन्तु, BD = CD [समीकरण (i) से]
∴ ΔABD का क्षेत्रफल = ΔACD का क्षेत्रफल
इति सिद्धम्