JAC Class 9 Maths Important Questions Chapter 11 रचनाएँ

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 11 रचनाएँ Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 11 रचनाएँ

प्रश्न 1.
एक त्रिभुज ABC की रचना कीजिए जिसमें ∠B = 45°, ∠C = 60° और A से BC पर लम्ब AD = 4 सेमी।
हल :
दिया है ΔABC में, ∠B = 45°, ∠C = 60° तथा शीर्ष लम्ब AD = 4 सेमी।

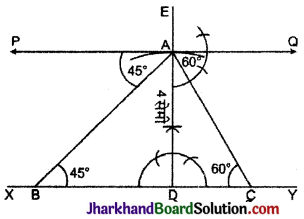
रचना :

1. सर्वप्रथम XY रेखाखण्ड खींचा।
2. XY रेखाखण्ड पर कोई बिन्दु D लिया।
3. D से ED ⊥ XY खींचा।
4. AD = 4 सेमी काटा।
5. A बिन्दु से XY के समान्तर PQ खींची।
6. XY के बिन्दु A पर क्रमश: ∠PAB = 45° और ∠QAC = 60° के कोण बनाती हुई रेखाएँ खींची जो XY को B तथा C बिन्दुओं पर मिलती हैं।
7. इस प्रकार प्राप्त ΔABC ही अभीष्ट त्रिभुज है।

प्रश्न 2.
त्रिभुज ABC की रचना कीजिए, जिसकी परिमिति 12 सेमी एवं आधार कोण 50° और 70° हों।
हल :

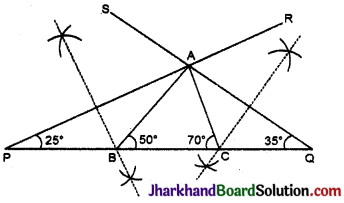
रचना :

1. सर्वप्रथम PQ = 12 सेमी का रेखाखण्ड खींचा।
2. PQ के बिन्दु P से कोण RPQ = \(\frac {50°}{2}\) = 25° बनाती हुई रेखा PR खींची तथा PQ के बिन्दु Q से कोण SQP = \(\frac {70°}{2}\) = 35° का कोण बनाती हुई QS रेखा खींची जो परस्पर A बिन्दु पर काटती है।
3. AP और AQ के लम्ब समद्विभाजक खींचे जो PQ को क्रमश: B और C बिन्दुओं पर मिलते हैं।
4. A को B व C को 4 से मिलाया।
5. इस प्रकार प्राप्त त्रिभुज ABC ही अभीष्ट त्रिभुज है, जिसमें AB + BC + CA = 12 सेमी है।

प्रश्न 3.
त्रिभुज ABC की रचना कीजिए जिसमें BC = 6 सेमी, AB – AC = 2 सेमी और ∠C = 30° हो ।
हल :

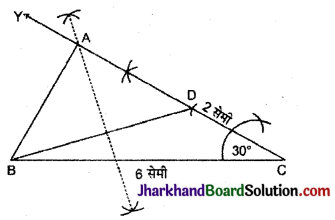
रचना :

1. रेखा BC = 6 सेमी की खींची।
2. बिन्दु C पर 30° का कोण बनाती हुयी रेखा CY खींचा।
3. CY में से CD = 2 सेमी काटा।
4. BD को मिलाया।
5. BD का लम्ब समद्विभाजक खींचा जो CY की A बिन्दु पर काटता है।
6. AB को मिलाया।
   अतः अभीष्ट त्रिभुज ABC प्राप्त हुआ।

प्रश्न 4.
त्रिभुज PQR की रचना कीजिए, जिसमें RQ = 6 सेमी, ∠Q = 60° और PQ + PR = 8 सेमी है।
हल :

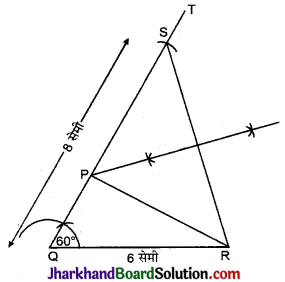
रचना :

1. सर्वप्रथम भुजा RQ = 6 सेमी की खींची।
2. भुजा RQ के बिन्दु Q पर 60° का कोण बनाती हुयी रेखा QT खींची।
3. QT से QS = (PQ + PR = 8 सेमी) काटा।
4. S को R से मिलाया।
5. RS का लम्ब समद्विभाजक खींचा जो SQ को बिन्दु P पर काटता है।
6. P को R से मिलाया।
   ΔPQR ही अभीष्ट त्रिभुज है जिसमें PQ + PR = 8 सेमी है।

प्रश्न 5.
त्रिभुज ABC की रचना कीजिए, जिसमें AB = 4 सेमी, AC = 3 सेमी और भुजा BC पर शीर्ष लम्ब 2.5 सेमी लम्बा हो ।
हल :
रचना :
1. सर्वप्रथम XY रेखा खींची।
2. XY रेखाखण्ड पर कोई बिन्दु D लिया उस पर PD लम्ब खींचा।
3. PD में से AD = 2.5 सेमी काटा।

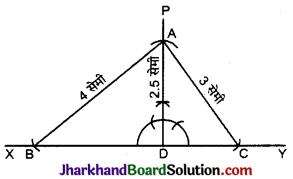
4. A को केन्द्र मानकर क्रमशः 4 सेमी और 3 सेमी की त्रिज्या लेकर चाप लगाये जो XY को क्रमश: B और C बिन्दुओं पर काटते हैं।
5. A को B और C को 4 से मिलाया।
6. प्राप्त ΔABC ही अभीष्ट त्रिभुज है।

प्रश्न 6.
त्रिभुज ABC की रचना कीजिए जिसमें AB = AC = 8 सेमी, ∠A = 75°, ∠B का समद्विभाजक खींचिए जो सामने की भुजा को मिले।
हल :
रचना :
1. भुजा AB = 8.0 सेमी की खींची।
2. बिन्दु A पर 75° का कोण बनाती हुयी AX रेखा खींची तथा AC = 8 सेमी काटा।
3. बिन्दु A को केन्द्र मानकर 8.0 सेमी त्रिज्या का एक चाप लगाया जो RA को C पर काटता है।

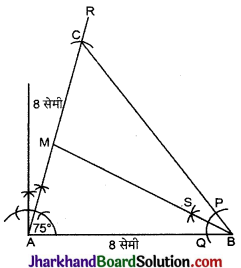
4. C को B से मिलाया।
5. B को केन्द्र मानकर किसी भी त्रिज्या का एक चाप PQ लगाया जो AB और BC को क्रमश: Q और P बिन्दुओं पर काटता है।
6. अब P और Q को केन्द्र मानकर दो चाप खींचे जो एक-दूसरे को S बिन्दु पर काटते हैं।
7. B और S को मिलाती हुयी रेखा खींची जो AC को M पर मिलती है।
8. इस प्रकार बना त्रिभुज AMB ही अभीष्ट त्रिभुज है।

प्रश्न 7.
ΔABC की रचना कीजिए जिसमें a = 7 सेमी, b = 5 सेमी और c = 4 सेमी। A से BC पर लम्ब डालिए ।
हल :
दिया है ΔABC में a = 7 सेमी, b = 5 सेमी और c = 4 सेमी अर्थात् BC = 7 सेमी, AC = 5 सेमी, AB = 4 सेमी।
रचना :
1. सर्वप्रथम रेखाखण्ड BC = 7 सेमी खींचा।
2. B को केन्द्र मानकर 4 सेमी त्रिज्या से तथा C को केन्द्र मान कर 5 सेमी की त्रिज्या से चाप लगाए जो परस्पर A बिन्दु पर काटते हैं।

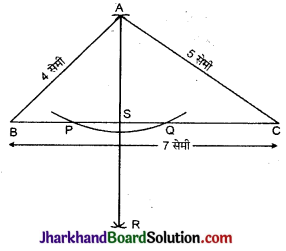
3. A को B से व C को A से मिलाया। यही अभीष्ट त्रिभुज ABC है।
4. अब बिन्दु A को केन्द्र मानकर चाप खींचा जो BC को क्रमश: P और Q बिन्दुओं पर काटता है।
5. P और Q को क्रमशः केन्द्र मानकर तथा उचित त्रिज्या से दो चाप BC के नीचे की ओर खींचे जो एक-दूसरे को R बिन्दु पर काटते हैं।
6. A को R से मिलाया, जो BC भुजा को S पर काटता है।
7. अत: AS, ही A से BC पर खींचा गया अभीष्ट लम्ब है।