JAC Class 9 Maths Important Questions Chapter 12 हीरोन का सूत्र

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 12 हीरोन का सूत्र Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 12 हीरोन का सूत्र

प्रश्न 1.
एक त्रिभुज की भुजाएँ 40 सेमी, 70 सेमी एवं 90 सेमी हैं । त्रिभुज का क्षेत्रफल होगा :
(A) 600\(\sqrt{5}\) वर्ग सेमी
(B) 500\(\sqrt{6}\) वर्ग सेमी
(C) 482\(\sqrt{5}\) वर्ग सेमी
(D) 60\(\sqrt{5}\) वर्ग सेमी
हल :
यहाँ a = 40 सेमी, b = 70 सेमी, c = 90 सेमी
अर्द्ध-परिमाप (s) = \(\frac{a+b+c}{2}=\frac{40+70+90}{2}\)
= \(\frac {200}{2}\) = 100 सेमी

प्रश्न 2.
एक समबाहु त्रिभुज की भुजा 6 सेमी है। त्रिभुज का क्षेत्रफल होगा :
(A) 6\(\sqrt{3}\) वर्ग सेमी
(B) 9\(\sqrt{3}\) वर्ग सेमी
(C) 16\(\sqrt{3}\) वर्ग सेमी
(D) 3\(\sqrt{3}\) वर्ग सेमी
हल :
हम जानते हैं कि
समबाहु त्रिभुज का क्षेत्रफल = \(\frac{a^2 \sqrt{3}}{4}\), जहाँ ‘a’ भुजा है।
= \(\frac{(6)^2 \sqrt{3}}{4}=\frac{36 \sqrt{3}}{4}\)
= 9\(\sqrt{3}\) वर्ग सेमी
अतः विकल्प (B) सही है।

प्रश्न 3.
एक समकोण त्रिभुज का क्षेत्रफल 36 वर्ग सेमी है एवं आधार 9 सेमी है, तो इसके लम्ब की लम्बाई होगी :
(A) 8 सेमी
(B) 4 सेमी
(C) 16 सेमी
(D) 32 सेमी
हल :
त्रिभुज का क्षेत्रफल = \(\frac {1}{2}\) × आधार × लम्ब
⇒ 36 = \(\frac {1}{2}\) × 9 × लम्ब
⇒ 36 × 2 = 9 × लम्ब
∴ लम्ब = \(\frac{36 \times 2}{9}\)
= 4 × 2 = 8 सेमी
अत: सही विकल्प (A) है।

प्रश्न 4.
एक समान्तर चतुर्भुज का क्षेत्रफल 96 सेमी² एवं ऊँचाई 8 सेमी हो तो आधार होगा :
(A) 9.7 सेमी
(B) 8 सेमी
(C) 14 सेमी
(D) 12 सेमी
हल :
समान्तर चतुर्भुज का क्षेत्रपफल आधार ऊँचाई = आधार × ऊँचाई
∴ आधार = समान्तर चतुर्भुज का क्षेत्रफल / ऊँचाई
= \(\frac {96}{8}\) = 12 सेमी
अतः सही विकल्प (D) है।

प्रश्न 5.
यदि किसी समद्विबाहु त्रिभुज की समान भुजाएँ 6 सेमी एवं अन्य भुजा 8 सेमी हो, तो इसका क्षेत्रफल होगा :
(A) 8\(\sqrt{5}\) वर्ग सेमी
(B) 5\(\sqrt{8}\) वर्ग सेमी
(C) 3\(\sqrt{55}\) वर्ग सेमी
(D) 3\(\sqrt{8}\) वर्ग सेमी
हल :
समद्विबाहु त्रिभुज का क्षेत्रफल
= \(\frac {b}{4}\)\(\sqrt{4 a^2-b^2}\)
जहाँ a समान भुजा एवं b अन्य भुजा है।
समद्विबाहु त्रिभुज का क्षेत्रफल
= \(\frac {8}{4}\)\(\sqrt{4(6)^2-(8)^2}\)
= \(\frac {8}{4}\)\(\sqrt{4 \times 36-64}\)
= 2\(\sqrt{144-64}\)
= 2\(\sqrt{80}\) = 2\(\sqrt{4 \times 4 \times 5}\)
= 2 × 4 × \(\sqrt{5}\) = 8\(\sqrt{5}\) वर्ग सेमी
अत: सही विकल्प (A) है।

प्रश्न 6.
यदि किसी समचतुर्भुज के विकर्ण 10 सेमी एवं 8 सेमी हों तो इसका क्षेत्रफल होगा :
(A) 80 वर्ग सेमी
(B) 40 वर्ग सेमी
(C) 9 वर्ग सेमी
(D) 36 वर्ग सेमी
हल :
समचतुर्भुज का क्षेत्रफल
= \(\frac {1}{2}\) × विकर्णों का गुणनफल
= \(\frac {1}{2}\) × 10 × 8
= 5 × 8 = 40 वर्ग सेमी
अत: सही विकल्प (B) है।

प्रश्न 7.
एक त्रिभुज का आधार 14 सेमी एवं ऊँचाई 10 सेमी है, तो त्रिभुज का क्षेत्रफल होगा :
(A) 240 सेमी²
(B) 60 सेमी²
(C) 70 सेमी²
(D) 140 सेमी²
हल :
त्रिभुज का क्षेत्रफल = \(\frac {1}{2}\) × आधार × ऊँचाई
= \(\frac {1}{2}\) × 14 × 10 वर्ग सेमी
= 70 वर्ग सेमी
अत: सही विकल्प (C) है।

प्रश्न 8.
यदि किसी आयत की आसन्न भुजाएँ 3 सेमी व 4 सेमी इसका विकर्ण खींचने पर बने एक त्रिभुज का अर्द्ध-परिमाप होगा :

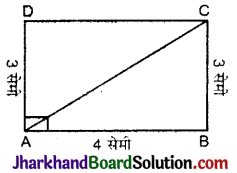
(A) 6 सेमी
(B) 10 सेमी
(C) 7 सेमी
(D) 12 सेमी।
हल :
ΔABC पाइथागोरस प्रमेय से,
AC = \(\sqrt{3^2+4^2}=\sqrt{9+16}\) = 5 सेमी
∴ ΔABC का अर्द्ध परिमाप = \(\frac{3+4+5}{2}\)
= \(\frac {12}{2}\) = 6 सेमी
अतः सही विकल्प (A) है।

प्रश्न 9.
हीरोन के सूत्र में 3 प्रकट करता है
(A) परिमाप को
(B) क्षेत्रफल को
(C) अर्द्ध परिमाप को
(D) A और B दोनों
हल :
अर्द्धपरिमाप को अत: विकल्प (C) सही है।

प्रश्न 10.
किसी अनियमित आकार के बहुभुजाकार खेत का क्षेत्रफल ज्ञात करने के लिए उसे बाँट लिया जाता है :
(A) आयतों में,
(B) वर्गों में
(C) समचतुर्भुजों में
(D) त्रिभुओं में
हल :
त्रिभुजों में, अतः विकल्प (D) सही है।

प्रश्न 11.
एक समान्तर चतुर्भुज का आधार 18 मीटर एवं क्षेत्रफल 174.60 वर्ग मीटर हो, तो इसकी ऊंचाई ज्ञात कीजिए।
हल :
समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
⇒ 174.60 = 18 × ऊँचाई
∴ ऊँचाई = \(\frac {174.60}{18}\)
= 9.7 मीटर।

प्रश्न 12.
उस समबाहु त्रिभुज की भुजा की लम्बाई ज्ञात कीजिए, जिसका क्षेत्रफल 9\(\sqrt{3}\) वर्ग सेमी है।
हल :
समबाहु त्रिभुज का क्षेत्रफल = \(\frac{a^2 \sqrt{3}}{4}\), जहाँ भुजा है।
⇒ 9\(\sqrt{3}\) = \(\frac{a^2 \sqrt{3}}{4}\)
⇒ 9 × 4\(\sqrt{3}\) = a²\(\sqrt{3}\)
⇒ a² = \(\frac{9 \times 4 \times \sqrt{3}}{\sqrt{3}}\) = 9 × 4
⇒ a² = 36
∴ a = 6 सेमी
अतः समबाहु Δ की भुजा की लम्बाई = 6 सेमी।

प्रश्न 13.
एक समद्विबाहु त्रिभुज की दो समान भुजाओं में प्रत्येक 5 सेमी एवं तीसरी भुजा 4 सेमी लम्बी है, तो त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल :
माना कि a = 5 सेमी, b = 4 सेमी
अतः समद्विबाहु त्रिभुज का क्षेत्रफल
= \(\frac {b}{4}\) × \(\sqrt{4 a^2-b^2}\)
= \(\frac {b}{4}\) × \(\sqrt{4 \times 25-16}\) वर्ग सेमी
= \(\sqrt{84}\) वर्ग सेमी
= 2\(\sqrt{21}\) वर्ग सेमी।

प्रश्न 14.
उस समबाहु त्रिभुज की ऊँचाई ज्ञात कीजिए जिसकी एक भुजा 2a है।
हल :

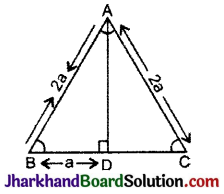
दिया है : भुजा = 2a
समबाहु त्रिभुज में शीर्ष से खींचा गया लम्ब सम्मुख भुजा को समद्विभाजित करता हैं। अत: समबाहु ΔABD में
∠ADB = 90°
AD²= AB² – BD²
(पाइथागोरस प्रमेय से)
= (2a)² – (a)²
= 4a² – a² = 3a²
AD = \(\sqrt{3}\)a इकाई
∴ त्रिभुज की ऊँचाई = \(\sqrt{3}\)a

प्रश्न 15.
एक त्रिभुजाकार खेत की भुजाएँ 20 मीटर, 51 मीटर एवं 37 मीटर हैं। 2 × 3 वर्ग मीटर माप की कितनी क्यारियाँ इस खेत में बनाई जा सकती हैं ?
हल :
त्रिभुजाकार खेत की भुजाएँ a = 20 मीटर, b = 51 मीटर, c = 37 मीटर
खेत का अर्द्ध परिमाप (s) = \(\frac{a+b+c}{2}\)
= \(\frac{20+51+37}{2}\)
= \(\frac {108}{2}\) = 54 सेमी
त्रिभुजाकार खेत का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{54(54-20)(54-51)(54-37)}\)
= \(\sqrt{54 \times 34 \times 3 \times 17}\)
= 306 वर्ग मीटर
एक क्यारी का क्षेत्रफल = 2 × 3 वर्ग मीटर
= 6 वर्ग मीटर
क्यारियों की संख्या = खेत का क्षेत्रफल / एक क्यारी का क्षेत्रफल
= 306 वर्ग मीटर / 6 वर्ग मीटर
= 51 क्यारियाँ

प्रश्न 16.
उस समबाहु त्रिभुज का क्षेत्रफल एवं ऊंचाई ज्ञात कीजिए जिसकी एक भुजा 6 सेमी हो।
हल :
माना कि एक भुजा a = 6 सेमी
समबाहु त्रिभुज का क्षेत्रफल
= \(\frac{\sqrt{3}}{4}\)a² = \(\frac{\sqrt{3}}{4}\) × (6)²
= 9\(\sqrt{3}\) वर्ग सेमी
त्रिभुज की ऊँचाई = 2 × क्षेत्रफल / आधार
= \(\frac{2 \times 9 \sqrt{3}}{6}\)
= 3\(\sqrt{3}\) सेमी
अतः त्रिभुज का क्षेत्रफल 9\(\sqrt{3}\) वर्ग सेमी एवं ऊँचाई 3\(\sqrt{3}\) सेमी है।

प्रश्न 17.
किसी समान्तर चतुर्भुज की दो आसन्न भुजाएँ क्रमश: 5 सेमी एवं 3.5 सेमी तथा विकर्ण 6.5 सेमी है। समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हल :
समान्तर चतुर्भुज का विकर्ण उसे दो बराबर क्षेत्रफल वाले त्रिभुओं में बाँटता है।
∴ समान्तर चतुर्भुज ABCD का क्षेत्रफल
= 2 × (ΔABC का क्षेत्रफल)

अतः समान्तर चतुर्भुज का क्षेत्रफल
= 2 × 5\(\sqrt{3}\) वर्ग सेमी
= 10\(\sqrt{3}\) वर्ग सेमी।

प्रश्न 18.
उस चतुर्भुज का क्षेत्रफल ज्ञात कीजिए, जिसकी भुजाएँ क्रमशः 9 सेमी, 40 सेमी, 28 सेमी एवं 15 सेमी हैं एवं प्रथम दो भुजाओं के मध्य का कोण समकोण है।
हल :
माना चतुर्भुज ABCD में भुजाएँ AB, BC, CD और DA
क्रमशः 9 सेमी, 40 सेमी, 28 सेमी और 15 सेमी हैं।
AB तथा BC के मध्य कोण 90° है।

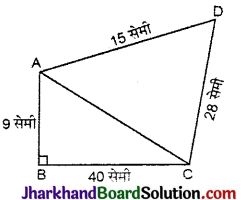
AC विकर्ण खींचा, जो चतुर्भुज ABCD को दो त्रिभुजों (ΔABC और ΔACD) में विभक्त कर देता है।
ΔABC का क्षेत्रफल
= \(\frac {1}{2}\) × (आधार × ऊँचाई )
= \(\frac {1}{2}\) × 9 × 40 = 9 × 20 = 180 वर्ग सेमी
∴ ΔABC में, पाइथागोरस प्रमेय से,
(कर्ण)² = (आधार)² + (लम्ब)²
AC² = BC² + AB²
AC² = (40)² + (9)² = 1600 + 81
AC² = 1681 वर्ग सेमी
∴ AC = \(\sqrt{1681}\) = 41 सेमी
अतः ΔACD में,
AC = 41 सेमी, CD = 28 सेमी, DA = 15 सेमी
अर्द्ध परिमाप (s) = \(\frac{41+28+15}{2}\)
= \(\frac {84}{2}\) = 42 सेमी
ΔACD का क्षेत्रफल
= \(\sqrt{42(42-41)(42-28)(42-15)}\)
= \(\sqrt{42 \times 1 \times 14 \times 27}\)
= \(\sqrt{14 \times 3 \times 14 \times 3 \times 3 \times 3}\)
= 14 × 3 × 3 = 126 वर्ग सेमी
अत: चतुर्भुज ABCD का क्षेत्रफल
= ΔABC का क्षेत्रफल + ΔACD का क्षेत्रफल
= 180 वर्ग सेमी + 126 वर्ग सेमी
= 306 वर्ग सेमी।

प्रश्न 19.
उस समलम्ब चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी समान्तर भुजाएँ क्रमशः 55 सेमी एवं 40 सेमी हैं तथा असमान्तर भुजाएँ क्रमश: 20 सेमी एवं 25 सेमी हैं।
हल :

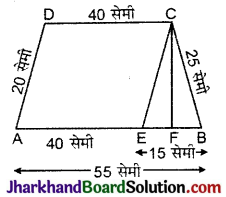
समलम्ब चतुर्भुज ABCD में समान्तर भुजाएँ AB = 55 सेमी, व DC = 40 सेमी एवं असमान्तर भुजाएँ AD = 20 सेमी एवं BC = 25 सेमी हैं। ΔBEC में,
रचना : AD || EC एवं CF ⊥ AB खींचा।
अत: EB = AB – AE = 55 – 40 = 15 सेमी एवं EC = 20 सेमी

समान्तर चतुर्भुज AECD का क्षेत्रफल
= AE × CF
= 40 × 20
= 800 वर्ग सेमी
अतः समलम्ब चतुर्भुज ABCD का क्षेत्रफल
= (स.च. AECD का क्षे.) + (ΔBEC का क्षे.)
= 800 वर्ग सेमी + 150 वर्ग सेमी
= 950 वर्ग सेमी।

प्रश्न 20.
सोनिया के पास एक खेत है जो एक समचतुर्भुज के आकार का है। वह अपनी एक पुत्री और एक पुत्र से यह चाहती थी कि वे उस खेत पर काम करके अलग-अलग फसलों का उत्पादन करें। उसने इस खेत को दो बराबर भागों में विभाजित कर दिया। यदि इस खेत का परिमाप 400 मीटर है और एक विकर्ण 160 मीटर है, तो प्रत्येक को खेती के लिए कितना क्षेत्रफल प्राप्त होगा ?
हल :
माना ABCD समचतुर्भुजाकार खेत है जिसका परिमाप 400 मीटर है। विकर्ण AC इस खेत को दो बराबर भागों में विभाजित करता है।

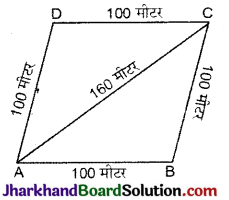
∴ प्रत्येक भुजा = \(\frac {परिमाप}{4}\) = \(\frac {400}{4}\) = 100 मीटर
विकर्ण = 160 मीटर
ΔABC का अर्द्ध परिमाप
s = \(\frac{100+100+160}{2}\)
= \(\frac {360}{2}\)
= 180 मीटर
∴ ΔABC का क्षेत्रफल
= \(\sqrt{180(180-100)(180-100)(180-160)}\)
= \(\sqrt{180 \times 80 \times 80 \times 20}\) = 4800 मीटर²
अतः प्रत्येक को खेती करने के लिए 4800 मीटर² क्षेत्रफल प्राप्त होगा।

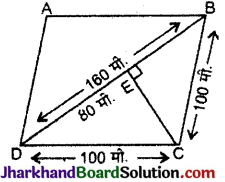
वैकल्पिक विधिः
CE ⊥ BD
∵ समद्विबा के शीर्ष से असमान भुजा पर डाला गया लम्ब उसे अद्धित करता है ।
और चूँकि विकर्ण
BD = 160 मी.
∴ DE = \(\frac {180}{2}\) = 80 मी.
अब समकोण त्रिभुज CED में
CE = \(\sqrt{(C D)^2-(D E)^2}\)
= \(\sqrt{100^2-80^2}\)
= \(\sqrt{10000-6400}\)
= \(\sqrt{3600}\)
= 60 मी.
क्षेत्रफल ΔBCD
= \(\frac {1}{2}\) × आधार × ऊँचाई
= \(\frac {1}{2}\) × 160 × 60
= 80 × 60
= 4800 मी²

प्रश्न 21.
कमला के पास 240 मीटर, 200 मीटर और 360 मीटर भुजाओं वाला एक त्रिभुजाकार खेत है, जहाँ वह गेहूँ उगाना चाहती है। इसी खेत से संलग्न 240 मीटर, 320 मीटर और 400 मीटर भुजाओं वाला एक अन्य खेत है, जहाँ वह आलू और प्याज उगाना चाहती है। उसने इस खेत की सबसे लम्बी भुजा के मध्य बिन्दु को सम्मुख शीर्ष से जोड़कर उसे दो भागों में विभाजित कर दिया। इनमें से एक भाग में उसने आलू उगाये और दूसरे भाग में प्याज उगाई गेहूँ, आलू और प्याज के लिए कितने-कितने क्षेत्रफलों (हेक्टेअर में) का प्रयोग किया गया है। (1 हेक्टेअर = 10000 वर्ग मीटर) ।
हल :
माना कि ABC वह खेत है जहाँ गेहू उगाया गया है और ACD वह खेत है जिसकी सबसे लम्बी भुजा AD के मध्य-बिन्दु E को C से जोड़कर इस खेत को दो भागों में बाँटा गया है।

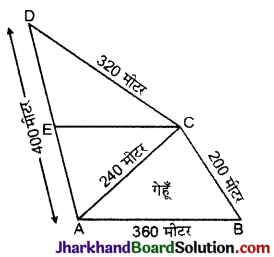
ΔABC का क्षेत्रफल :
a = 200 मीटर
b = 240 मीटर
c = 360 मीटर
s = \(\frac{200+240+360}{2}\)
s = 400 मीटर
∴ गेहूँ उगाने के लिए ΔABC का क्षेत्रफल
= \(\sqrt{400(400-200)(400-240)(400-360)}\)
= \(\sqrt{400 \times 200 \times 160 \times 40}\)
= 16000\(\sqrt{2}\) वर्ग मीटर
= 1. 6\(\sqrt{2}\) हेक्टेअर
= 1·6 × 1.414 = 2.26 हेक्टेअर (लगभग)
आलू और प्याज उगाने के लिए ΔACD का क्षेत्रफल :
s = \(\frac{240+320+400}{2}\) = 480 मीटर
ΔACD का क्षेत्रफल
= \(\sqrt{480(480-240)(480-320)(480-400)}\)
= \(\sqrt{480 \times 240 \times 160 \times 80}\)
= 38400 वर्ग मीटर
= 3.84 हेक्टेअर
CE, ΔACD की माध्यिका है। यह त्रिभुज को दो बराबर भागों में बाँटेगी।
आलू उगाने के लिए क्षेत्रफल = प्याज उगाने के लिए क्षेत्रफल
= \(\frac {3.84}{2}\)
= 1.92 हेक्टेअर
अतः गेहूँ उगाने के लिए क्षेत्रफल = 2.26 हेक्टेअर
आलू उगाने के लिए क्षेत्रफल = 1.92 हेक्टेअर
और प्याज उगाने के लिए क्षेत्रफल = 1.92 हेक्टेअर ।

प्रश्न 22.
किसी स्कूल के विद्यार्थियों ने सफाई अभियान के लिए एक रैली निकाली। उन्होंने दो समूहों में, विभिन्न गलियों में चलकर मार्च किया। एक समूह ने गलियों AB, BC और CA में मार्च किया। फिर उन्होंने इन गलियों द्वारा घेरे गये भागों को साफ किया। यदि AB = 9 मीटर, BC = 40 मीटर, CD = 15 मीटर, DA = 28 मीटर और ∠B = 90° है, तो किस समूह ने अधिक सफाई की और कितनी अधिक ? विद्यार्थियों द्वारा सफाई किया गया कुल क्षेत्रफल भी ज्ञात कीजिए।
हल :

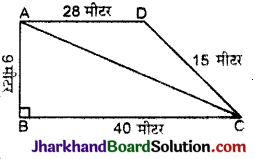
AB = 9 मीटर
BC = 40 मीटर
∠B = 90°
पाइथागोरस प्रमेय से,
AC = \(\sqrt{A B^2+B C^2}\)
= \(\sqrt{9^2+40^2}\)
= \(\sqrt{81+1600}\)
= \(\sqrt{1681}\) = 41 मीटर
पहले समूह द्वारा की गई सफाई का क्षेत्रफल
= समकोण ΔABC का क्षेत्रफल
= \(\frac {1}{2}\) × BC × AB
= \(\frac {1}{2}\) × 40 × 9
= 180 वर्ग मीटर
दूसरे समूह द्वारा की गई सफाई का क्षेत्रफल = ΔACD का क्षेत्रफल
जहाँ a = 41 मी., b = 15 मी. , c = 28 मीटर
∴ S = \(\frac{41+15+28}{2}=\frac{84}{2}\)
= 42 मीटर
ΔACD का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{42(42-41)(42-15)(42-28)}\)
= \(\sqrt{42 \times 1 \times 27 \times 14}\)
= 126 वर्ग मीटर
∴ पहले समूह ने दूसरे समूह की अपेक्षा (180 – 126) = 54 वर्ग मीटर अधिक सफाई की है।
सभी विद्यार्थियों द्वारा की गई सफाई का कुल क्षेत्रफल
= 180 + 126
= 306 वर्ग मीटर।

प्रश्न 23.
एक समबाहु त्रिभुज की माध्यिका की लम्बाई x सेमी है तो उस त्रिभुज का क्षेत्रफल ज्ञात करो ।
हल :
दिया है त्रिभुज ABC समबाहु त्रिभुज है जिसकी प्रत्येक भुजा a (माना) है।

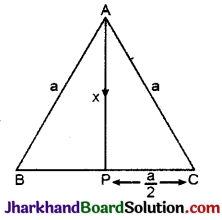
ΔAPC मैं,
AC² = AP² + PC²
a² = x² + (\(\frac {a}{2}\))²
⇒ a² = x² + \(\frac{a^2}{4}\)
⇒ a² – \(\frac{a^2}{4}\) = x²
⇒ \(\frac{3 a^2}{4}\) = x²
⇒ a² = \(\frac{4 x^2}{3}\)
⇒ a = \(\sqrt{\frac{4 x^2}{3}}\)
∴ a = \(\frac{2 x}{\sqrt{3}}\)
अब, त्रिभुज ABC का क्षेत्रफल
= \(\frac {1}{2}\) × BC × AP
= \(\frac {1}{2}\) × a × x
= \(\frac {1}{2}\) × \(\frac{2 x}{\sqrt{3}}\) × x
= \(\frac{x^2}{\sqrt{3}}\)
अतः क्षेत्रफल = \(\frac{x^2}{\sqrt{3}}\) वर्ग इकाई

प्रश्न 24.
एक त्रिभुजाकार प्लाट की भुजाओं का अनुपात 3 : 5 : 7 है तथा उसका परिमाप 300 मीटर है। इस प्लाट का क्षेत्रफल ज्ञात कीजिए।
हल :
मान लीजिए त्रिभुजाकार प्लॉट की भुजाएँ 3x, 5x तथा 7x हैं।
∴ परिमाप = 3x + 5x + 7x = 300
⇒ 15x = 300
∴ x = \(\frac {300}{15}\) = 20 मीटर
∴ प्लॉट की भुजाएँ,
a = 3 × 20 = 60 मीटर
b = 5 × 20 = 100 मीटर
c = 7 × 20 = 140 मीटर
अब, s = \(\frac{60+100+140}{2}=\frac{300}{2}\) = 150 मीटर
∴ त्रिभुज का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{150(150-60)(150-100)(150-140)}\)
= \(\sqrt{150 \times 90 \times 50 \times 10}\)
अत: क्षेत्रफल = 1500\(\sqrt{3}\) वर्ग मीटर ।

प्रश्न 25.
यदि किसी त्रिभुज की प्रत्येक भुजा को दुगुना कर दिया जाय तो इस त्रिभुज के क्षेत्रफल में कितने प्रतिशत की वृद्धि हो जायेगी।
हल :
माना कि किसी त्रिभुज की भुजाएँ क्रमश: x, y तथा z हैं एवं s इसका अर्द्ध परिमाप है। अतः
s = \(\frac{x+y+z}{2}\)
अब पुनः माना कि नये त्रिभुज की भुजाएँ 2x, 2y तथा 2z हैं एवं s’ इसका अर्द्ध परिमाप है। अतः
s’ = \(\frac{2 x+2 y+2 z}{2}\)
= \(\frac{2(x+y+z)}{2}\) = 2s
∴ s’ = 2s
अब माना कि दोनों त्रिभुजों के क्षेत्रफल क्रमश A तथा A’ हैं तो

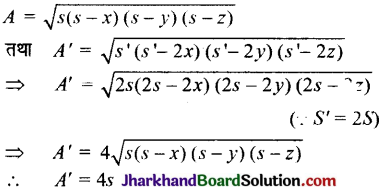
∴ त्रिभुज के क्षेत्रफल में वृद्धि = A’ – A = 4S – S = 3S
प्रतिशत वृद्धि = \(\frac {3S}{S}\) × 100 = 300%
अतः क्षेत्रफल में वृद्धि = 300%