Jharkhand Board JAC Class 9 Maths Important Questions Chapter 14 सांख्यिकी Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 14 सांख्यिकी
बहुविकल्पीय प्रश्न :
प्रश्न 1.
8, 3, 7, 10, 5, 6, 14, 19, 21, 25 का परिसर है :
(A) 22
(B) 17
(C) 25
(D) 14
हल :
परिसर = आँकड़ो की उच्चतम सीमा – उनकी निम्नतम सीमा = 25 – 3 = 22
सही विकल्प (A) है।
![]()
प्रश्न 2.
आँकड़ों के आलेखीय निरूपण में चर प्रदर्शित किए जाते हैं।
(A) X- अक्ष पर
(B) Y-अक्ष पर
(C) क्रमश: दोनों अक्षों पर
(D) मूल बिन्दु पर
हल :
सही विकल्प (B) है।
प्रश्न 3.
किसी वर्ग के अन्तर को कहते हैं :
(A) वर्ग की चौड़ाई
(B) वर्ग की माप
(C) वर्ग-अन्तराल
(D) ये सभी
उत्तर :
सही विकल्प (D) है।
प्रश्न 4.
किसी समस्या के 10 पदों में सबसे अन्तिम पद की संचयी आवृत्ति 60 है। तो N का मान होगा :
(A) 10
(B) 6
(C) 600
(D) 60
हल :
अन्तिम पद की संचयी बारम्बारता = समस्त बारंबारताओं का योग (N) = 60
सही विकल्प (D) है।
![]()
प्रश्न 5.
आँकड़ों में दिए गए 1 – 10, 11 – 20 …….. वर्गों की सतत बनाने के लिए :
(A) निम्न सीमा में से 0.5 घटाएगें
(B) निम्न सीमा में 0.5 जोड़ेंगे
(C) निम्न सीमा में से 0.5 घटाएगें और उच्च सीमा में 0.5 जोड़ेगे,
(D) सतत बन ही नहीं सकता।
हल :
सही विकल्प (C) है।
प्रश्न 6.
आयत चित्र में आयतों की ऊँचाइयाँ उन वर्गों की :
(A) बारम्बारताओं के व्युत्क्रमानुपाती होती हैं.
(B) बारम्बारताओं के समानुपाती होती हैं
(C) वर्ग-अन्तराल के समानुपाती होती हैं।
(D) वर्ग-अन्तराल के व्युत्क्रमानुपाती होती हैं।
हल :
सही विकल्प (B) है।
प्रश्न 7.
असमान वर्ग-अन्तराल की स्थिति में आयत चित्र बनाने के लिए वर्ग की बारम्बारता को पुनः निर्धारित करने का सूत्र है :
पुनः निर्धारित बारम्बारता = ?

हल :
सही विकल्प (A) है।
प्रश्न 8.
वर्ग – चिह्न ज्ञात करने का सूत्र है :
(A) ऊपरी सीमा – निम्न सीमा / 2
(B) (ऊपरी सीमा ÷ निम्न सीमा) × बारम्बारता
(C) ऊपरी सीमा + निम्न सीमा / 2
(D) (ऊपरी सीमा + निम्न सीमा) ÷ बारम्बारता
हल :
सही विकल्प (C) है।
![]()
प्रश्न 9.
चार छात्रों के सांख्यिकी में प्राप्तांक 53, 75, 42, 70 हैं। उनके प्राप्तांकों का समान्तर माध्य है :
(A) 42
(B) 64
(C) 60
(D) 56.
हल :
समान्तर माध्य = प्राप्तांकों का योग / छात्रों की संख्या = \(\frac{53+75+42+70}{4}=\frac{240}{4}\) = 60
सही विकल्प (C) है।
प्रश्न 10.
यदि 5, 7, 9, x का समान्तर माध्य 9 हो, तो x का मान है :
(A) 11
(B) 15
(C) 18
(D) 16
हल :
समान्तर माध्य = आँकड़ों का योग / पदों की संख्या
9 = \(\frac{5+7+9+x}{4}=\frac{21+x}{4}\)
⇒ 9 × 4 = 21 + x
⇒ 36 = 21 + x
∴ x = 36 – 21 = 15
सही विकल्प (B) है।
प्रश्न 11.
बंटन 1, 3, 2, 5, 9 की माध्यिका है :
(A) 3
(B) 4
(C) 2
(D) 20.
हल :
सही विकल्प (A) है।
पदों को आरोही क्रम में रखने पर 1, 2, 3, 5, 9
यहाँ पदों की संख्या (N) = 5 है, जो कि विषम है।
अतः माध्यिका = (\(\frac{N+1}{2}\)) वें पद का मान = (\(\frac{5+1}{2}\)) वें पद का मान = (\(\frac {6}{2}\)) वें पद का मान
= 3 वें पद का मान = 3
![]()
प्रश्न 12.
बंटन 3, 5, 7, 4, 2, 1, 4, 3, 4 का बहुलक है :
(A) 7
(B) 4
(C) 3
(D) 1.
हल :
सही विकल्प (B) है।
ऊपर दी गई सारणी को देखने से स्पष्ट होता है कि 4 की बारम्बारता सबसे अधिक (3 बार) है। अतः इसका बहुलक 4 होगा । अतः सही विकल्प (B) है।
प्रश्न 13.
माध्य के अन्य नाम हैं :
(A) समान्तर माध्य
(B) औसत
(C) मध्यमान
(D) ये सभी
हल :
सही विकल्प (D) है।
प्रश्न 14.
प्रथम 7 विषम संख्याओं का माध्यक होगा :
(A) 7
(B) 8
(C) 9
(D) 5.
हल :
प्रथम 7 विषय संख्याएँ है: 1, 3, 5, 7, 8, 11, 13.
अत : माध्यक = \(\frac{N+1}{2}\) वाँ पद = 7.
सही विकल्प (A) है।
![]()
प्रश्न 15.
प्रथम 11 पूर्ण संख्याओं का माध्य होगा :
(A) 11
(B) 10
(C) 5
(D) 55.
हल :
प्रथम 11 सपूर्ण संख्याएँ हैं 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
अतः \(\bar{x}\) = \(\frac{0+1+2+3+4+5+6+7+8+9+10}{11}\) = \(\frac {55}{11}\) = 5
सही विकल्प (C) है।
लघु एवं दीर्घ प्रश्नोत्तर :
प्रश्न 1.
निम्नलिखित बारम्बारता बंटन का परिसर ज्ञात कीजिए : 2.7, 27, 2.8, 21, 2.4, 3.2, 3.1, 2.8, 3.2.
हल :
बारम्बारता का अधिकतम मान = 3.2
बारम्बारता का न्यूनतम मान = 2.1
∴ परिसर (परास) = अधिकतम मान – न्यूनतम मान = 3.2 – 2.1 = 1.1
प्रश्न 2.
प्राथमिक आँकड़े क्या हैं?
हल :
सांख्यिकीय अन्वेषक जिन आँकड़ों का स्वयं या अपने कार्यकर्ताओं के द्वारा पहली बार संग्रहीत करता है, उन्हें प्राथमिक आँकड़े कहते हैं।
प्रश्न 3.
गौण आँकड़े अर्थात् द्वितीयक आँकड़े क्या हैं?
हल :
वे आँकड़े जिनका पूर्व में अन्य किसी व्यक्ति या संस्था द्वारा संकलन किया जा चुका हो, जो प्रकाशित या अप्रकाशित हो सकते हैं, ऐसे आँकड़ों को द्वितीयक आँकड़े कहते हैं ।
![]()
प्रश्न 4.
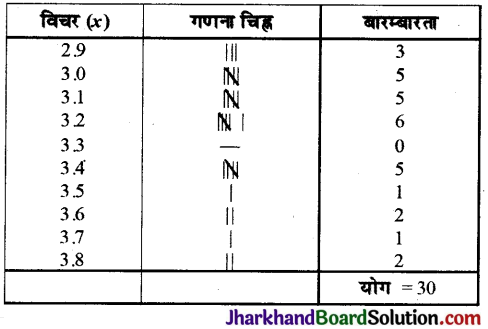
एक गाँव में जन्मे 30 बच्चों का भार (किग्रा में) निम्न प्रकार था :
3.4, 3.6, 3.0, 3.8, 3.6, 3.8, 2.9, 3.4, 2.9, 3.4, 3.0, 3.4, 3.2, 3.1, 3.2, 3.2, 3.1, 3.2, 3.4, 3.0, 3.1, 3.2,3.5, 3.7, 3.1, 3.0, 2.9, 3.0, 3.1, 3.2
उपर्युक्त को बारम्बारता बंटन सारणी में निरूपित कीजिए ।
हल :
बारम्बारता सारणी :
प्रश्न 5.
निम्नलिखित असतत बारम्बारता बंटन सारणी को सतत बारम्बारता बंटन सारणी में बदलिए, जिसमें एक कक्षा के 38 विद्यार्थियों के भार दिये गये हैं और यह भी बताइए कि 35.5 किग्रा तथा 40.5 किग्रा के भार वाले विद्यार्थी किस वर्ग-अन्तराल में रखे जायेंग ?
| भार (किग्रा में) | विद्यार्थियों की संख्या |
| 31-35 36-40 41-45 46-50 51-55 56 60 61-65 66-70 71-75 | 9 5 14 3 1 2 2 1 1 |
| योग | 38 |
हल :
वर्ग 31-35 और 36-40 से
वर्ग 36-40 की निम्न सीमा = 36
वर्ग 31-35 की ऊपरी सीमा = 35
न्यूनतम अन्तर (h) = 36 – 35 = 1
अन्तर का आधा (\(\frac {h}{2}\)) = \(\frac {1}{2}\) = 0.5
इस प्रकार प्रत्येक वर्ग की निम्न सीमा से 0.5 घटा कर और ऊपरी सीमा में 0.5 जोड़कर सतत वर्ग-अन्तराल बनाते हैं।
| भार (किग्रा में) | विद्यार्थियों की संख्या |
| 30.5-35.5 35.5-40.5 40.5-45.5 45.5-50.5 50.5-55.5 55.5-60.5 60.5-65.5 65.5-70.5 70.5-75.5 | 9 5 14 3 1 2 21 1 |
| योग | 38 |
अतः 35.5 किग्रा भार को 35.5 – 40.5 वर्ग – अन्तराल में और 40.5 किग्रा भार को 40.5 – 45.5 वर्ग – अन्तराल में रखते हैं।
![]()
प्रश्न 6.
एक परिवार ने जिसकी मासिक आय ₹ 20,000 है। विभिन्न मदों के अन्तर्गत हर महीने होने वाले खर्च की योजना बनाई थी :
| मद | खर्च |
| ग्रासरी (परचून का समा) किराया बच्चों की शिक्षा दवाइयाँ ईंधन मनोरंजन विविध | 4000 5000 5000 2000 2000 1000 1000 |
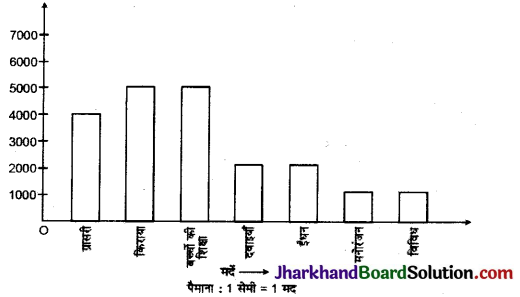
ऊपर दिये गये आँकड़ों का दण्ड आलेख बनाइए ।
हल :
दण्ड आलेख बनाने की विधि :
(i) पहले X- अक्ष और Y – अक्ष खींचते हैं।
(ii) X-अक्ष पर अचर (मद) को निरूपित करते हैं। दो मदों के मध्य समान दूरी रखी जाती है ।
माना पैमानाः 1 सेमी = 1 मद
(iii) Y-अक्ष चर (विभिन्न ) पर खर्च को निरूपित करते हैं। पैमाना : 1 सेमी = ₹ 1,000 ।
(iv) अब दिये गये आँकड़ों के अनुसार तथा दो क्रमागत आयताकार दण्डों के बीच 1 सेमी का खाली स्थान छोड़कर (समान चौड़ाई) आयताकार दण्ड प्रदर्शित करते हैं।
प्रश्न 7.
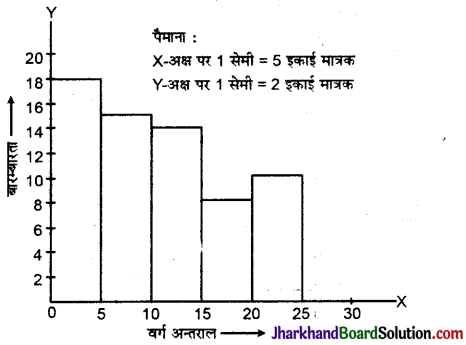
निम्न बारम्बारता सारणी से आयत चित्र बनाइए :

हल :
यहाँ बारम्बारता बंटन वर्गीकृत एवं सतत है। वर्ग अन्तराल भी समान हैं।
(i) X- अक्ष पर पैमाना : 1 सेमी = 5 इकाई मानकर वर्ग-अन्तराल को निरूपित करते हैं जो आयत की चौड़ाई को व्यक्त करता है।
(ii) Y – अक्ष पर पैमानाः 1 सेमी = 2 इकाई मानकर बारम्बारता को अंकित करते हैं जो आयत की ऊँचाई को निरूपित करता है।
![]()
प्रश्न 8.
निम्न बारम्बारता बंटन के लिए बारम्बारता बहुभुज का निर्माण कीजिए :

हल :
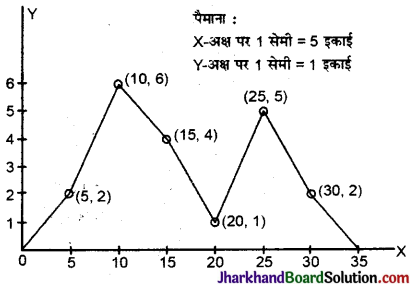
X – अक्ष पर पैमाना (1 सेमी = 5 इकाई) लेकर विचर अंकित किये और Y – अक्ष पर पैमाना (1 सेमी = 2 इकाई) लेकर बारम्बारता अंकित कीं ।
अब बिन्दु (5, 2), (10, 6), (15, 4), (20, 1), (25, 5) और (30, 2) अंकित किये। प्रथम विचर से पहले विचर का मान शून्य आता है। अब बिन्दु (5, 2) को बिन्दु (0, 0) से मिलाया । इसी प्रकार अन्तिम विचर से आगे वाला विचर 35 है। अतः अंतिम बिन्दु (30, 2) को बिन्दु (35, 0) से मिलाया ।
इस प्रकार प्राप्त लेखाचित्र दिए गए बारम्बारता बंटन के लिए बारम्बारता बहुभुज होगा ।
प्रश्न 9.
प्रथम दस विषम संख्याओं का समान्तर माध्य ज्ञात कीजिए ।
हल :
प्रथम दस विषम संख्याएँ क्रमशः 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 हैं।
अतः समान्तर माध्य (\(\bar{x}\)) = \(\frac{1+3+5+7+9+11+13+15+17+19}{10}\) = \(\frac {100}{10}\) = 10
![]()
प्रश्न 10.
एक विद्यालय के सहायक कर्मचारियों का मासिक वेतन (रुपयों में) 1,720, 1,750, 1,760 तथा 1,710 है, तो समान्तर माध्य ज्ञात कीजिए ।
हल :
समान्तर माध्य = कर्मचारियों के मासिक वेतन का योग / कर्मचारियों की संख्या
= \(\frac{1,720+1,750+1,760+1,710}{4}\) = \(\frac {6940}{4}\) = ₹ 1735
अतः समान्तर माध्य = ₹ 1735
प्रश्न 11.
निम्नलिखित बंटन का समान्तर माध्य ज्ञात कीजिए :

हल :
| x | f | fx |
| 0.1 0.2 0.3 0.4 0.5 0.6 | 30 60 20 40 10 50 | 3 12 6 16 5 30 |
| Σf = 210 | Σfx = 72 |
अतः समान्तर माध्य (\(\bar{x}\)) = \(\frac {Σfx}{Σf}\) = \(\frac {72}{210}\)
= 0.342.
प्रश्न 12.
निम्न आँकड़ों की माध्यिका ज्ञात कीजिए : 19, 25, 59, 48, 35, 31, 30, 32, 51.
हल :
दिये गये आँकड़ों को आरोही क्रम में रखने पर,
19, 25, 30, 31, 32, 35, 48, 51, 59
यहाँ कुल पद (n) = 9, जो कि विषम पद है।
अतः माध्यिका = (\(\frac{n+1}{2}\)) वाँ पद = (\(\frac{9+1}{2}\))वाँ पद
= (\(\frac {10}{2}\))वाँ पद = 5वाँ पद = 32
अतः माध्यिका 32।
![]()
प्रश्न 13.
आरोही क्रम में व्यवस्थित चर मान (x) निम्नानुसार हैं : 8 11 12 16 16 + x 20 25 30 यदि माध्यिका 18 हो, तो x का मान ज्ञात कीजिए ।
हल :
यहाँ कुल चरों की संख्या 8 है जो कि समसंख्या है।

⇒ 32 + x = 36 ⇒ x = 36 – 32 = 4
अतः x का मान = 4.
प्रश्न 14.
एक कक्षा के 20 छात्रों की आयु (वर्षों में) निम्न प्रकार है :
15 16 13 14 14 13 15 14 13 13 14 12 15 14 16 13 14 14 13 15
इन्हें बारम्बारता बंटन सारणी में व्यक्त कर बहुलक ज्ञात कीजिए ।
हल :
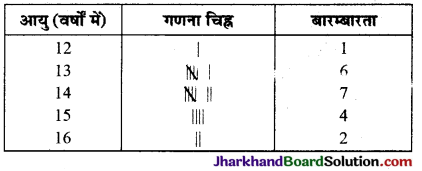
सारणी से स्पष्ट है कि सबसे अधिक बारम्बारता 7, आयु 14 वर्ष की है।
अतः बहुलक 14 है।
प्रश्न 15.
कुछ विद्यार्थियों के प्राप्तांक नीचे दिये हुए हैं, प्राप्तांकों का बहुलक ज्ञात कीजिए :

हल :
सारणी से स्पष्ट है कि 40 अंक प्राप्त करने वाले विद्यार्थियों की संख्या सर्वाधिक 26 है
अत: बहुलक 40 है।
![]()
प्रश्न 16.
क्रिकेट के एक खिलाड़ी ने 10 पारियों में क्रमश: 60, 62, 56, 64, 0, 57, 33, 27, 9 और 71 रन बनाये । उनके इन पारियों के रनों का औसत ज्ञात कीजिए।
हल :

प्रश्न 17.
यदि 3, 4, 8, 5, x, 3, 2, 1 अंकों का समान्तर माध्य 4 हो, तो x का मान ज्ञात कीजिए ।
हल :
समान्तर माध्य (\(\bar{x}\)) = पदों का योग / पदों की संख्या
4 = \(\frac{3+4+8+5+x+3+2+1}{8}\)
⇒ 4 × 8 = 26 + x
⇒ 32 = 26 + x
∴ x = 32 – 26 = 6
अत: x = 6.
प्रश्न 18.
यदि 6, 9, 5, 8, x, 4 अंकों का समान्तर माध्य 7 हो, तो x का मान ज्ञात कीजिए ।
हल :
चूँकि समान्तर माध्य (\(\bar{x}\)) = \(\frac{\Sigma x_i}{N}\)
\(\bar{x}\) = \(\frac{6+9+5+8+x+4}{6}\)
⇒ \(\bar{x}\) = \(\frac{32+x}{6}\) = 7 (∵ \(\bar{x}\) = 7)
⇒ 32 + x = 42
⇒ x = 42 – 32
∴ x = 10
![]()
प्रश्न 19.
किसी बारम्बारता बंटन का समान्तर माध्य 18.50 है तथा Σf = 20, तो Σfx का मान ज्ञात कीजिए ।
हल :
हम जानते है कि,
\(\bar{x}\) = \(\frac {Σfx}{Σf}\)
⇒ समान्तर माध्य, 18.50 = \(\frac {Σfx}{20}\)
⇒ Σfx = 18.50 × 20
∴ Σfx = 370
प्रश्न 20.
किसी फुटबाल खिलाड़ी ने कुछ मैचों में 3 गोल प्रति मैच की औसत से 39 गोल किए। खिलाड़ी द्वारा खेले गए मैचों की संख्या बताइए।
हल :
औसत \(\bar{x}\) = 8 तथा कुल गोल Σx = 39.
∴ \(\bar{x}\) = \(\frac {Σfx}{N}\)
⇒ 3 = \(\frac {39}{N}\)
⇒ 3 × N = 39
⇒ N = \(\frac {39}{N}\) = 13