JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.1

प्रश्न 1.
दो घनों, जिनमें से प्रत्येक का आयतन 64 सेमी³ है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :

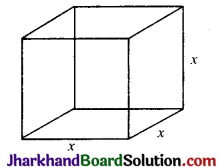
माना कि घन की प्रत्येक भुजा = x सेमी
घन का आयतन = 64 सेमी³ (दिया है)
हम जानते हैं,
घन का आयतन = (भुजा)³
⇒ 64 = (x)³
⇒ x = \(\sqrt[3]{64}\)
∴ x = 4 सेमी
∴ घन की भुजा = 4 सेमी
∵ जब दोनों घनों को साथ-साथ जोड़ा जाता है, तो घनाभ बन जाता है।
जिसकी लम्बाई (l) = 2x = 2 × 4 = 8 सेमी
चौड़ाई (b) = x = 4 सेमी
ऊँचाई (h) = x = 4 सेमी

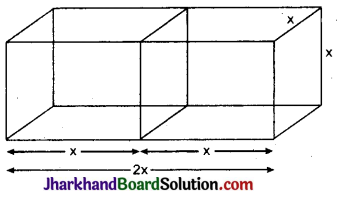
∴ घनाभ का पृष्ठीय क्षेत्रफल = 2 × (lb + bh + hl)
= 2 × (8 × 4 + 4 × 4 + 4 × 8)
= 2 × (32 + 16 + 32)
= 2 × 80
= 160 वर्ग सेमी
अतः नये घनाभ का पृष्ठीय क्षेत्रफल
= 160 वर्ग सेमी

प्रश्न 2.
कोई बर्तन एक खोखले अर्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन ध्यारोपित है। अर्द्धगोले का व्यास 14 सेमी है और इस बर्तन (पात्र) की कुल चाई 13 सेमी है। इस बर्तन का आन्तरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

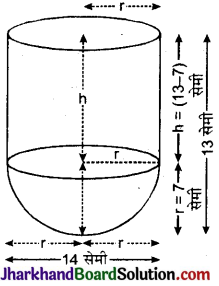
हल :
दिया है,
अर्द्धगोले तथा बेलन की उभयनिष्ठ त्रिज्या (r) = \(\frac {14}{2}\) = 7 सेमी
∴ अर्द्धगोले की त्रिज्या (r) = 7 सेमी
बेलन की त्रिज्या (r) = 7 सेमी
∵ बर्तन की कुल ऊँचाई = 13 सेमी
∴ बेलन की ऊँचाई (h) = (13 – 7) = 6 सेमी
बर्तन का आन्तरिक पृष्ठीय क्षेत्रफल
= बेलन का आन्तरिक पृष्ठीय क्षेत्रफल + अर्द्धगोले का आन्तरिक पृष्ठीय क्षेत्रफल
= 2πrh + 2πr² = 2πr (h + r)
= 2 × \(\frac {22}{7}\) × 7× (6 + 7)
= 44 × 13 = 572 वर्ग सेमी
अतः बर्तन (पात्र) का कुल आन्तरिक पृष्ठीय क्षेत्रफल = 572 वर्ग सेमी।

प्रश्न 3.
एक खिलौना त्रिज्या 3.5 सेमी वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की सम्पूर्ण ऊंचाई 15.5 सेमी है। इस खिलौने का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

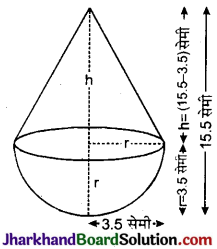
हल :
दिया है,
शंकु की त्रिज्या (r) = अर्द्धगोले की त्रिज्या (r)
= 3.5 सेमी
तथा खिलौने की ऊँचाई = 15.5 सेमी
∴ शंकु की ऊँचाई (h) = (15.5 – 3.5) सेमी = 12 सेमी
शंकु की तिर्यक ऊँचाई (l) = \(\sqrt{(3 \cdot 5)^2+(12)^2}\)
= \(\sqrt{(3 \cdot 5)^2+(12)^2}\)
= \(\sqrt{(3 \cdot 5)^2+(12)^2}\)
= \(\sqrt{12 \cdot 25+144}\)
= \(\sqrt{156.25}\)
∴ l = 12.5 सेमी
बर्तन का कुल पृष्ठीय क्षेत्रफल = शंकु का पृष्ठीय क्षेत्रफल + अर्द्धगोले का पृष्ठीय क्षेत्रफल
= πrl + 2πr²
= πr (l + 2r)
= \(\frac {22}{7}\) × 3.5 × (12.5 + 2 × 3.5)
= 22 × 0.5 × (12.5 + 7)
= 11 × 19.5
= 214.5 सेमी²
अतः बर्तन का कुल पृष्ठीय क्षेत्रफल
= 214.5 वर्ग सेमी

प्रश्न 4.
भुजा 7 सेमी वाले एक घनाकार ब्लॉक के ऊपर एक अर्द्धगोला रखा हुआ है। अर्द्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल
दिया है,
∵ अर्द्धगोले का आधार घन के ऊपरी फलक पर टिका है ।

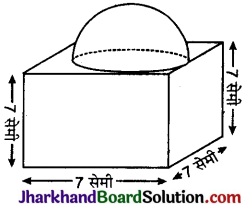
∴ अर्द्धगोले का अधिकतम व्यास = घन की भुजा 7 सेमी (दिया है)
∴ अर्द्धगोले की त्रिज्या (r) = \(\frac {7}{2}\)सेमी
ठोस का पृष्ठीय क्षेत्रफल
= घन का सम्पूर्ण पृष्ठीय क्षेत्रफल + अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल – वृत्तीय आधार का क्षेत्रफल
= 6 × (भुजा)² + 2πr² – πr²
= 6 × (भुजा)² + πr²
= 6 × (7)² + \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\)
= 6 × 49 + \(\frac {77}{2}\)
= 294 + 38.5 = 332.5 वर्ग सेमी
अतः अर्द्धगोले का अधिकतम व्यास = 7 सेमी
तथा ठोस का पृष्ठीय क्षेत्रफल = 332.5 वर्ग सेमी।

प्रश्न 5.
एक घनाकार ब्लॉक के एक फलक को अन्दर की ओर से काटकर एक अर्द्धगोलाकार गड्डा इस प्रकार बनाया गया है कि अर्द्धगोले का व्यास घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
माना कि घन की भुजा = a

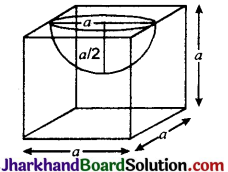
∴ अर्द्धगोले का व्यास = घन की भुजा
⇒ 2r = a
⇒ r = \(\frac {a}{2}\)
अर्द्धगोले की त्रिज्या (r) = \(\frac {a}{2}\)
शेष बचे ठोस का पृष्ठीय क्षेत्रफल = घन का कुल पृष्ठीय क्षेत्रफल – घन के तल का क्षेत्रफल + अर्द्धगोले का आन्तरिक वक्र पृष्ठीय क्षेत्रफल
= 6a² – πr² + 2πr²
= 6a² + πr²
= 6a² + π(\(\frac {a}{2}\))²
= 6a² + π\(\frac{a^2}{4}\)
= a²[6 + \(\frac {π}{4}\)]सेमी²
= \(\frac{a^2}{4}\)(24 + π)सेमी²
अतः शेष बचे ठोस का पृष्ठीय क्षेत्रफल
= \(\frac{a^2}{4}\)(24 + π) वर्ग सेमी

प्रश्न 6.
दवा का एक कैप्सूल (capsule) एक बेलन के आकार का है जिसके दोनों सिरों पर एक-एक अर्द्धगोला लगा हुआ है (देखिए आकृति)। पूरे कैप्सूल की लम्बाई 14 मिमी है और उसका व्यास 5 मिमी है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल :
दिया है,
कैप्सूल का व्यास = 5 मिमी
∴ बेलनाकार भाग तथा अर्ध गोले की उभयनिष्ठ त्रिज्या(r) = \(\frac {5}{2}\) मिमी

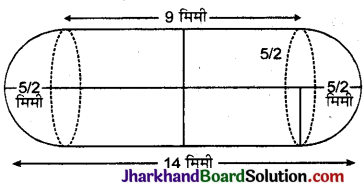
कैप्सूल की आन्तरिक लम्बाई (h) = 14 मिमी
बेलनाकार भाग की लम्बाई = [14 – \(\frac {5}{2}\) – \(\frac {5}{2}\)] मिमी
= (14 – 5) मिमी = 9 मिमी
कैप्सूल का पृष्ठीय क्षेत्रफल = बेलन का पृष्ठीय क्षेत्रफल + 2 अर्द्धगोलों का पृष्ठीय क्षेत्रफल
= 2πrh + 2 × (2πr²)
= 2πrh + 4πr² = 2πr (h + 2r)
= 2 × \(\frac{22}{7} \times \frac{5}{2}\) × (9 + 2 × \(\frac {5}{2}\))
= \(\frac {110}{7}\) × (9 + 5) = \(\frac{110 \times 14}{7}\) = 220 मिमी²
अतः कैप्सूल का पृष्ठीय क्षेत्रफल = 220 वर्ग मिमी

प्रश्न 7.
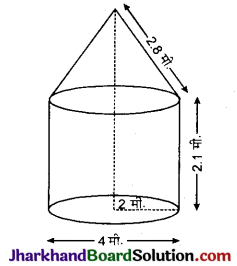
कोई तम्बू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमशः 2.1 मीटर और 4 मीटर हैं तथा शंकु की तिर्यक ऊँचाई 2.8 मीटर है तो इस तम्बू को बनाने में प्रयुक्त कैनवास (canvas) का क्षेत्रफल ज्ञात कीजिए। साथ ही, ₹500 प्रति वर्ग मीटर की दर से इसमें प्रयुक्त कैनवास की लागत ज्ञात कीजिए। (ध्यान दीजिए कि तम्बू के आधार को कैनवास से नहीं ढका जाता है।)

हल :
दिया है,
बेलन का व्यास = शंकु का व्यास = 4 मी.
∴ बेलन और शंकु की उभयनिष्ठ त्रिज्या (r) = \(\frac {4}{2}\)
= 2 मीटर
शंकु की त्रिज्या = बेलन की त्रिज्या = r = 2सेमी
बेलन की ऊँचाई (h) = 2.1 मीटर
तथा शंकु की तिर्यक ऊँचाई (l) = 2.8 मीटर
तम्बू का वक्र पृष्ठीय क्षेत्रफल = बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल + शंक्वाकार भाग का वक्र पृष्ठीय क्षेत्रफल
= 2πrh + πrl = πr (2h + l)
= \(\frac {22}{7}\) × 2 × (2 × 2.1 + 2.8)
= \(\frac {22}{7}\) × (4.2 + 2.8)
= \(\frac {22}{7}\) × 7 = 44 मीटर²
∴ तम्बू का वक्र पृष्ठीय क्षेत्रफल = 44 मीटर²
∵ 1 मीटर² कैनवास की लागत = ₹ 500
∴ 44 मीटर² कैनवास की लागत = 44 × 500 = ₹ 22000
अतः कैनवास की कुल लागत = ₹ 22000

प्रश्न 8.
ऊँचाई 2.4 सेमी और व्यास 1.4 सेमी वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल (cavity) काट लिया जाता है। शेष बचे ठोस का निकटतम वर्ग सेण्टीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
दिया है,
बेलन का व्यास = 1.4 सेमी
∴ बेलन तथा शंकु की उभयनिष्ठ त्रिज्या (r) = \(\frac {1.4}{2}\) = 0.7 सेमी

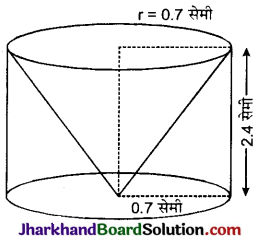
बेलन की ऊँचाई (h) = 2.4 सेमी
शंक्वाकार खोल की तिर्यक ऊँचाई (l) = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(0 \cdot 7)^2+(2 \cdot 4)^2}\)
= \(\sqrt{0.49+5 \cdot 76}\)
= \(\sqrt{6.25}\)
l = 2.5 सेमी
शेष बचे ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + बेलन के आधार का क्षेत्रफल + शंक्वाकार का वक्र पृष्ठीय क्षेत्रफल
= 2πrh + πr² + πrl = πr(2h + r + l)
= \(\frac {22}{7}\) × 0.7 × [2 × 2.4 + 0.7 + 2.5]
= 2.2 × [4.8 + 0.7 + 2.5]
= 2.2 × 8 = 17.6 ≈ 8 वर्ग सेमी
अतः शेष बचे ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = 18 वर्ग सेमी

प्रश्न 9.
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्द्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसा कि आकृति में दर्शाया गया है। यदि बेलन की ऊँचाई 10 सेमी है और आधार की त्रिज्या 3.5 सेमी है, तो इस वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

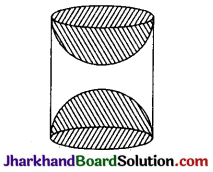
हल :
दिया है,
बेलन की त्रिज्या (r) = 3.5 सेमी
अर्द्धगोले की त्रिज्या (r) = 3.5 सेमी
तथा बेलन की ऊँचाई (h) = 10 सेमी
वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + दोनों अर्द्धगोलों का पृष्ठीय क्षेत्रफल
= 2πrh + 2 × 2πr²
= 2πrh + 4πr² = 2πr (h + 2r)
= 2 × \(\frac {22}{7}\) × 3.5 × (10 + 2 × 3.5)
= 2 × 22 × 0.5 × (10 + 7)
= 22 × 17 = 374 वर्ग सेमी
अतः वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल = 374 वर्ग सेमी