Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.5 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 6 त्रिभुज Exercise 6.5
प्रश्न 1.
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लम्बाई भी लिखिए:
(i) 7 सेमी, 24 सेमी 25 सेमी
(ii) 3 सेमी, 8 सेमी, 6 सेमी
(iii) 50 सेमी, 80 सेमी, 100 सेमी
(iv) 13 सेमी, 12 सेमी, 5 सेमी
हल:
(i) माना कि ΔABC में,
AB = 7 सेमी
BC = 24 सेमी
और AC = 25 सेमी
अब AB2 + BC2 = (7)2 + (24)2
= 49 + 576
= 625
तथा AC2 = (25)2 = 625
∴ AB2 + BC2 = AC2
अत: पाइथागोरस प्रमेय के विलोम से ΔABC समकोण त्रिभुज है जिसमें ∠B समकोण है तथा कर्ण की लम्बाई = 25 सेमी।
(ii) माना कि ΔABC में,
AB = 3 सेमी
BC = 6 सेमी
और AC = 8 सेमी
AB2 + BC2 = (3)2 + (6)2
= 9 + 36 = 45
जबकि AC2 = (8)2 = 64
∵ AB2 + BC2 ≠ AC2
अत: ΔABC समकोण Δ नहीं है।
(iii) माना कि ΔMNP में
MN = 50 सेमी
NP = 80 सेमी
और MP = 100 सेमी
MN2 + NP2 = (50)2 + (80)2
= 2500 + 6400 = 8900
जबकि MP2 = (100)2 = 10000
अत: MN2 + NP2 ≠ MP2
अत: ΔMNP समकोण त्रिभुज नहीं है।
(iv) माना कि ΔPQR में,
PQ = 13 सेमी
QR = 12 सेमी
PR = 5 सेमी
(PR)2 + (QR)2 = (5)2 + (12)2 = 25 + 144
= 169
PQ2 = (13)2 = 169
∵ PR2 + QR2 = PQ2
अत: पाइथागोरस प्रमेय के विलोम से, ΔPQR एक समकोण त्रिभुज है जिसमें ∠R समकोण है और कर्ण की लम्बाई = 13 सेमी।
![]()
प्रश्न 2.
PQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिन्दु M इस प्रकार स्थित है कि PM ⊥ QR है। दर्शाइए कि PM2 = QM.MR है।
हल:
दिया है: समकोण ΔPQR में कोण P समकोण है तथा PM ⊥ QR है।
सिद्ध करना है: PM2 = QM.MR
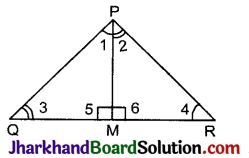
उपपत्ति: ∵ ΔPQR एक समकोण त्रिभुज है तथा PM कर्ण QR पर लम्ब है।
अतः प्रमेय 6.7 के अनुसार,
ΔQPM ~ ΔPRM
⇒ \(\frac{P M}{R M}=\frac{Q M}{P M}\)
(∵ समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं।)
PM2 = RM × QM.
प्रश्न 3.
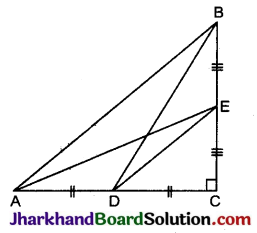
आकृति में, ABD एक समकोण त्रिभुज है जिसका कोण समकोण है तथा AC ⊥ BD है। दर्शाइए कि:
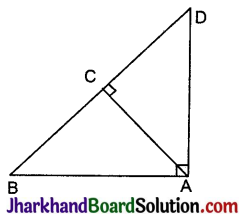
(i) AB2 = BC.BD
(ii) AC2 = BC.DC
(iii) AD2 = BD.CD
हल:
दिया है: ABD एक समकोण त्रिभुज है जिसमें ∠A समकोण है तथा AC ⊥ BD है।
सिद्ध करना है:
(i) AB2 = BC.BD
(ii) AC2 = BC.DC
(iii) AD2 = BD.CD
उपपत्ति: (i) ∵ ΔABD एक समकोण त्रिभुज है तथा AC कर्ण BD पर लम्ब है।
अतः प्रमेय 6.7 के अनुसार,
ΔDAB ~ ΔACB
⇒ \(\frac{A B}{C B}=\frac{B D}{A B}\)
⇒ AB2 = BC × BD
(ii) प्रमेय 6.7 के अनुसार,
ΔDCA ~ ΔACB
⇒ \(\frac{D C}{A C}=\frac{A C}{B C}\)
[दो समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं]
⇒ AC2 = BC × DC
(iii) प्रमेय 6.7 के अनुसार,
ΔDAB ~ ΔDCA
⇒ \(\frac{D A}{D C}=\frac{D B}{A D}\)
AD2 = DB × DC
![]()
प्रश्न 4.
ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है। सिद्ध कीजिए कि AB2 = 2AC2 है।
हल:
दिया है: ΔABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है।
सिद्ध करना है: AB2 = 2AC2
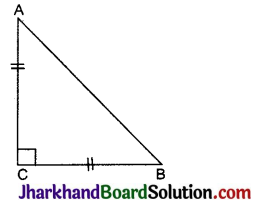
उपपत्ति: ΔACB में,
∠C = 90°
∴ पाइथागोरस प्रमेय से,
AB2 = AC2 + BC2
= AC2 + AC2 (∵ AC = BC)
∴ AB2 = 2AC2
प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है। यदि AB2 = 2AC2 है, तो सिद्ध कीजिए कि ACB एक समकोण त्रिभुज है।
हल:
दिया है: ΔABC समद्विबाहु त्रिभुज है जिसमें AC = BC तथा AB2 = 2AC2 है।
सिद्ध करना है: ΔABC एक समकोण त्रिभुज है।
उपपत्ति: AB2 = 2AC2 (दिया है)
AB2 = AC2 + AC2
AB2 = AC2 + BC2 (∵ AC = BC)
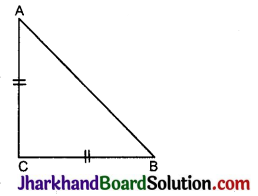
∴ पाइथागोरस प्रमेय के विलोम से,
ΔACB एक समकोण त्रिभुज है।
प्रश्न 6.
एक समबाहु त्रिभुज ABC की प्रत्येक भुजा 2a है। उसके प्रत्येक शीर्षलम्ब की लम्बाई ज्ञात कीजिए।
हल:
ΔABC एक समबाहु त्रिभुज है जिसकी प्रत्येक भुजा 2a है।
AB = AC = BC = 2a
AD ⊥ BC
BD = CD = \(\frac{2a}{2}\) = a
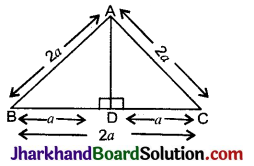
अब समकोण ΔADB में,
AB2 = AD2 + BD2
(2a)2 = (AD)2 + (a)2
4a2 = (AD)22 + a2
(AD)2 = 4a2 – a
(AD)2 = 3a2
AD = \(\sqrt{3}\)a या a\(\sqrt{3}\)
अतः शीर्ष लम्ब की लम्बाई = a\(\sqrt{3}\)
![]()
प्रश्न 7.
सिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है।
हल:
दिया है: समचतुर्भुज ABCD के विकर्ण AC और BD बिन्दु O पर प्रतिच्छेद करते हैं।
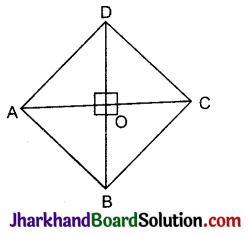
सिद्ध करना है:
AB2 + BC2 + CD2 + DA2 = AC2 + BD2
उपपत्ति: हम जानते हैं कि समचतुर्भुज के विकर्ण समकोण पर समद्विभाजित करते हैं। अतः समकोण ΔAOB में,
OA2 + OB2 = AB2 …(1)
इसी प्रकर ΔBOC, ΔCOD और ΔAOD में क्रमश:
OB2 + OC2 = BC2 …(2)
OC2 + OD2 = CD22 …(3)
और OA2 + OD2 = AD2 …(4)
अत: समीकरण (1), (2) (3) और (4) को जोड़ने पर,
AB2 + BC2 + CD2 + AD2 = 2(OA2 + OC2 + OB2 + OD2)
यहाँ OA = OC = \(\frac{A C}{2}\) और OB = OD = \(\frac{B D}{2}\)
अत: AB2 + BC2 + CD2 + AD2 = \(2\left[\frac{A C^2}{4}+\frac{A C^2}{4}+\frac{B D^2}{4}+\frac{B D^2}{4}\right]\)
⇒ AB2 + BC2 + CD2 + AD2 = AC2 + BD2
प्रश्न 8.
आकृति में, ΔABC के अभ्यन्तर में स्थित कोई बिन्दु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि:
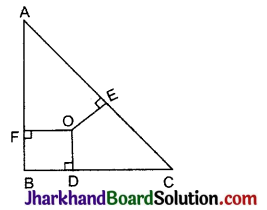
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
हल:
दिया है: ΔABC के अन्दर एक बिन्दु O है जिससे भुजाओं BC, CA तथा AD पर क्रमश: OD, OE, और OF लम्ब खींचे गए हैं।
सिद्ध करना है:
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
रचना : रेखाखण्ड OA, OB तथा OC को मिलाया।
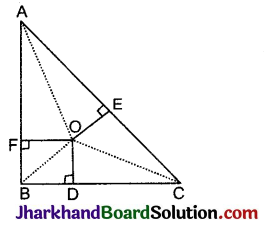
उपपत्ति: (i) समकोण ΔAFO में,
AF2 + OF2 = OA2 …(1)
समकोण ΔODB में,
BD2 + OD2 = OB2 …(2)
समकोण ΔOEC में,
CE2 + OE2 = OC2 …(3)
समीकरण (1), (2) व (3) को जोड़ने पर,
AF2 + BD2 + CE2 + OF2 + OD2 + OE2 = OA2 + OB2 + OC2
⇒ AF2 + BD2 + CE2 = OA2 + OB2 + OC2 – OD2 – OE2 – OF2
⇒ OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
(ii) समकोण ΔODB में,
OD2 + BD2 = OB2 …(4)
समकोण ΔODC मैं,
OD2 + CD2 = OC2 …(5)
समीकरण (4) में से (5) को घटाने पर,
BD2 – CD2 = OB2 – OC2 …(6)
इसी प्रकार समकोण ΔOEC तथा ΔOEA में,
CE2 – AE2 = OC2 – OA2 …(7)
और समकोण ΔOFA तथा ΔOFB में,
AF2 – BF2 = OA2 – OB2 …(8)
समीकरण (6), (7) व (8) को जोड़ने पर,
BD2 + CE2 + AF2 – CD2 – AE2 – BF2 = 0
⇒ AF2 + BD2 + CE2 = AE2 + CD2 + BF2
द्वितीय विधि: समीकरण (1) से
पुन: AF2 + BD2 + CE2 = (OA2 – OE2) + (OC2 – OD2) + (OB2 – OF2)
= AE2 + CD2 + BF2
{∵ AE2 = AO2 – OE2
CD2 = OC2 – OD2
BF2 = OB2 – OF2}
![]()
प्रश्न 9.
10 मी. लम्बी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8 मी. की ऊंचाई पर स्थित एक खिड़की तक पहुँचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।
हल:
माना खिड़की की धरती से ऊँचाई (AB) = 8 मीटर
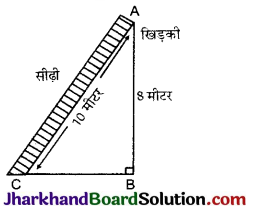
तथा AC एक सीढ़ी है।
सीढ़ी की लम्बाई (AC) = 10 मीटर
सीढ़ी के निचले सिरे और दीवार के आधार के बीच की दूरी (BC) = ?
समकोण ΔABC में,
AC2 = AB2 +BC2 ( पाइथागोरस प्रमेय से )
(10)2 = (8)2 + BC2
⇒ BC2 = 102 – 82 = 100 – 64 = 36
BC = 6 मीटर
अतः सीढ़ी के निचले सिरे और दीवार के आधार के बीच की दूरी = 6 मीटर।
प्रश्न 10.
18 मीटर ऊँचे एक ऊर्ध्वाधर खम्भे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूंटे से जुड़ा हुआ है। खम्भे के आधार से खूंटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे, जबकि तार की लम्बाई 24 मीटर है।
हल:
माना खम्भे की ऊँचाई (AB) = 18 मीटर
तथा तार की लम्बाई (AC) = 24 मीटर
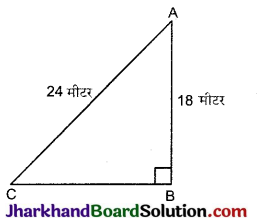
माना खूँटे की स्थिति C है। इसकी खम्भे के आधार से दूरी (BC) = ?
समकोण ΔABC में,
AC2 = AB2 + BC2 (पाइथागोरस प्रमेय से)
(24)2 = (18)2 + (BC)2
⇒ (BC)2 = (24)2 – (18)2
⇒ (BC)2 = 576 – 324
⇒ BC = \(\sqrt{252}\)
∴ BC = 6\(\sqrt{7}\) मीटर
अतः खम्भे के आधार से खूँट की दूरी = 6\(\sqrt{7}\) मीटर या 15.87 मीटर।
![]()
प्रश्न 11.
एक हवाई जहाज एक हवाई अड्डे से उत्तर की ओर 1000 किमी / घण्टा की चाल से उड़ता है। इसी समय एक अन्य हवाई जहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 किमी/घण्टा की चाल से उड़ता है। 1\(\frac{1}{2}\) घण्टे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी ?
हल:
माना कि O बिन्दु हवाई अड्डे को दर्शाता है।
पहले हवाई जहाज की चाल = 1000 किमी / घण्टा
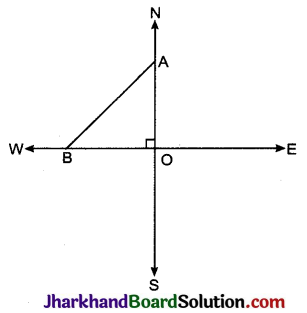
पहले हवाई जहाज द्वारा O बिन्दु से उत्तर की और 1\(\frac{1}{2}\) घण्टे में तय की गई दूरी,
OA = 1000 × 1\(\frac{1}{2}\)
[∵ दूरी चाल × समय]
∴ OA = 1000 × \(\frac{3}{2}\) = 1500 किमी
दूसरे हवाई जहाज की चाल = 1200 किमी / घण्टा
दूसरे हवाई जहाज द्वारा बिन्दु O से पश्चिम की ओर 1\(\frac{1}{2}\) घण्टे में तय की गई दूरी,
OB = 1200 × 1\(\frac{1}{2}\)
∴ OB = 1200 × \(\frac{3}{2}\) = 1800 किमी
समकोण ΔAOB में, पाइथागोरस प्रमेय से,
AB2 = OA2 + OB2
= (1500)2 + (1800)2
= 2250000 + 3240000
= 5490000
∴ AB = \(\sqrt{5490000}\)
= 300\(\sqrt{61}\)
अतः दोनों हवाई जहाजों के बीच की दूरी (AB) = 300\(\sqrt{61}\) किमी।
प्रश्न 12.
दो खम्भे जिनकी ऊँचाइयाँ 6 मीटर और 11 मीटर हैं, समतल भूमि पर खड़े हैं। यदि इनके निचले सिरों के बीच की दूरी 12 मी है, तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
हल:
माना कि एक खम्भे की ऊँचाई (AB) = 11 मीटर
तथा दूसरे खम्भे की ऊँचाई (CD) = 6 मीटर
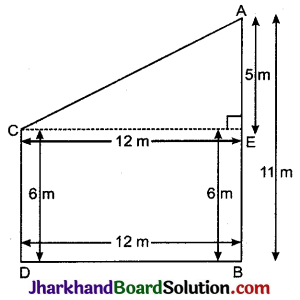
खम्भों के आधारों के बीच की दूरी (BD) = 12 मीटर C से AB पर CE लम्ब खींचते हैं अर्थात् CE ⊥ AB
BE = DC = 6 मीटर
AE = AB – BE = 11 – 6
∴ AE = 5 मीटर
तथा CE = BD = 12 मीटर
समकोण ΔAEC में,
AC2 = AE2 + CE2
AC2 = (5)2 + (12)2
= 25 + 144 = 169
AC = \(\sqrt{169}\)
∴ AC = 13 मीटर
अतः खम्भों के ऊपरी सिरों के बीच की दूरी = 13 मीटर
![]()
प्रश्न 13.
एक त्रिभुज ABC जिसका कोण C समकोण है, की भुजाओं CA और CB पर क्रमश: बिन्दु D और E स्थित हैं। सिद्ध कीजिए कि AE2 + BD2 = AB2 + DE2
हल:
दिया है: ΔABC एक समकोण त्रिभुज है जिसमें ∠C समकोण है तथा भुजाओं CA और CB पर क्रमश: बिन्दु D और E स्थित हैं।
सिद्ध करना है: AE2 + BD2 = AB2 + DE2
उपपत्ति: समकोण ΔBCA में,
पाइथागोरस प्रमेय से,
AB2 = BC2 + CA2 …(1)
समकोण ΔECD में,
DE2 = EC2 + DC2 …(2)
(पाइथागोरस प्रमेय से)
समकोण ΔACE में,
AE2 = AC2 + CE2 …(3)
समकोण ΔBCD में,
BD2 = BC2 + CD2 …(4)
समीकरण (3) व (4) को जोड़ने पर,
AE2 + BD2 = AC2 + CE2 + BC2 + CD2
= (AC2 + BC2) + (CE2 + CD2)
= AB2 + DE2 [समीकरण (1) व (2) से]
अतः AE2 + BD2 = AB2 + DE2
प्रश्न 14.
किसी ΔABC के शीर्ष A से भुजा BC पर डाला गया लम्ब BC को बिन्दु D पर इस प्रकार प्रतिच्छेदित करता है कि DB = 3 CD है। सिद्ध कीजिए कि 2AB2 = 2AC2 + BC2 है।
हल:
दिया है: ΔABC में आधार BC पर शीर्ष A से AD लम्ब इस प्रकार डाला गया है कि BD = 3CD
सिद्ध करना है: 2AB2 = 2AC2 + BC2
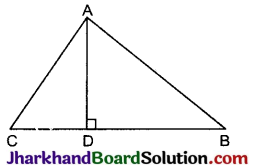
उपपत्ति: समकोण ΔADC में,
AC2 = AD2 + CD2 …(i)
समकोण ΔADB में,
AB2 = AD2 + BD2
दोनों ओर 2 से गुणा करने पर,
2AB2 = 2AD2 + 2BD2
2AB2 = 2(AC2 – CD2) + 2(3CD)2
[∵AD2 = AC2 – CD2; BD = 3CD]
⇒ 2AB2 = 2AC2 – 2CD2 + 18 CD2
= 2AC2 + 16CD2
= 2AC2 + (4CD)2
= 2AC2 + (CD + 3CD)
= 2AC2 + (CD + BD)2 (∵ 3CD = BD)
= 2AC2 + BC2 (∵BC = CD + BD)
अत : 2AB2 = 2AC2 + BC2
प्रश्न 15.
किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि BD = \(\frac{1}{3}\)BC है। सिद्ध कीजिए कि 9AD = 7AB2 है।
हल:
दिया है: ΔABC एक समबाहु त्रिभुज है जिसके आधार BC पर एक बिन्दु D इस प्रकार है कि
BD = \(\frac{1}{3}\)BC
सिद्ध करना है: 9AD2 = 7AB2
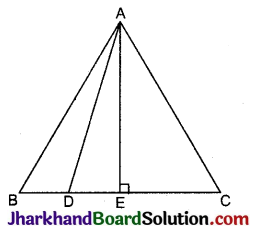
रचना : A से BC पर AE लम्ब खींचा अर्थात् AE ⊥ BC है।
उपपत्ति: समबाहु त्रिभुज ABC में,
AE ⊥ BC
BE = CE = \(\frac{1}{2}\)BC
BE = \(\frac{1}{2}\)AB …(1)
(∵ AB = BC)
समकोण त्रिभुज AEB में,
AB2 = BE2 + AE2
⇒ AB2 = \(\left(\frac{1}{2} A B\right)^2\) + AE2
⇒ AB2 = \(\frac{1}{2}\)AB2 + AE2
AB2 – \(\frac{1}{4}\)AB2 = AE2
\(\frac{3}{4}\)AB2 = AE2 …(2)
समकोण त्रिभुज AED में,
AE2 + DE2 = AD2
⇒ AE2 = AD2 – DE2 …(3)
BD = \(\frac{1}{3}\)BC (दिया है)
⇒ BD = \(\frac{1}{3}\)AB …(4)
समीकरण (1) में से (4) को घटाने पर,
⇒ BE – BD = \(\frac{1}{2}\)AB – \(\frac{1}{3}\)AB
⇒ DE = \(\frac{1}{6}\)AB …(5)
समीकरण (2) तथा (3) से,
\(\frac{3}{4}\)AB2 = AD2 – DE2
⇒ \(\frac{3}{4}\)AB2 = AD2 – (\(\frac{1}{6}\)AB)2
⇒ \(\frac{3}{4}\)AB2 = AD2 – \(\frac{1}{36}\)AB2
⇒ \(\frac{3}{4}\)AB2 + \(\frac{1}{36}\)AB2 = AD2
⇒ \(\frac{27 A B^2+A B^2}{36}\) = AD2
⇒ 28AB2 = 36AD2
⇒ 7AB2 = 9AD2
अतः 9AD2 = 7AB2
![]()
प्रश्न 16.
किसी समबाहु त्रिभुज में सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलम्ब के वर्ग के चार गुने के बराबर होता है।
हल:
दिया है: ΔABC एक समबाहु त्रिभुज है जिसमें AB = BC = CA तथा AD ⊥ DC है।
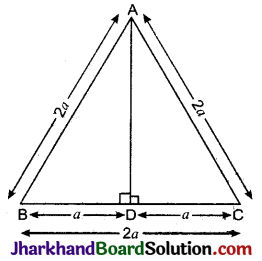
सिद्ध करना है: 3AB2 = 4AD2
उपपत्ति: ΔABC में,
माना कि AB = BC = CA = 2a
∵ AD ⊥ BC
∴ BD = DC = \(\frac{1}{2}\)BC = \(\frac{1}{2}\) × 2a = a
समकोण ΔABD में,
AB2 = AD2 + BD2
(2a)2 = AD2 + (a)2
⇒ (AD)2 = 4a2 – a2
⇒ AD2 = 3a2
[∵ AB = 2a
a = \(\frac{AB}{2}\)]
⇒ AD2 = 3 × \(\left[\frac{A B}{2}\right]^2\)
⇒ AD2 = \(\frac{3 A B^2}{4}\)
∴ AD2 = 3AB2
अर्थात् 3AB2 = 4AD2
![]()
प्रश्न 17.
सही उत्तर चुनकर उसका औचित्य दीजिए:
ΔABC में, AB = 6\(\sqrt{3}\) सेमी, AC = 12 सेमी और BC = 6 सेमी है। कोण B है:
(A) 120°
(B) 60°
(C) 90°
(D) 45°
हल:
AC = 12 सेमी
AB = 6\(\sqrt{3}\) सेमी
BC = 6 सेमी
⇒ AB2 + BC2 = (6\(\sqrt{3}\))2 + (6)2
= 108 + 36
= 144 = (12)2 = AC2
अतः AB2 + BC2 = AC2
पाइथागोरस प्रमेय के विलोम से, ΔABC में,
∠B = 90°
अत: सही विकल्प (C) है।