JAC Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.1

Jharkhand Board JAC Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Exercise 12.1

(जब तक अन्यथा न कहा जाए, का प्रयोग कीजिए ।)

प्रश्न 1.
दो वृत्तों की त्रिज्याएँ क्रमशः 19 सेमी और 9 सेमी हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है।
हल :
दिया है पहले वृत्त की त्रिज्या (r₁) = 19 सेमी
∴ पहले वृत्त की परिधि = 2πr₁
= 2πr₁
= 2π × 19 = 38π सेमी
और दूसरे वृत्त की त्रिज्या (r₂) = 9 सेमी
∴ दूसरे वृत्त की परिधि = 2πr₂
= 2π × 9 = 18π सेमी
∴ दोनों वृत्तों की परिधियों का योग
= (38π + 18π)
= 56π सेमी
माना कि तीसरे वाँछित वृत्त की त्रिज्या r सेमी है।
प्रश्नानुसार,
वांछित वृत्त की परिधि = दोनों वृत्तों की परिधियों का योग
2πr = 56π
∴ r = \(\frac {56π}{2π}\) = 28 सेमी
अतः अभीष्ट वृत्त की त्रिज्या = 28 सेमी

प्रश्न 2.
दो वृत्तों की त्रिज्याएँ क्रमशः 8 सेमी और 6 सेमी हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसका क्षेत्रफल इन दोनों वृत्तों के क्षेत्रफलों के योग के बराबर है।
हल :
दिया है
पहले वृत्त की त्रिज्या (r₁) = 8 सेमी
∴ पहले वृत्त का क्षेत्रफल = πr₁²
= π × 8 × 8
= 64π वर्ग सेमी
और दूसरे वृत्त की त्रिज्या (r₂) = 6 सेमी
दूसरे वृत्त का क्षेत्रफल = πr₁²
∴ दोनों वृत्तों के क्षेत्रफलों का योग
= (64π + 36π)
= 100π वर्ग सेमी
माना कि तीसरे वाँछित वृत्त की त्रिज्या r सेमी है।
प्रश्नानुसार,
वाँछित वृत्त का क्षेत्रफल = दोनों वृत्तों का क्षेत्रफल
πr² = 100π
⇒ r² = 100
∴ r = \(\sqrt{100}\)
⇒ r = 10 सेमी
अतः अभीष्ट वृत्त की त्रिज्या = 10 सेमी

प्रश्न 3.
दी गई आकृति एक तीरंदाजी लक्ष्य को दर्शाती है, जिसमें केन्द्र से बाहर की ओर पाँच क्षेत्र GOLD, RED, BLUE, BLACK और WHITE चिह्नित हैं, जिनसे अंक अर्जित किए जा सकते हैं। GOLD अंक वाले क्षेत्र का व्यास 21 सेमी है तथा प्रत्येक अन्य पट्टी 10.5 सेमी चौड़ी है। अंक प्राप्त कराने वाले इन पाँचों क्षेत्रों में से प्रत्येक का क्षेत्रफल ज्ञात कीजिए।

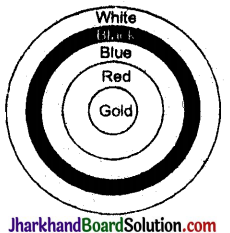
हल :
सबसे पहले GOLD क्षेत्र का व्यास = 21 सेमी
GOLD क्षेत्र की त्रिज्या (r₁) = \(\frac {21}{2}\) = 10.5 सेमी
∴ GOLD क्षेत्र का क्षेत्रफल = πr₁²
= \(\frac {22}{7}\) × 10.5 × 10.5 = 346.5 सेमी²
और अगली प्रत्येक पट्टी की चौड़ाई = 10.5 सेमी
तीरंदाजी के पाँच क्षेत्रों का क्रम = GOLD, RED, BLUE, BLACK, WHITE
∴ RED क्षेत्र की भीतरी त्रिज्या (r₁) = 10.5 सेमी
तब बाहरी त्रिज्या r₂ = r₁ + 10.5
= 10.5 + 10.5 = 21.0 सेमी
तब BLUE क्षेत्र की भीतरी त्रिज्या (r₂) = 21.0 सेमी
तथा बाहरी त्रिज्या r₃ = r₂ + 10.5 सेमी
= 21.0 + 10.5 = 31.5 सेमी
तब BLACK क्षेत्र की भीतरी त्रिज्या (r₃)
= 31.5 सेमी
तथा बाहरी त्रिज्या = r₄ = r₃ + 10.5 सेमी
= 31.5 + 10.5 = 42.0 सेमी
तब WHITE क्षेत्र की भीतरी त्रिज्या (r₄)
= 42.0 सेमी
तथा बाहरी त्रिज्या r₅ = r₄ + 10.5 सेमी
= 42.0 + 10.5 = 32.5 सेमी
∵ क्षेत्र वलयाकार हैं :
∴ RED क्षेत्र का क्षेत्रफल = πr₂² – πr₁²
= π[r²₂ – r₁²]
= π[(21)² – (10.5)²]
= \(\frac {22}{7}\) [441 – 110.25]
= \(\frac {22}{7}\) × 330.75 = \(\frac {7276.5}{7}\)
= 1039.5 सेमी²
BLUE क्षेत्र का क्षेत्रफल = πr₃² – πr₂²
= π[r₃² – r₂²]
= π[(31.5)² – (21)²]
= π(992.25 – 441)
= \(\frac {22}{7}\) × 551.25
= \(\frac {12127.5}{7}\)
= 1732.5 सेमी²
BLACK क्षेत्र का क्षेत्रफल = πr₄² – πr₃²
= π [(42)² – (31.5)²]
= π [1764 – 992.25]
= \(\frac {22}{7}\) × 771.75
= \(\frac {16978.5}{7}\)
= 2425.5 सेमी²
WHITE क्षेत्र का क्षेत्रफल = πr₅² – πr₄²
= π (r₄² – r₃²)
= π[(r₅)² – (r₄)²)
= π [(52.5)² – (42)²]
= \(\frac {22}{7}\) [2756.25 – 1764]
= \(\frac {22}{7}\) × 992.25
= \(\frac {21829.5}{7}\)
= 3118.5 सेमी²

प्रश्न 4.
किसी कार के प्रत्येक पहिए का व्यास 80 सेमी है। यदि यह कार 66 किमी प्रति घण्टे की चाल से चल रही है, तो 10 मिनट में प्रत्येक पहिया कितने चक्कर लगाता है ?
हल :
दिया है : कार के पहिए का व्यास = 80 सेमी
कार के पहिए की परिधि = π × व्यास
= \(\frac {22}{7}\) × 80
= \(\frac {1760}{7}\) सेमी
कार की चाल = 66 किमी / घण्टा
= 66 × \(\frac {1000}{60}\) मीटर / मिनट
= 66 × \(\frac {1000}{60}\) × 100 सेमी / मिनट
= 110000 सेमी / मिनट
∴ 10 मिनट में तय की गई दूरी = 110000 × 10
= 1100000 सेमी
∴ चक्करों की संख्या

अतः कार के प्रत्येक पहिए द्वारा 10 मिनट में लगाए गए चक्करों की संख्या = 4375

प्रश्न 5.
निम्नलिखित में सही उत्तर चुनिए तथा अपने उत्तर का औचित्य दीजिए:
यदि एक वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप से बराबर हैं, तो उस वृत्त की त्रिज्या है :
(A) 2 मात्रक
(B) मात्रक
(C) 4 मात्रक
(D) 7 मात्रक
हल :
वृत्त की परिधि = वृत्त का क्षेत्रफल
2πR = πR²
⇒ 2R = R²
∴ R = 2 मात्रक
अतः सही विकल्प A है