JAC Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.1

Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Exercise 8.1

प्रश्न 1.
ΔABC में, जिसका कोण B समकोण है, AB = 24 सेमी और BC = 7 सेमी है। निम्नलिखित का मान ज्ञात कीजिए :
(i) sin A, cos A,
(ii) sin C, cos C
हल:
समकोण ΔABC में,
∠B = 90°
पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (24)² + (7)²
= 576 + 49 = 625
AC = 25 सेमी

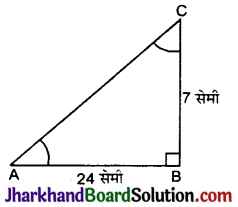
(i) समकोण ΔABC में,
sin A = \(\frac{A B}{A C}=\frac{7}{25}\)
और cos A = \(\frac{B C}{A C}=\frac{24}{25}\)

(ii) समकोण ΔABC में,
sin C = \(\frac{A B}{A C}=\frac{24}{25}\)
और cos C = \(\frac{B C}{A C}=\frac{7}{25}\)

प्रश्न 2.
चित्र में, tan P – cot R का मान ज्ञात कीजिए।

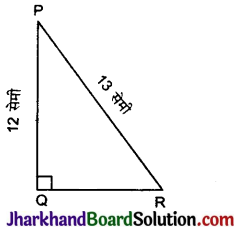
हल:
समकोण ΔPQR में, पाइथागोरस प्रमेय से,
PR² = QR² + PQ²
⇒ (13)² = QR² + (12)²
⇒ 169 = QR² + 144
⇒ QR² = 169 – 144
⇒ QR² = 25
⇒ QR = 5
tan P = \(\frac{Q R}{P Q}=\frac{5}{12}\)
और cot R = \(\frac{Q R}{P Q}=\frac{5}{12}\)
तब tan P – cot R = \(\frac{5}{12}-\frac{5}{12}\) = 0

प्रश्न 3.
sin A = \(\frac{3}{4}\) तो cos A और tan A के मान परिकलित कीजिए।
हल:
माना कि ABC एक समकोण Δ है जिसमें
∠B = 90°

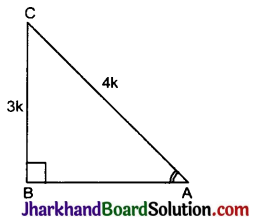
∠A के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC

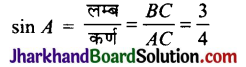
माना कि BC = 3k तथा AC = 4k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
⇒ (4k)² = AB² + (3k)²
⇒ 16k² = AB² + 9k²
⇒ AB² = 16k² – 9k²
⇒ AB² = 7k²
AB² = 7k²
AB = k\(\sqrt{7}\)


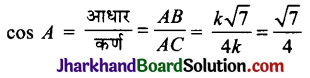
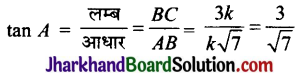
अतः cos A = \(\frac{\sqrt{7}}{4}\) तथा tan A = \(\frac{3}{\sqrt{7}}\)

प्रश्न 4.
यदि 15 cot A = 8 हो, तो sin A और sec A के मान ज्ञात कीजिए।
हल:
माना कि ABC एक समकोण Δ है, जिसमें ∠B = 90°.

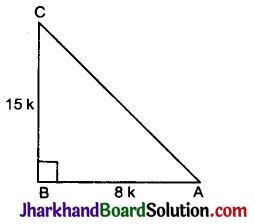
∠A के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC
15 cot A = 8 (दिया है)
⇒ cot A = \(\frac{8}{15}\)

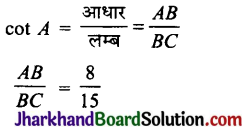
माना कि AB = 8k
तथा BC = 15k
समकोण ΔABC में,
AC² = AB² + BC²
= (8k)² + (15k)²
= 64k² + 225k²
= 289k²
AC = \(\sqrt{289 k^2}\)
∴ AC = 17k

प्रश्न 5.
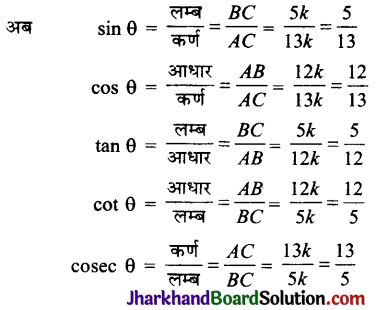
यदि sec θ = \(\frac{13}{12}\) हो, तो अन्य सभी त्रिकोणमितीय अनुपात परिकलित कीजिए।
हल:
माना कि ABC एक समकोण Δ है, जिसमें ∠B = 90° और ∠A = θ है।
∠θ के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC

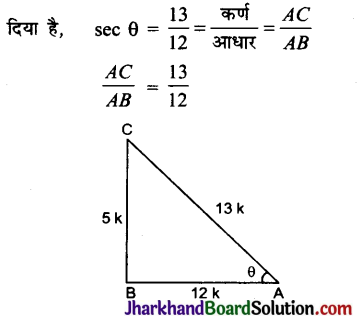
माना कि AC = 13k और AB = 12k
समकोण ΔABC में,
AC² = AB² + BC²
(13k)² = (12k)² + BC²
BC² = (13k)² – (12k)²
= 169k² – 144k² = 25k²
∴ BC = 5k

प्रश्न 6.
यदि ∠A और ∠B न्यूनकोण हैं, जहाँ cos A = cos B, तो दिखाइए कि ∠A = ∠B.
हल:
माना कि ABC एक समकोण Δ है, जिसमें कोण C = 90°, तब ∠A तथा ∠B न्यूनकोण होंगे।

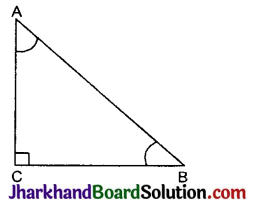
दिया है : cos A = cos B
⇒ \(\frac{A C}{A B}=\frac{B C}{A B}\)
⇒ AC = BC
ABC में, AC = BC
∵ ΔABC एक समद्विबाहु Δ है और बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
∴ ∠A = ∠B

प्रश्न 7.
यदि cot θ = \(\frac{7}{8}\), तो
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot² θ का मान निकालिए।
हल:
माना कि ABC एक समकोण त्रिभुज है, जिसमें ∠B = 90° और ∠A = θ है।
आधार = AB, लम्ब = BC तथा कर्ण = AC

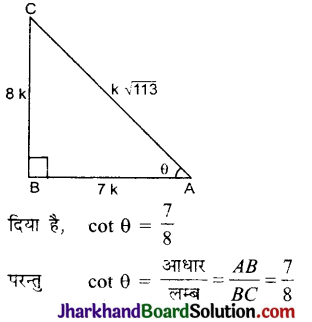
माना कि AB = 7k तथा BC = 8k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (7k)² + (8k)²
= 49k² + 64k² = 113k²
AC = ±\(\sqrt{113 k^2}\)
∴ AC = k\(\sqrt{113}\)
(∵ AC ≠ k\(\sqrt{113}\), क्योंकि भुजा ऋणात्मक नहीं हो सकती है)

[सूत्रः (a + b) (a – b) = a² – b² से]

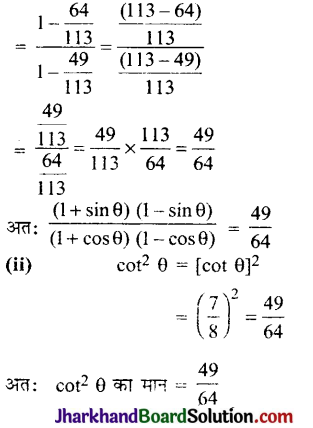
प्रश्न 8.
यदि 3 cot = A, तो जाँच कीजिए कि \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) = cos² A – sin² A है या नहीं।
हल:
माना कि ABC एक समकोण Δ है, जिसमें कोण B समकोण है।
∠A के लिए,
आधार = AB, लम्ब = BC तथा कर्ण = AC
दिया है, 3 cot A = 4
cot A = \(\frac{4}{3}\)

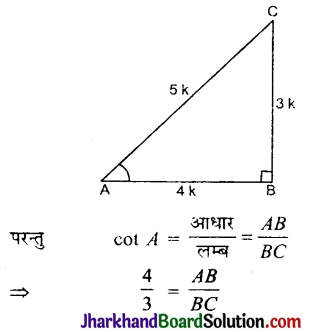
माना कि AB = 4k, BC = 3k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (4k)² + (3k)²
= 16k² + 9k² = 25k²
⇒ AC = ±\(\sqrt{25 k^2}\)
∴ AC = 5k
[∵ AC ≠ -5k, क्योंकि भुजा ऋणात्मक नहीं हो सकती है]

R.H.S. = cos² A – sin² A
= \(\left(\frac{4}{5}\right)^2-\left(\frac{3}{5}\right)^2\)
= \(\frac{16}{25}-\frac{9}{25}\)
= \(\frac{16-9}{25}=\frac{7}{25}\) …(2)
L.H.S. = R.H.S.
अर्थात् \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) = cos² A – sin² A

प्रश्न 9.
त्रिभुज ABC में, जिसका कोण B समकोण है, यदि tan A = \(\frac{1}{\sqrt{3}}\) तो निम्नलिखित के मान ज्ञात कीजिए:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
हल:
दिया है, एक ΔABC, जिसका कोण B समकोण

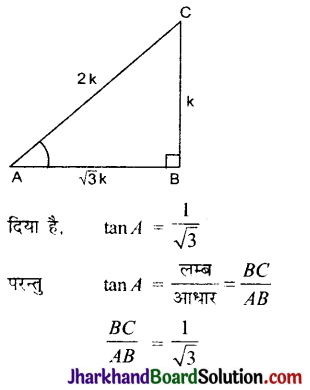
माना कि AB = \(\sqrt{3}\)k तथा BC = k
समकोण ΔABC में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (\(\sqrt{3}\)k)² + (k)²
= 3k² + k² = 4k²
⇒ AC = ±2k
∴ AC = 2k
(AC ≠ -2k, क्योंकि दूरी ऋणात्मक नहीं हो सकती)
∠A के लिए,
आधार = AB, लम्ब = BC, कर्ण = AC

प्रश्न 10.
ΔPQR में, जिसका कोण Q समकोण है, PR + QR = 25 सेमी और PQ = 5 सेमी है। sin P, cos P और tan P के मान ज्ञात कीजिए।
हल:
दिया है, ΔPQR में कोण Q समकोण है।

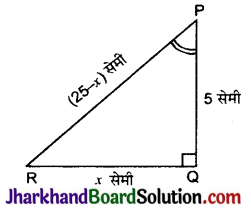
तथा PR + QR = 25 सेमी
PQ = 5 सेमी
माना कि QR = x सेमी
∴ PR = (25 – x) सेमी
अब समकोण ΔPQR में, पाइथागोरस प्रमेय से,
PR² = QR² + PQ²
(25 – x)² = (x)² + (5)²
625 – 50x + x² = x² + 25
– 50x = -600
x = \(\frac{-600}{-50}\) = 12 सेमी
∴ QR = 12 सेमी
PR = 25 – 12 = 13 सेमी

प्रश्न 11.
बताइए कि निम्नलिखित कथन सत्य हैं या असत्य। कारण सहित अपने उत्तर की पुष्टि कीजिए:
(i) tan A का मान सदैव 1 से कम होता है।
(ii) कोण A के किसी मान के लिए sec A = \(\frac{12}{5}\)
(iii) cos A, कोण A के cosecant के लिए प्रयुक्त एक संक्षिप्त रूप है।
(iv) cot A, cot और A का गुणनफल होता है।
(v) किसी भी कोण θ के लिए sin θ = \(\frac{4}{3}\)
हल:
(I) ∵ tan A = लम्ब / आधार
tan A का मान 1 से कम तभी हो सकता है, जब लम्ब, आधार से छोटा हो।
परन्तु ऐसा सदैव होना आवश्यक नहीं है।
अतः कथन असत्य है।

(ii) sec A = कर्ण / आधार = \(\frac{12}{5}\)
चूँकि sec A का मान सदैव 1 के बराबर या 1 से बड़ा होता है।
अतः कथन सत्य है।

(iii) ∵ cos A कोण A की cosine का संक्षिप्त रूप होता है, जबकि cosecant का अर्थ cosec A है।
अतः दिया हुआ कथन असत्य है।

(iv) cot A का अर्थ ∠A के cotangent से है।
स्वतन्त्र रूप में cot का कोई अस्तित्व ही नहीं है। अतः cot और A का गुणनफल कभी भी cot A नहीं हो सकता है।
अतः दिया हुआ कथन असत्य है।

(v) किसी समकोण त्रिभुज में कोण θ के लिए, यदि sin θ = \(\frac{4}{3}\), तो इसका अर्थ है कि θ की सम्मुख भुजा
और कर्ण का अनुपात 4 : 3 है।
परन्तु कर्ण, समकोण त्रिभुज की सबसे बड़ी भुजा होती है।
अतः दिया गया कथन असत्य है।