Students should go through these JAC Class 10 Maths Notes Chapter 6 त्रिभुज will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 10 Maths Notes Chapter 6 त्रिभुज
भूमिका :
सर्वांगसम आकृति के बारे में हम पिछली कक्षा IX में पढ़ चुके हैं। ऐसी दो ज्यामितीय आकृतियाँ जिनके आकार व रूप बिल्कुल समान हों एवं परस्पर अध्यारोपण पर एक-दूसरे को पूरा-पूरा ढक लेती हैं, सर्वांगसम आकृतियाँ कहलाती हैं।
इस अध्याय में हम ऐसी ही आकृतियों का अध्ययन करेंगे जिनका रूप या आकृतियाँ (Shape) बिल्कुल समान हों किन्तु आकार में भिन्नता हो, समरूप आकृतियाँ कहलाती हैं।
दो सर्वांगसम आकृतियाँ भी समरूप होती हैं। किन्तु इसका विलोम सर्वदा सत्य नहीं होता अर्थात् समरूप आकृतियाँ सदैव सर्वांगसम नहीं होती हैं।
→ बहुभुज (Polygon) : रेखाखण्डों से बनी साधारण वक्र बन्द आकृति को बहुभुज कहते हैं।
→ त्रिभुज (Triangle) : तीन भुजाओं वाले बहुभुज को त्रिभुज कहते हैं।
→ विषमबाहु त्रिभुज (Scalene Triangle) : एक त्रिभुज जिसकी तीनों भुजाएँ असमान हों, विषमबाहु त्रिभुज कहलाता है।
→ समद्विबाहु त्रिभुज (Isosceles Triangle) : एक त्रिभुज जिसकी कोई सी दो भुजाएँ समान हों, समद्विबाहु त्रिभुज कहलाता है।
→ समबाहु त्रिभुज (Equilateral Triangle) : एक त्रिभुज जिसकी तीनों भुजाएँ समान हों, समबाहु त्रिभुज कहलाता है।
→ न्यूनकोण त्रिभुज (Acute angled Triangle) : एक त्रिभुज जिसके तीनों कोण न्यून कोण ( less than 90°) हो, न्यूनकोण त्रिभुज कहलाता है।
→ अधिक कोण त्रिभुज (Obtuse angled Triangle) : एक त्रिभुज जिसका एक कोण अधिक कोण (greater than 90°) हो, अधिक कोण त्रिभुज कहलाता है।
→ समकोण त्रिभुज (Right angled Triangle) : एक त्रिभुज जिसका एक कोण समकोण है, समकोण त्रिभुज कहलाता है।
→ त्रिभुज का परिमाप (Perimeter of a Triangle) : त्रिभुज की तीनों भुजाओं का योग त्रिभुज का परिमाप कहलाता है।
→ त्रिभुज की माध्यिका (Median of a Triangle) : त्रिभुज के शीर्ष से इसके सम्मुख भुजा के मध्य बिन्दु को मिलाने वाली रेखा को त्रिभुज की माध्यिका कहते हैं।
→ त्रिभुज का शीर्षलम्ब (Altitude of a Triangle) : त्रिभुज के एक शीर्ष से सम्मुख भुजा पर खींची गयी लम्ब रेखा को त्रिभुज का शीर्षलम्ब कहते हैं।
→ त्रिभुज का कोण समद्विभाजक (Bisector of angle of a Triangle) : त्रिभुज के एक शीर्ष कोण को समद्विभाजित करने वाली रेखा को त्रिभुज का कोण समद्विभाजक कहते है।
→ समकोणीय त्रिभुज (Equiangular Triangle) : यदि दो त्रिभुजों के संगत कोण बराबर हों, तो वे समकोणीय त्रिभुज कहलाते हैं।
![]()
समरूप आकृतियाँ :
ऐसी आकृतियाँ जिनका आकार तो समान है, परन्तु माप भिन्न है, समरूप आकृतियाँ कहलाती हैं।
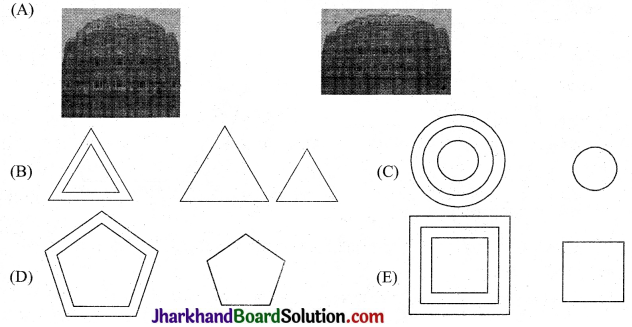
उदाहरण : चित्र (A) में दो भवन, चित्र (B) में चार त्रिभुज, चित्र (C) में चार वृत्त, चित्र (D) में तीन पंचभुज और चित्र (E) में चार वर्ग को देखने पर इनका आकार समान एवं माप भिन्न-भिन्न है अर्थात् सभी समान संख्या की भुजाओं के समबहुभुज हैं जैसे: समबाहु त्रिभुज, वर्ग, वृत्त, समपंचभुज इत्यादि समरूप होते हैं।
![]()
समरूप बहुभुज :
दो बहुभुज समरूप होते हैं, यदि उनके संगत कोण समान हों एवं उनकी संगत भुजाएँ समानुपाती हों।
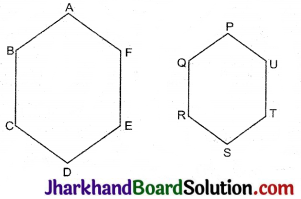
चित्र में, दो बहुभुज ABCDEF एवं PQRSTU समरूप हों, तो संगत कोण समान होंगे, अर्थात्
∠A = ∠P, ∠B = ∠Q, ∠C = ∠R, ∠D = ∠S, ∠E = ∠T एवं ∠F = ∠U
एवं संगत भुजाएँ समानुपाती होंगी, अर्थात्
\(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{C D}{R S}=\frac{D E}{S T}=\frac{E F}{T U}=\frac{F A}{U P}\)
टिप्पणी: यदि एक बहुभुज दूसरे बहुभुज के समरूप हो और दूसरा बहुभुज, तीसरे बहुभुज के समरूप हो, तो पहला बहुभुज, तीसरे बहुभुज के भी समरूप होता है।
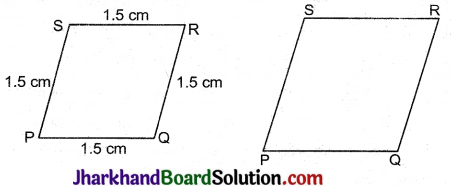
दो बहुभुजों के समरूप होने के लिए भुजाओं का समानुपाती होना ही पर्याप्त नहीं है, जैसे कि चित्र में, ABCD एक वर्ग है और PQRS एक समचतुर्भुज है। वर्ग ABCD की भुजाएँ समचतुर्भुज PQRS की भुजाओं की समानुपाती हैं परन्तु वर्ग ABCD के कोण समचतुर्भुज PQRS के कोणों के समान नहीं हैं। अतः वर्ग एवं समचतुर्भुज की भुजाएँ समानुपाती होते हुए भी दोनों समरूप नहीं हैं।
भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि
(i) सभी संगत कोण बराबर हों।
(ii) सभी संगत भुजाएँ एक ही अनुपात में (या समानुपाती हों।