Jharkhand Board JAC Class 10 Maths Important Questions Chapter 9 त्रिकोणमिति का अनुप्रयोग Important Questions and Answers.
JAC Board Class 10th Maths Important Questions Chapter 9 त्रिकोणमिति का अनुप्रयोग
लघुत्तरात्मक / निबन्धात्मक प्रश्न :
प्रश्न 1.
क्षैतिज तल पर किसी निश्चित बिन्दु से एक मीनार के शिखर का उन्नयन कोण 30° है। यदि प्रेक्षक 20 मीटर मीनार की ओर चलता है, तो मीनार के शिखर का उन्नयन कोण 15° बढ़ जाता है। मीनार की ऊँचाई ज्ञात करो ।
हल:
माना AB एक मीनार है जिसकी ऊँचाई h मीटर है। बिन्दु C से मीनार के शिखर का उन्नयन कोण 30° है। बिन्दु C से 20 मीटर मीनार की तरफ चलने पर मीनार के शिखर का उन्नयन कोण 15° बढ़ जाता है।
अर्थात् ∠ACB = 30° तथा ∠ADB = 45°
समकोण ΔABD में,
tan 45° = \(\frac{A B}{B D}\)
⇒ 1 = \(\frac{h}{B D}\)
⇒ BD = h मी. …..(1)
समकोण ΔABC में tan 30° = \(\frac{A B}{B C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{20+B D}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{20+h}\)
[ समी. (1) से BD = h]
20 + h = \(\sqrt{3}\)h
20 = \(\sqrt{3}\)h – h
20 = h(\(\sqrt{3}\) – 1)
h = \(\frac{20}{\sqrt{3}-1}\)
h = \(\frac{20(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}\)
h = \(\frac{20(\sqrt{3}+1)}{3-1}\)
h = 10(\(\sqrt{3}\) + 1) मीटर
अतः मीनार की ऊँचाई = 10 (\(\sqrt{3}\) + 1) मीटर ।
![]()
प्रश्न 2.
एक झील में पानी के तल से 20 मीटर ऊंचे बिन्दु A से, एक बादल का उन्नयन कोण 30° है। झील में बादल के प्रतिबिम्ब का A से अवनमन कोण 60° हैं। A से बादल की दूरी ज्ञात कीजिए।
हल:
माना कि BD पानी का तल है। B से 20 मीटर ऊँचे बिन्दु A से एक बादल (P) का उन्नयन कोण 30° है। माना झील में बादल के प्रतिबिम्ब की स्थिति C है तथा प्रतिबिम्ब इस प्रकार है कि झील में बादल के प्रतिबिम्ब का अवनमन कोण 60° है। माना कि PQ = h मी है।
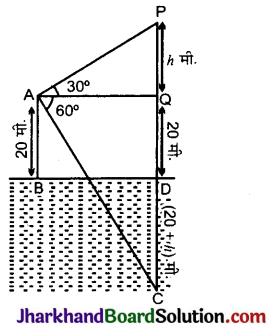
अतः ∠PAQ = 30° तथा ∠QAC = 60°
QD = AB = 20 मी
CD = PD = (20 + h) मी
QC = 20 + h + 20
= (40 + h) मी
BD = AQ
समकोण ΔPAQ में
tan 30° = \(\frac{P Q}{A Q}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{A Q}\)
⇒ AQ = h\(\sqrt{3}\) मीटर …..(1)
समकोण ΔAQC में
tan 60° = \(\frac{Q C}{A Q}\)
⇒ \(\sqrt{3}=\frac{40+h}{h \sqrt{3}}\)
[समीकरण (1) का प्रयोग करने पर]
⇒ 3h = 40 + h
⇒ 3h – h=40
⇒ 2h = 40
⇒ h = \(\frac{40}{2}\) = 20 मी
पुन: समकोण ΔPAQ में,
sin 30° = \(\frac{P Q}{A P}\)
⇒ \(\frac{1}{2}=\frac{h}{A Q}\)
⇒ \(\frac{1}{2}=\frac{20}{A Q}\) मीटर
AQ = 20 × 2
अतः A से बादल की दूरी = 40 मीटर ।
प्रश्न 3.
4000 मीटर की ऊँचाई पर उड़ते हुए वायुयान के ठीक नीचे जिस क्षण दूसरा वायुयान आता है, उसी क्षण क्षैतिज तल पर किसी बिन्दु से इन वायुयानों के उन्नयन कोण क्रमश: 60° और 45° हैं। उस क्षण पर दोनों वायुयानों के बीच की ऊर्ध्वाधर दूरी ज्ञात कीजिए।
हल:
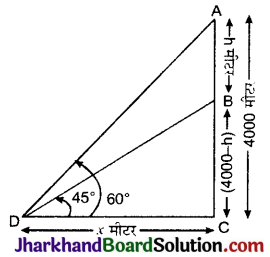
माना दो वायुयान A और B हैं जिनके बीच की ऊर्ध्वाधर दूरी AB = h मीटर
क्षैतिज तल पर स्थित बिन्दु D से इन वायुयानों A और B के उन्नयन कोण क्रमश: 60° और 450 हैं।
अर्थात् ∠ADC = 60° तथा ∠BDC = 45°
AC = 4000 मीटर
BC = AC – AB = (4000 – h) मीटर
समकोण ΔBCD में,
tan 45° = \(\frac{B C}{C D}\)
1 = \(\frac{4000-h}{x}\)
x = 4000 – h …..(i)
पुन: समकोण ΔACD में,
tan 60° = \(\frac{A C}{C D}\)
\(\sqrt{3}\) = \(\frac{4000}{x}\)
⇒ x\(\sqrt{3}\) = 4000
⇒ x = \(\frac{4000}{\sqrt{3}}\) …..(ii)
समीकरण (i) से x का मान रखने पर,
4000 – h = \(\frac{4000}{\sqrt{3}}\)
⇒ h = 4000 – \(\frac{4000}{\sqrt{3}}\)
⇒ h = 4000\(\left(1-\frac{1}{\sqrt{3}}\right)\)
⇒ h = 4000\(\left(\frac{\sqrt{3}-1}{\sqrt{3}}\right)\)
⇒ h = 4000\(\frac{4000 \times 0.732}{1.732}\)
⇒ h = \(\frac{2928}{1.732}\) = 1690.53 मीटर
अतः दोनों वायुयानों के बीच ऊर्ध्वाधर दूरी 1690.53 मीटर होगी।
![]()
प्रश्न 4.
धरातल के एक बिन्दु से एक हवाई जहाज का उन्नयन कोण 60° है। 15 सेकण्ड की उड़ान के पश्चात्, उन्नयन कोण 30° का हो जाता है। यदि हवाई जहाज एक निश्चित ऊँचाई 1500\(\sqrt{3}\) मीटर पर उड़ रहा हो, तो हवाई-जहाज की गति किमी / घंटा में ज्ञात कीजिए ।
हल:
माना P और Q हवाई जहाज की दो स्थितियाँ है। माना ABC एक क्षैतिज रेखा है जो A से जाती है।
दिया है कि स्थिति P और Q से, A बिन्दु से हवाई जहाज द्वारा बने उन्नयन कोण 30° तथा 60° है।
∴ ∠PAB = 60° और ∠QAC = 30°
इसी तरह, PB = QC = 1500\(\sqrt{3}\) मीटर
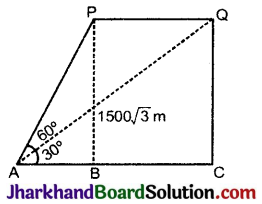
ΔABP में,
tan 60° = \(\frac{B P}{A B}\)
\(\sqrt{3}\) = \(\frac{1500 \sqrt{3}}{A B}\)
AB = 1500 मीटर
ΔACQ में,
tan 30° = \(\frac{Q C}{A C}\)
\(\frac{1}{\sqrt{3}}=\frac{1500 \sqrt{3}}{A C}\)
⇒ AC = 1500 × 3 = 4500 मीटर
∴ BC = AC – AB = 4500 – 1500
= 3000 मीटर
इस प्रकार हवाई जहाज 15 सेकण्ड में 3000 मीटर की दूरी तय करता है।
∴ हवाई जहाज की चाल = \(\frac{3000}{15}\) = 200 मी/से
= \(\frac{200 \times 60 \times 60}{1000}\)
= 720 किमी/ घण्टा
अतः हवाई जहाज की चाल 720 किमी/घण्टा है।
प्रश्न 5.
10 मीटर ऊँचे भवन के शिखर से एक टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टावर की ऊँचाई ज्ञात कीजिए।
हल:
माना AB एक टॉवर है उसी धरातल में एक भवन CD है जिसकी ऊँचाई 10 मीटर है।
टॉवर के शिखर का उन्नयन कोण और पाद का अवनमन कोण क्रमश: 60° और 45° है।
अर्थात् ∠ACE = 60°
और ∠ECB = 45°
BD || CE, CD || BE
CD = BE = 10 मी.
अब समकोण त्रिभुज CBD में,
tan 45° = \(\frac{C D}{D B}\)
\(1=\frac{10}{D B}\)
DB = 10 मी.
CE = DB = 10 मी.
पुनः समकोण त्रिभुज AEC में,
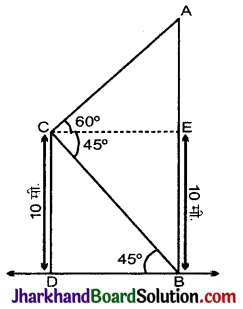
tan 60° = \(\frac{A E}{C E}=\frac{A E}{10}\)
AE = 10\(\sqrt{3}\) मी
अतः टॉवर AB की ऊँचाई
= AE + EB = 10\(\sqrt{3}\) + 10
= 10 (\(\sqrt{3}\) + 1) मीटर
अतः टॉवर AB की ऊँचाई = 10(\(\sqrt{3}\) + 1) मीटर
![]()
प्रश्न 6.
एक नदी के पुल के एक बिन्दु से नदी के सम्मुख किनारों के अवनमन कोण क्रमश: 30° और 45° है। यदि पुल किनारों से 4 मी की ऊँचाई पर है तो नदी की चौड़ाई ज्ञात कीजिए।
हल:
दिया है, नदी से पुल की ऊँचाई
AC = 4 मी
BC = x, CD = y
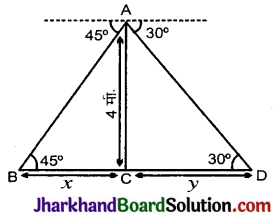
∴ समकोण ΔABC में,
\(\frac{A C}{B C}\) = tan 45°
⇒ \(\frac{4}{x}\) = 1 ⇒ x = 4 मी
पुन: समकोण ΔACD में,
\(\frac{A C}{C D}\) = tan 30°
⇒ \(\frac{4}{y}=\frac{1}{\sqrt{3}}\)
y = 4\(\sqrt{3}\) मी …..(ii)
समी. (i) व (ii) से,
∴ नदी की चौड़ाई (x + y)
= 4\(\sqrt{3}\) + 4
= 4(\(\sqrt{3}\) + 1)
= 10.92 मी ।
प्रश्न 7.
एक मीनार के पाद से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार के ऊँचाई 48 मी है तो भवन की ऊंचाई ज्ञात कीजिए।
हल:
माना AB एक मीनार है जिसके ऊँचाई 48 मी है तथा CD एक भवन है जिसकी ऊँचाई h मी है। दिया है, मीनार के पाद से भवन के शिखर का उन्नयन कोण 30° तथा भवन के पाद से मीनार के शिखर का उन्नयन कोण 60° है।
अर्थात् ∠CBD = 30°
तथा ∠ADB = 60°
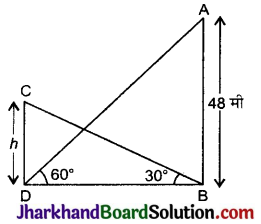
समकोण ΔCDB में,
tan 30° = \(\frac{C D}{B D}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{B D}\)
⇒ BD = h\(\sqrt{3}\) मी
पुन: समकोण ΔABD में,
tan 60° = \(\frac{A B}{B D}\)
\(\sqrt{3}\) = \(\frac{48}{h \sqrt{3}}\)
h = \(\frac{48}{\sqrt{3} \times \sqrt{3}}=\frac{48}{3}\)
= 16 मी
अतः भवन की ऊँचाई 16 मी है।
![]()
प्रश्न 8.
आँधी आने पर एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 60° का कोण बनाता है। पेड़ के पाद- बिंदु की दूरी जहाँ पेड़ का शिखर जमीन को छूता है, 3 मी है। पेड़ की ऊंचाई ज्ञात कीजिए।
हल:
माना आँधी से पहले पेड़ की लम्बाई BD है। आँधी के बाद पेड़ A स्थान से टूटकर पेड़ का शिखर जमीन पर C बिन्दु पर पड़ता है। टूटा हुआ भाग जमीन से 30° का कोण बनाता है।
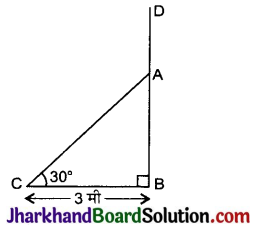
∴ ∠ACB = 30°
समकोण ΔABC में,
tan 30° = \(\frac{A B}{B C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{A B}{3}\)
⇒ AB = \(\frac{3}{\sqrt{3}}\) मी
पुन: समकोण ΔABC में,
cos 30° = \(\frac{B C}{A C}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{3}{A C}\)
⇒ AC = \(\frac{6}{\sqrt{3}}\) मी
पेड़ की कुल ऊँचाई = BD
= AB + AD
= AB + AC [∵ AD = AC]
= \(\left(\frac{3}{\sqrt{3}}+\frac{6}{\sqrt{3}}\right)\) मी
= \(\frac{9}{\sqrt{3}}\) मी = \(\frac{9 \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\)
= \(\frac{9 \sqrt{3}}{3}\) मी
= 3\(\sqrt{3}\) मी
प्रश्न 9.
अमित जो कि समतल जमीन पर खड़ा है, अपने से 200 मी दूर उड़ते हुए पक्षी का उन्नयन कोण 30° पाता है। दीपक जो कि 50 मी ऊँचे भवन की छत पर खड़ा है, उसी पक्षी का उन्नयन कोण 45° पाता है। अमित और दीपक पक्षी के विपरीत दिशा में हैं। दीपक से पक्षी की दूरी ज्ञात कीजिए।
हल:
माना अमित बिन्दु C पर खड़ा है तथा AB चिड़िया की धरातल पर स्थित बिन्दु B से ऊँचाई है तथा माना दीपक बिन्दु D पर स्थित है, जहाँ DE भवन की ऊँचाई है।
दिया है, ∠ACB = 30°, ∠ADF = 45° तथा DE = 50 मी
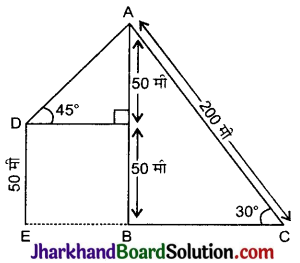
अब, समकोण ΔABC में,
sin 30° = लम्ब / कर्ण
= \(\frac{A B}{A C}\)
\(\frac{1}{2}=\frac{A B}{200}\)
AB = 100 मी
समकोण ΔAFD में,
sin 45° = लम्ब / कर्ण
= \(\frac{A F}{A D}\)
(AB = AF + BF
100 = AF + 50
AF = 50 मी)
= \(\frac{1}{\sqrt{2}}=\frac{50}{A D}\)
AD = 50\(\sqrt{2}\) मी
अतः दीपक की चिड़िया से दूरी 50\(\sqrt{2}\) मी है।
![]()
प्रश्न 10.
एक ऊर्ध्वार मीनार क्षैतिज तल पर खड़ी है तथा उसके ऊपर एक 6 मी ऊँचा झंडा लगा है। तल के किसी बिन्दु से झंडे के पाद तथा शिखर के उन्नयन कोण क्रमश: 30° तथा 45° है। मीनार की ऊँचाई ज्ञात कीजिए। (\(\sqrt{3}\) = 1.732 लीजिए)
हल:
माना AB एक मीनार है तथा BC झंडा है। अब माना कि P भूमि पर एक ऐसा बिन्दु है, जिसका मीनार के शिखर का उन्नयन कोण ∠APB = 30° तथा मीनार पर स्थित झंडा का उन्नयन कोण ∠APC = 45° है तथा BC = 6 मी अब माना AB = h मी तथा PA = x मी
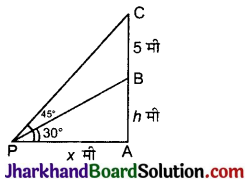
समकोण ΔPAB से,
cos 30° = \(\frac{P A}{P B}=\frac{x}{h}\)
\(\sqrt{3}=\frac{x}{h}\) (∵ cot 30° = \(\sqrt{3}\))
x = \(\sqrt{3}\)h …..(i)
समकोण ΔPAC से,
cot 45° = \(\frac{x}{h+6}=\frac{P A}{A C}\) (∵ cot 45° = 1)
x = h + 6 ….. (ii)
समीकरण (i) व (ii) से,
\(\sqrt{3}\)h = h + 6
\(\sqrt{3}\)h – h = 6
= \(\frac{6}{\sqrt{3}-1}\)
= \(\frac{6}{1.732-1}\)
= \(\frac{6}{0.732}\)
= \(\frac{6000}{732}\)
= 8.19 मी
अतः मीनार की ऊँचाई 8.19 मी है।
प्रश्न 11.
100 मी ऊंचे एक लाइट हाउस से दूर एक नाव को ले जाता हुआ व्यक्ति 2 मिनट में लाइट हाउस में शिखर का उन्नयन कोण को 60° से 30° बढ़लता हुआ पाता है। मीटर प्रति मिनट में नाव की चाल ज्ञात कीजिए। (\(\sqrt{3}\) = 1.732 लीजिए)
हल:
माना AB एक 100 मी ऊँचाई का लाइट हाउस है प्रारम्भ में व्यक्ति C बिन्दु पर था तथा 2 मिनट बाद D बिन्दु पर आता है।
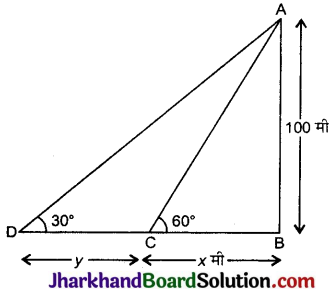
यहाँ, ∠ACB = 60° तथा ∠ADB = 30° है। माना BC = x मी तथा BD = y मी है।
समकोण ΔABC में,
tan 60° = \(\frac{A B}{B C}\)
\(\sqrt{3}=\frac{100}{x}\)
x = \(\frac{100}{\sqrt{3}}\) ……..(i)
पुन: समकोण ΔABD में,
tan 30° = \(\frac{A B}{B D}\)
\(\frac{1}{\sqrt{3}}=\frac{100}{B D}\)
BD = 100\(\sqrt{3}\)
BC + CD = 100\(\sqrt{3}\)
x + y = 100\(\sqrt{3}\) …..(ii)
समीकरण (i) से, x = \(\frac{100}{\sqrt{3}}\) समीकरण (ii) में रखने पर,
\(\frac{100}{\sqrt{3}}\) + y = 100\(\sqrt{3}\)
y = \(100 \sqrt{3}-\frac{100}{\sqrt{3}}\)
= \(\frac{300-100}{\sqrt{3}}\)
y = \(\frac{200}{\sqrt{3}}\) मी
बिन्दु C से D तक जाने मैं नाव द्वारा लगा समय 2 मिनट है।
तथा CD = \(\frac{200}{\sqrt{3}}\)
अतः नाव को चाल = समय / दूरी
\(\frac{C D}{2}\) ⇒ \(\frac{y}{2}\)
= \(=\frac{200}{\sqrt{3} \times 2}\) (∵ y = \(\frac{200}{\sqrt{3}}\) मी)
= \(\frac{100}{\sqrt{3}}=\frac{100}{1.732}\)
= 57.73 मीटर / मिनट
![]()
प्रश्न 12.
एक मीनार के पाद से गुजरने वाली सीधी रेखा पर पाद से क्रमशः 4 मी तथा 16 मी की दूरियों पर दो बिंदु C व D स्थित हैं। यदि C व D से मीनार के शिखर के उन्नयन कोण एक-दूसरे के पूरक हों, तो मीनार की ऊँचाई ज्ञात कीजिए।
हल:
माना मीनार की ऊँचाई = h मीटर
ΔABC में, \(\frac{A B}{B C}\) = tan(90° – θ)
\(\frac{h}{4}\) = cot θ …..(i)
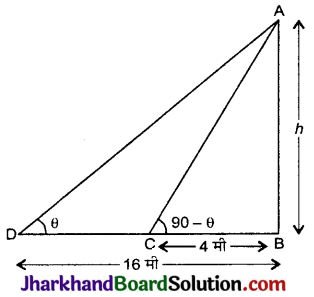
ΔABD में,
\(\frac{A B}{B D}\) = tan θ
\(\frac{h}{16}\) = tan θ …..(ii)
समीकरण (i) और (ii) का गुणा करने पर,
\(\frac{h}{4} \times \frac{h}{16}\) = cot θ × tan θ
\(\frac{h^2}{64}=1\)
[∵ cot θ × tan θ = \(\frac{1}{\tan \theta}\) × tan θ = 1]
⇒ h2 = 64
⇒ h = 8 मी
अतः मीनार की ऊँचाई 8 मीटर है।
प्रश्न 13.
एक हवाई जहाज भूतल से ऊपर 300 मी की ऊँचाई पर उड़ रहा है। इस ऊँचाई पर उड़ते हुए हवाई जहाज से एक नदी के दोनों किनारों पर परस्पर विपरीत दिशाओं में स्थित दो बिंदुओं के अवनमन कोण क्रमशः 45° तथा 60° हैं। नदी की चौड़ाई ज्ञात कीजिए। [\(\sqrt{3}\) = 1.732 प्रयोग कीजिए]
हल:
माना हवाई जहाज A बिंदु पर नदी से 300 मीटर ऊँचाई पर है। C व D नहीं के विपरीत किनारों पर है।
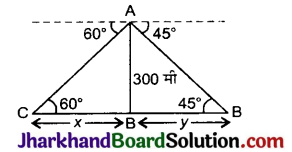
समकोण ΔABC में,
\(\frac{B C}{A B}\) = cot 60°
⇒ \(\frac{x}{300}=\frac{1}{\sqrt{3}}\)
⇒ x = \(\frac{300}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= 100\(\sqrt{3}\) मी
= 100 × 1.732 = 173.2 मी
समकोण ΔABD में,
⇒ \(\frac{B D}{A B}\) = cot 45°
⇒ \(\frac{y}{300}\) = 1
⇒ y = 300
नदी को चौड़ाई = x + y
= 173.2 + 300
= 473.2 मी
प्रश्न 14.
समुद्र तल से 75 मी. ऊँचे लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° तथा 45° है। यदि दोनों जहाज लाइट हाउस की विपरीत दिशाओं में हो, तो दोनों जहाजों के बीच की दूरी ज्ञात कीजिए।
हल:
माना AB लाइट हाउस है।
जहाज क्रमश: बिन्दु C व D पर है।
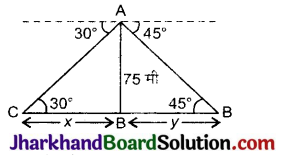
समकोण ΔABC में,
⇒ \(\frac{A B}{B C}\) = tan 30°
⇒ \(\frac{75}{x}=\frac{1}{\sqrt{3}}\)
⇒ x = 75\(\sqrt{3}\) मी
समकोण ΔABD में,
⇒ \(\frac{A B}{B D}\) = tan 30°
⇒ \(\frac{75}{y}\) = 1
y = 75 मी
जहाजों के बीच की दूरी = x + y
= (75\(\sqrt{3}\) + 75) मी
= 75(\(\sqrt{3}\) + 1) मी
![]()
प्रश्न 15.
एक झील के पानी की सतह में 60 मी ऊँचाई पर स्थित एक बिन्दु से बादल का उन्नयन कोण 30° है, तथा झील के पानी में बादल का परछाई का अवनमन कोण 60° है। बादल की झील के पानी की सतह से ऊँचाई प्राप्त कीजिए।
हल:
ΔCMP में,
tan 30° = \(\frac{C M}{P M}\)
\(\frac{1}{\sqrt{3}}=\frac{h}{P M}\) या PM = \(\sqrt{3}\)h …….(i)
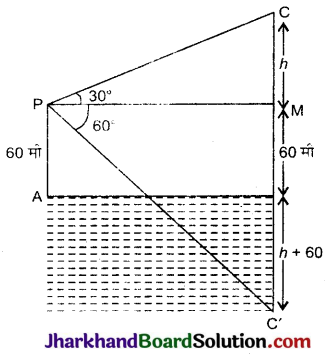
ΔPMC में,
tan 60° = \(\frac{C M}{P M}\)
= \(\frac{h+60+60}{P M}=\sqrt{3}\)
या PM = \(\frac{h+120}{\sqrt{3}}\) …..(ii)
समीकरण (i) और (ii) से,
\(\sqrt{3}\)h = \(\frac{h-120}{\sqrt{3}}\)
3h = h + 120
2h = 120 ⇒ h = 60 मी
पानी के तल से बादल की ऊँचाई = h + 60
= 60 + 60 = 120 मी
प्रश्न 16.
एक मीनार के एक ही ओर तथा इसके आध र से एक ही सरल रेखा में दो बिंदु A तथा B हैं। मीनार के शिखर से इन बिंदुओं अवनमन कोण क्रमश: 60° व 45° हैं। यदि मीनार की ऊँचाई 15 मी हो, तो इन बिंदुओं के बीच की दूरी ज्ञात कीजिए।
हल:
माना PT एक मीनार है।
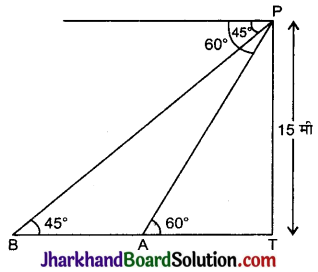
समकोण ΔPTA में,
tan 60° = \(\frac{P T}{T A}\)
⇒ \(\sqrt{3}=\frac{15}{T A}\)
⇒ TA = \(\frac{15}{\sqrt{3}}\)
पुन: समकोण ΔPTB में,
tan 45° = \(\frac{P T}{T B}\)
⇒ 1 = \(\frac{15}{T B}\)
⇒ TB = 15 मी
बिन्दुओं A व B के बीच की दूरी
AB = TB – TA
= 15 – \(\frac{15}{\sqrt{3}}\) = 15\(\left(\frac{\sqrt{3}-1}{\sqrt{3}}\right)\) मी
प्रश्न 17.
एक नदी के एक किनारें पर खड़ा एक व्यक्ति, नदी के दूसरे किनारे पर खड़े एक वृक्ष के शिखर का उन्नयन कोण 60° पाता है जब वह किनारे से 30 मी दूर जाता है, तो वह उन्नयन कोण 30° पाता है। वृक्ष की ऊँचाई तथा नदी की चौड़ाई ज्ञात कीजिए। [\(\sqrt{3}\) = 1.732 प्रयोग कीजिए]
हल:
माना नदी के एक किनारे पर एक वृक्ष AB है तथा नदी के दूसरे किनारे पर व्यक्ति P बिंदु पर है। यहाँ AP नदी की चौड़ाई है।
जब व्यक्ति P से बिंदु M पर जाता है, तो उन्नयन कोण 60° से 30° हो जाता है।
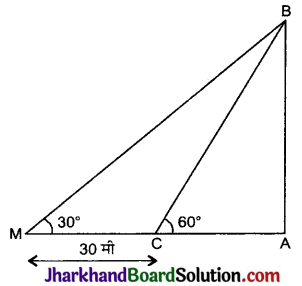
समकोण ΔPAB में,
⇒ tan 60° = \(\frac{A B}{P A}\)
⇒ \(\sqrt{3}\) = \(\frac{A B}{P A}\)
⇒ AB = \(\sqrt{3}\)PA …..(i)
पुन: समकोण ΔMAB में,
tan 30° = \(\frac{A B}{M A}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{A B}{30+A P}\)
⇒ 30 + AP = \(\sqrt{3}\)AB
⇒ 30 + AP = \(\sqrt{3}\)(\(\sqrt{3}\)AP) [समी (i) से]
⇒ 30 + AP = 3AP
⇒ 2AP = 30
⇒ AP = 15 मी.
समीकरण (i) से,
AB = \(\sqrt{3}\) × 15 = 15\(\sqrt{3}\) मी
अतः नदी की चौड़ाई = 15 मी
तथा पेड़ की ऊँचाई = 15\(\sqrt{3}\) मी
![]()
प्रश्न 18.
भूमि पर स्थित बिंदु A से एक हवाई जहाज का उन्नयन कोण 60° है। 10 सैकंड की उड़ान के बाद उसी ऊँचाई पर उड़ते हुए हवाई जहाज का उन्नयन कोण बिंदु A से 30° हो जाता है। यदि हवाई जाहज की औसत चाल 720 किमी / घंटा हो, तो हवाई जाहज की धरती से स्थिर ऊँचाई ज्ञात कीजिए।
हल:
माना P और Q हवाई जहाज की दो स्थितियाँ है। माना ABC एक क्षैतिज रेखा है जो A से जाती है।
∵ हवाई जाहज द्वारा 1 घंटे में तय दूरी,
PQ = 720 किमी
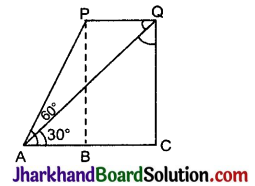
∵ हवाई जहाज द्वारा 1 सकण्ड में तय दूरी
= \(\frac{720 \times 1000}{60 \times 60}\) मी
= 200 मी
और 10 सेकंड में तय दूरी = 10 × 200 मी = 2000 मी
∴ PQ = 2000 मी
समकोण ΔABP में
tan 60° = \(\frac{P B}{A B}\)
⇒ \(\sqrt{3}=\frac{P B}{A B}\)
⇒ PB = \(\sqrt{3}\)AB …..(i)
⇒ tan 30° = \(\frac{Q C}{A C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{Q C}{A C}\)
⇒ AC = \(\sqrt{3}\)QC
⇒ AB + BC = \(\sqrt{3}\)PB [∵ QC = PB]
⇒ AB + 200 = \(\sqrt{3}\) × \(\sqrt{3}\)AB
[∵ PQ = 2000
[तथा PB = \(\sqrt{3}\)AB]
⇒ AB + 2000 = 3AB
⇒ 2AB = 2000
⇒ AB = 1000 मी
समीकरण (i) से
PB = \(\sqrt{3}\) × 1000
= 1000\(\sqrt{3}\) मी
अतः हवाई जहाज की धरती से स्थिर ऊँचाई 1000\(\sqrt{3}\) मी है।
वस्तुनिष्ठ प्रश्न :
रिक्त स्थानों की पूर्ति कीजिए :
प्रश्न (क).
- यदि कोई प्रेक्षक किसी वस्तु को देख रहा है, तो प्रेक्षक की आँख को उस वस्तु से मिलाने वाली क्षैतिज रेखा को ……………. रेखा कहते हैं।
- वह रेखा, जो प्रेक्षक की आँख से सीधी भूमि के समांतर जाती है, ……………… रेखा कहलाती है।
- जब प्रेक्षक किसी वस्तु को देखने के लिए अपने सिर को ऊपर उठाता है, तो वस्तु प्रेक्षक की आँख पर ………………. कोण बनाती है।
- जब प्रेक्षक किसी वस्तु को देखने के लिए अपना सिर नीचे झुकता है, तो वस्तु की आँख पर कोण ……………… बनाती है।
- उन्नयन कोण एवं अवनमन कोण सदैव बराबर और ……………… कोण होते हैं।
उत्तर:
- दृष्टि,
- क्षैतिज,
- उन्नयन,
- अवनमन,
- न्यून ।
![]()
निम्न में सत्य / असत्य ज्ञात कीजिए :
प्रश्न (ख).
- अवनमन कोण को अवनति कोण भी कहते हैं।
- उन्नयन कोण एवं अवनमन कोण एकांतर कोण होते हैं।
- उन्नयन कोण सदैव अधिक कोण होता है।
- अवनमन कोण सदैव समकोण होता है।
- त्रिकोणमिति की सहायता से दूरियों तथा ऊँचाइयों की गणना सरलता से की जा सकती है।
उत्तर:
- सत्य,
- सत्य,
- असत्य,
- असत्य,
- सत्य ।
(ग) बहुविकल्पीय प्रश्न :
प्रश्न 1.
एक सीधी खड़ी छड़ की लंबाई तथा उसकी परछाई में 1 : \(\sqrt{3}\) का अनुपात है। उस समय सूर्य का उन्नयन कोण ज्ञात कीजिए:
(A) 30°
(B) 60°
(C) 45°
(D) 90°
हल:
माना छड़ की लंबाई AB तथ उसकी परछाई BC है।
माना उन्नयन कोण θ है।
दिया है, BA : BC = 1 : \(\sqrt{3}\)
⇒ \(\frac{B A}{B C}=\frac{1}{\sqrt{3}}\)
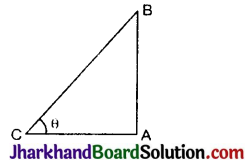
समकोण ΔCAB में
sin θ = \(\frac{A B}{B C}\)
⇒ sin θ = \(\frac{1}{\sqrt{3}}\)
⇒ sin θ = sin 60°
⇒ θ = 60°
अत: सही विकल्प (B) है।
प्रश्न 2.
निम्न आकृति में वस्तु 1 को बिंदुओं O1 तथा O2 से देखने पर बने अवनमन कोण क्रमश: हैं:
(A) 45°, 75°
(B) 60°, 90°
(C) 30°, 60°
(D) 45°, 30°
हल:
एक रेखा PO1 इस प्रकार खींची कि PO1 || AC
यहाँ ∠PO1A + ∠AO1C = 90°
⇒ ∠PO1A + 60° = 90°
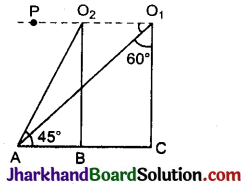
⇒ ∠PO1A = 90° – 60° = 30°
अब ∠PO2A = ∠O2AB = 45° (एकान्तर कोण)
O1 से अवनमन कोण = 30°
O2 से अवनमन कोण = 45°
अत: सही विकल्प (D) है।
![]()
प्रश्न 3.
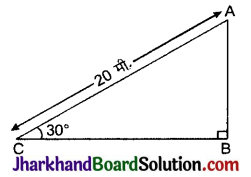
निम्न आकृति में अच्छी तरह से तनी हुई एक 20 मी लम्बी रस्सी भूमि पर सीधे लगे खंभे के शिखर से बंधी है। यदि भूमि स्तर के साथ रस्सी द्वारा बनाया गया कोण 30° का है, तो खंभे की ऊँचाई ज्ञात कीजिए।
(A) 10 मी
(B) 20 मी
(C) 40 मी
(D) 50 मी
हल:
समकोण ΔBAC में.
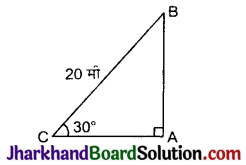
sin 30° = \(\frac{A B}{B C}\)
⇒ \(\frac{1}{2}=\frac{A B}{20}\)
⇒ \(\frac{20}{2}\) मी = 10 मी
अत: सही विकल्प (A) है।
प्रश्न 4.
निम्न आकृति में, भूमि के एक बिन्दु C से, जो मीनार के पाद बिन्दु से 60 मी की दूरी पर है, मीनार AB के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई है :
(A) 60\(\sqrt{3}\) मी.
(B) 60 मी
(C) 20\(\sqrt{3}\) मी
(D) 20 मी
हल:
समकोण ΔABC में,
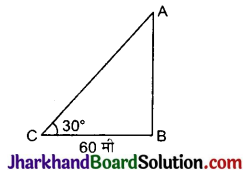
tan 30° = \(\frac{A B}{B C}\)
\(\frac{1}{\sqrt{3}}=\frac{A B}{60}\)
AB = \(\frac{60}{\sqrt{3}}=\frac{60 \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\)
\(\frac{60 \sqrt{3}}{3}\) = 20\(\sqrt{3}\) मी
अत: सही विकल्प (C) है।
प्रश्न 5.
एक मीनार के आधार से 100 मीटर की दूरी पर स्थित बिन्दु से उसके शिखर का उन्नयन कोण 45° है। मीनार की ऊँचाई है:
(A) 50 मीटर
(B) 100 मीटर
(C) \(\frac{100}{\sqrt{2}}\) मीटर
(D) \(\frac{100 \times \sqrt{3}}{2}\) मीटर
हल:
माना मीनार की ऊँचाई (BC)h मीटर है।
मीनार के आधार से 100 मीटर दूरी पर स्थित बिन्दु उसके शिखर का उन्नयन कोण 45° है। अर्थात् AB = 100 मी. तथा ∠CAB = 45°
समकोण ΔABC में,
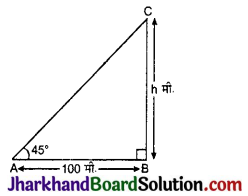
tan 45° = \(\frac{B C}{A B}\)
⇒ 1 = \(\frac{h}{100}\)
∴ h = 100 मीटर
अतः मीनार की ऊँचाई = 100 मी.
सही विकल्प (B) है।
![]()
प्रश्न 6.
15 मी लम्बी एक सीढ़ी एक ऊर्ध्वाधर दीवार के शिखर तक पहुँचती है। यदि यह सीढ़ी दीवार के साथ 60° का कोण बनाती है, तो दीवार की ऊँचाई है :
(A) 15\(\sqrt{3}\) मी.
(B) \(\frac{15 \sqrt{3}}{2}\) मी.
(C) \(\frac{15}{2}\) मी.
(D) 15 मी.
हल:
माना कि AB एक ऊर्ध्वाधर दीवार है जिसकी ऊँचाई 1⁄2 मी. है। माना कि AC एक सीढ़ी है जो दीवार के शिखर तक पहुँचती है तथा सीढ़ी की लम्बाई 15 मी. है। सीढ़ी दीवार के साथ 60° का कोण बनाती है, तब
∠ACB = 60° तथा AC = 15 मी.
समकोण ΔABC में,
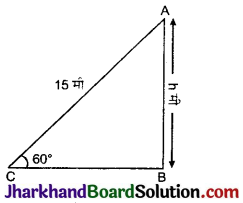
sin 60° = \(\frac{A B}{A C}\)
\(\frac{\sqrt{3}}{2}=\frac{h}{15}\)
h = \(\frac{15 \sqrt{3}}{2}\) मी.
अत: विकल्प (B) सही है।
प्रश्न 7.
6 मीटर ऊँचे एक खम्भे की छाया 2\(\sqrt{3}\) मीटर लम्बी हो तो सूर्य का उन्नतांश कोण है:
(A) 60°
(B) 45°
(C) 30°
(D) 90°
हल:
माना कि AB एक खम्भा है जिसकी ऊँचाई 6 मीटर है।
खम्भे की छाया की लम्बाई (BC) = 2\(\sqrt{3}\) मीटर
माना कि सूर्य का उन्नतांश कोण (∠ACB) = θ
अत: समकोण ΔABC में
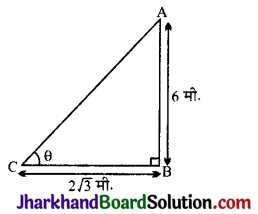
tan θ = \(\frac{A B}{B C}\)
⇒ tan θ = \(\frac{6}{2 \sqrt{3}}\)
⇒ tan θ = \(\sqrt{3}\)
⇒ tan θ = tan 60°
⇒ θ = 60°
अत: सही विकल्प (A) है।
प्रश्न 8.
किसी मीनार की छाया उसकी ऊँचाई के बराबर हो तो सूर्य का उन्नयन कोण है:
(A) 90°
(B) 60°
(C) 45°
(D) 30°
हल:
माना BC कोई मीनार है, जिसकी ऊँचाई / मीटर है।
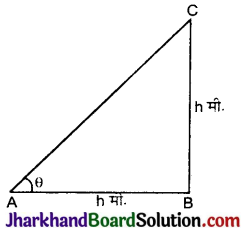
इसकी छाया AB, h मीटर होगी।
पुनः माना सूर्य का उन्नयन कोण ∠CAB = θ
समकोण ΔABC में,
tan θ = \(\frac{B C}{A B}=\frac{h}{h}\)
⇒ tan θ = 1
⇒ tan θ = tan 45°
∴ θ = 45°
अतः सही विकल्प (C) है।
![]()
प्रश्न 9.
10 मीटर ऊँची एक मीनार के शिखर से पृथ्वी पर एक बिन्दु का अवनमन कोण 30° है। बिन्दु की मीनार के आधार से दूरी है:
(A) 10 \(\sqrt{3}\) मीटर
(B) \(\frac{10}{\sqrt{3}}\) मीटर
(C) 10 मीटर
(D) 5\(\sqrt{3}\) मीटर
हल:
माना AC कोई मीनार है जिसकी ऊँचाई 10 मीटर है।
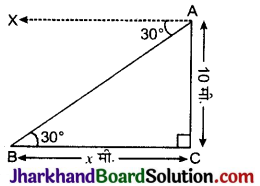
माना मीनार के आधार से बिन्दु की दूरी (BC) = x मीटर
मीनार के शिखर से पृथ्वी पर एक बिन्दु का अवनमन कोण 30° है।
∴ ∠XAB = 30°
∠XAB = ∠ABC = 30° (एकान्तर कोण)
समकोण ΔACB में,
tan 30° = \(\frac{A C}{B C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{10}{x}\)
∴ x = 10\(\sqrt{3}\) मीटर
अतः बिन्दु की मीनार के आधार से दूरी 10\(\sqrt{3}\) मीटर होगी सही विकल्प (A) है।
प्रश्न 10.
एक पतंग भूमि से 30 मी की ऊँचाई पर 60 मी लंबी डोरी की सहायता से उड़ रही है। यह मानते हुए कि डोरी में कोई ढील नहीं है, पतंग का भूमि पर उन्नयन कोण है:
(A) 45°
(B) 30°
(C) 60°
(D) 90°
हल:
माना कि भूमि से 30 मीटर की ऊँचाई पर पतंग की स्थिति है जोकि 60 मीटर लंबी डोरी (AC) की सहायता से उड़ रही है। माना कि पतंग की डोरी का क्षैतिज के साथ कोण θ है।
अर्थात् ∠ACB = θ
समकोण ΔABC में,
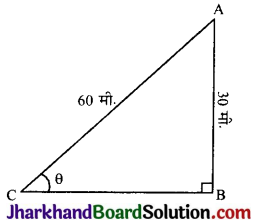
sin θ = \(\frac{A B}{A C}\)
⇒ sin θ = \(\frac{30}{60}\)
⇒ sin θ = \(\frac{1}{2}\)
⇒ sin θ = sin 30°
⇒ θ = 30°
अतः विकल्प (B) सही है।
![]()
प्रश्न 11.
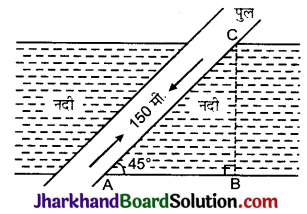
एक नदी के ऊपर एक पुल नदी के तट के साथ 45° का कोण बनाता है। यदि नदी के ऊपर पुल की लम्बाई 150 मीटर है, तो नदी की चौड़ाई क्या होगी:
(A) 75\(\sqrt{2}\) मीटर
(B) 50\(\sqrt{2}\) मीटर
(C) 75 मीटर
(D) 150 मीटर
हल:
माना AC पुल है जिसकी लम्बाई 150 मीटर है
तथा BC नदी की चौड़ाई है। पुल नदी के साथ 45° का कोण बनाता है।
अर्थात् ∠CAB = 45°
समकोण ΔABC में,
sin 45° = \(\frac{B C}{A C}\)
\(\frac{1}{\sqrt{2}}=\frac{B C}{150}\)
BC = \(\frac{150}{\sqrt{2}}\)
BC = \(\frac{150 \sqrt{2}}{\sqrt{2} \times \sqrt{2}}\)
BC = 75\(\sqrt{2}\)
अतः नदी की चौड़ाई 75\(\sqrt{2}\) मीटर होगी।
सही विकल्प (A) है।