Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.1 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Exercise 8.1
Question 1.
In ΔABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A, (ii) sin C, cos C.
Solution :
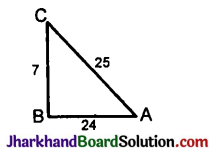
(i) sin A, cos A
AC² = AB² + BC²
= 24² + 7² = 576 + 49
= 625
∴ AC = 25

![]()
Question 2.
In the figure, find tan P – cot R.
Solution :
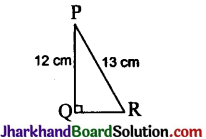
QR² = PR² – PQ² = 13² – 12²
= 169 – 144 = 25.
∴ QR = 5.
tan P = \(\frac{\mathrm{QR}}{\mathrm{PQ}}=\frac{5}{12}\)
cot R = \(\frac{\mathrm{QR}}{\mathrm{QP}}=\frac{5}{12}\)
∴ tan P – cot R = \(\frac{5}{12}=\frac{5}{12}\) = 0
Question 3.
If sin A = \(\frac{3}{4}\), calculate cos A and tan A.
Solution:
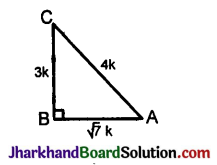
Given, sin A = \(\frac{3}{4}\) ⇒ \(\frac{P}{H}\) = \(\frac{3}{4}\)
Let P = 3k and H = 4k.
In right angled ΔABC,
P² + B² = H² (By Pythagoras theorem)
⇒ (3k)² + B² = (4k)²
⇒ 9k² + B² = 16k²
⇒ B² = 16k² – 9k² = 7k²
∴ B = +k\(\sqrt{7}\) (∵ Base cannot be -ve)
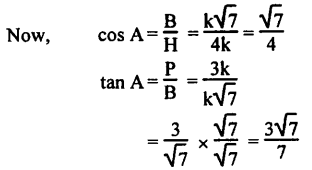
![]()
Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:
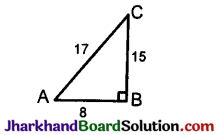
Given, 15 cot A = 8 ⇒ cot A = \(\frac{8}{15}\)
\(\frac{\mathrm{B}}{\mathrm{P}}=\frac{8}{15}\)
B = 8k and P = 15 k
In right angled ΔABC, H² = B² + P² (By Pythagoras theorem)
= (8k)² + (15k)²
= 64k² + 225k²
= 289k²
∴ H = 17k (∵ Side cannot be -ve)
Now, sin A = \(\frac{\mathrm{P}}{\mathrm{H}}=\frac{15 \mathrm{k}}{17 \mathrm{k}}=\frac{15}{17}\)
sec A = \(\frac{\mathrm{H}}{\mathrm{B}}=\frac{17 \mathrm{k}}{8 \mathrm{k}}=\frac{17}{8}\)
Question 5.
Given sec θ = \(\frac{13}{12}\), calculate all other trigonometric ratios.
Solution :
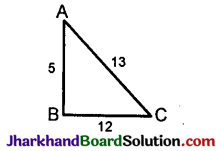
sec θ = \(\frac{1}{cos θ}\)
sec θ . cos θ = 1
\(\frac{13}{12} \times \frac{12}{13}\) = 1
AB² = AC² – BC²
= 13² – 12²
= 169 – 144
= 25
AB = \(\sqrt{25}\) = 5

![]()
Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution :
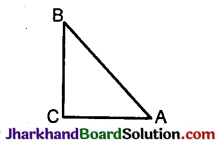
cos A = \(\frac{AC}{AB}\)
cos B = \(\frac{BC}{AB}\)
cos A = cos B
\(\frac{AC}{AB}=\frac{BC}{AB}\)
∴ AC = BC
∴ \(\hat{A}\) = \(\hat{B}\) (∵ Angles opposite to equal sides are also equal)
Question 7.
If cot θ = \(\frac{7}{8}\), evaluate: (i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\) (ii) cot² θ
Solution :
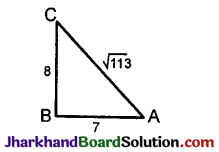
AC² = AB² + BC²
= 7² + 8²
= 49 + 64 = 113
AC = \(\sqrt{113}\)
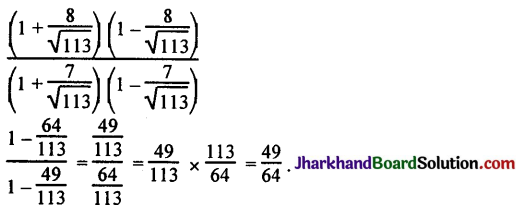
(ii) cot² θ = (cot θ)²
= (\(\frac{7}{8}\))² = \(\frac{49}{64}\)
Given cot θ = \(\frac{7}{8}\)
![]()
Question 8.
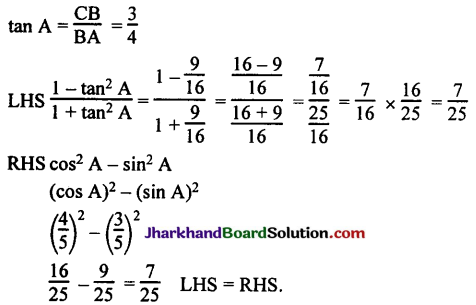
If 3 cot A = 4, check whether \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) = cos² A – sin² A or not.
Solution :
3 cot A = 4
cot A = \(\frac{4}{3}\)
AC² = AB² + BC²
= 4² + 3²
= 16 + 9
= 25
AC = \(\sqrt{25}\) = 5
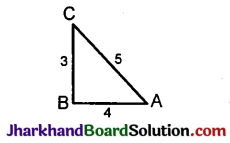
Question 9.
In triangle ABC, right-angled at B, if tan A = find the value of :
(i) sin A cos C + cos A sin C,
(ii) cos A cos C – sin A sin C.
Solution :
(i) sin A cos C + cos A sin C
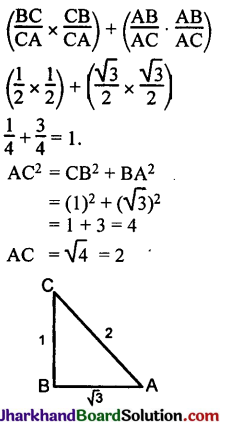
(ii) cos A . cos C – sin A . sin C
\(\frac{AB}{AC} \cdot \frac{BC}{AC}\) – \(\frac{BC}{AC} \cdot \frac{AB}{AC}\)
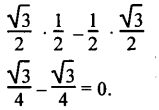
Question 10.
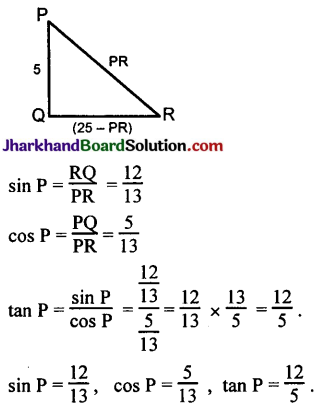
In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:
PR + QR = 25
QR = 25 – PR
PQ² + QR² = PR²
(5)² + (25 – PR)² = PR²
25 + (625 – 50PR + PR²) = PR²
650 – 50PR = PR² – PR² = 0
– 50PR = – 650
PR = \(\frac{-650}{-50}\) = 13.
PR = 13, QR = 25 – PR = 25 – 13 = 12, PQ = 5.
![]()
Question 11.
State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = \(\frac{12}{5}\) for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = \(\frac{4}{3}\) for some angle θ.
Solution :
(i) False, because the value of tan A increases from 0 to ∞. Also, tan 45° = 1.
(ii) True, because the value of sec A increases from 1 to ∞.
(iii) False, cos A is the abbreviation used for the cosine of angle A.
(iv) False, because cot A is one symbol. We cannot separate cot and A.
(v) False, because the value of sin θ always lies between 0 and 1. Here, sin θ = \(\frac{4}{3}\) which is greater than 1. So, it is not possible.