Jharkhand Board JAC Class 9 Maths Solutions Chapter 10 Circles Ex 10.3 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 10 Circles Ex 10.3
Page-176
Question 1.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Answer:
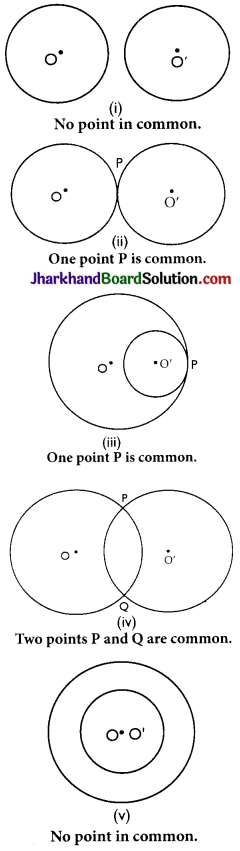
So, maximum number of common points = 2
Question 2.
Suppose you are given a circle. Give a construction to find its centre.
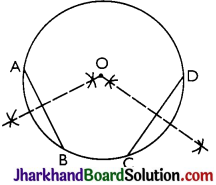
Answer:
Steps of construction:
Step I: A circle is drawn.
Step II: Two chords AB and CD are drawn.
Step III: Perpendicular bisector of the chords AB and CD are drawn.
Step IV: Let these two perpendicular bisectors meet at a point. The point of intersection of these two perpendicular bisectors is the centre of the circle.
![]()
Question 3.
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
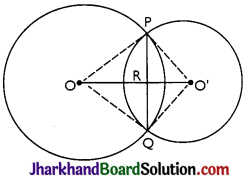
Answer:
Given: Two circles which intersect each other at P and Q.
To prove: 00′ is perpendicular bisector of PQ.
Proof: In ∆POO’ and ∆QOO’,
OP = OQ (Radii)
OO’ = 00′ (Common)
O’P = O’Q (Radii)
∆POO’ ≅ ∆QOO’
(SSS congruence criterion)
Thus,
∠POO’ = ∠QOO’ (CPCT) …(i)
In ∆POR and ∆QOR,
OP = OQ (Radii)
∠POR = ∠QOR (from i)
OR = OR (Common)
∴ ∆POR ≅ ∆QOR
(SAS congruence criterion)
Thus, PR = PQ (CPCT)
And, ∠PRO = ∠QRO (CPCT)
Also, ∠PRO + ∠QRO = 180° (Linear pair)
⇒ ∠PRO = ∠QRO = \(\frac{180°}{2}\) = 90°
Hence, OO’ is perpendicular bisector of PQ.