JAC Class 9 Maths Solutions Chapter 10 Circles Ex 10.4

Jharkhand Board JAC Class 9 Maths Solutions Chapter 10 Circles Ex 10.4 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 10 Circles Ex 10.4

Page-179

Question 1.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.

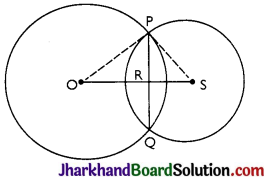
Answer:
OP = 5 cm, PS = 3 cm and OS = 4 cm.
We know that if two circles intersect at two points then their centres lie on the perpendicular bisector of the common chord.
So, OS is perpendicular bisector of PQ.
⇒ PQ = 2PR and ∠PRO = ∠PRS = 90°
Let RS be x ⇒ OR = 4 – x
In ∆POR,
OP² = OR² + PR²
⇒ 5² = (4 – x)² + PR²
⇒ 25 = 16 + x² – 8x + PR²
⇒ PR² = 9 – x² + 8x …(i)

In ∆PRS,
PS² – PR² + RS²
⇒ 3² = PR² + x²
⇒ PR² = 9 – x² …(ii)
Equating (i) and (ii),
9 – x² + 8x = 9 – x²
⇒ 8x = 0
⇒ x = 0
Putting the value of x in (i), we get
PR² – 9 – 0²
⇒ PR = 3 cm
Length of the Chord PQ = 2PR = 2 × 3 = 6 cm

Question 2.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.

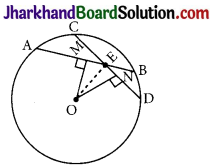
Answer:
Given: AB and CD are chords intersecting at E.
AB = CD
To prove: AE = DE and CE = BE
Construction: OM ⊥ AB and ON ⊥ CD. OE is joined.
Proof: OM bisects AB (OM ⊥ AB)
⇒ AM = MB = \(\frac{1}{2}\) AB
ON bisects Cp (ON ⊥ CD)
⇒ DN = CN = \(\frac{1}{2}\) CD
As AB = CD
thus, AM = ND …….(i)
and MB = CN ……..(ii)

In ∆OME and ∆ONE,
∠OME = ∠ONE = 90° (Perpendiculars)
OE = OE (Common)
OM = ON (AB = CD and thus equidistant from the centre)
∆OME ≅ ∆ONE by RHS congruence criterion.
ME = EN by CPCT …(iii)
Adding (i) and (ii), we get
AM + ME = ND + EN
⇒ AE = ED
Subtracting (iii) from (ii), we get
MB – ME = CN – EN
⇒ EB = CE

Question 3.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Answer:
Given: AB and CD are chords intersecting at E.
AB = CD, PQ is the diameter.
To prove: ∠BEQ = ∠CEQ

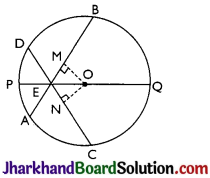
Construction: OM ⊥ AB and ON ⊥ CD. OE is joined.
In ∆OEM and ∆OEN,
OM = ON (AB = CD and Equal chords are equidistant from the centre)
OE = OE (Common)
∠OME = ∠ONE = 90° (Perpendiculars)
∆OEM = ∆OEN (by RHS congruence criterion)
Thus, ∠OME = ∠ONE (by CPCT)
⇒ ∠BEQ = ∠CEQ

Question 4.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see Fig).

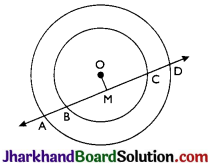
Answer:
OM ⊥ AD is drawn from O.
So, OM bisects AD (perpendicular from centre to the chord bisects the chord)
⇒ AM = MD …(i)
Also, OM bisects BC as OM ⊥ BC.
⇒ BM = MC …(ii)
Subtracting (ii) from (i), we get
AM – BM = MD – MC
⇒ AB = CD

Question 5.
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m e ach, what is the distance between Reshma and Mandip?
Answer:
Let A, B and C represent the positions of Reshma, Salma and Mandip respectively.
AB = 6 m and BC = 6 m Radius OA = 5 m
BM ⊥ AC is drawn.
ABC is an isosceles triangle as AB = BC, M is mid-point of AC. BM is perpendicular bisector of AC and thus it passes through the centre of the circle.

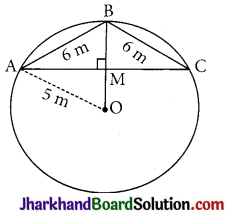
Let, AM = y and OM = x then BM = (5 – x).
Applying Pythagoras theorem in ∆OAM,
OA² = OM² + AM²
⇒ 5² = x² + y² …(i)
Applying Pythagoras theorem in ∆AMB,
AB²= BM² +AM²
⇒ 6² = (5-x)² + y² …(ii)
Subtracting (i) from (ii), we get
36 – 25 = (5 – x)² – x²
⇒ 11 = 25 – 10x
⇒ 10x = 14
⇒ x = \(\frac{7}{5}\)

Substituting the value of x in (i), we get
y² + \(\frac{49}{25}\) =25
⇒ y² = 25 – \(\frac{49}{25}\)
⇒ y² = \(\frac{625-49}{25}\)
⇒ y² = \(\frac{576}{25}\)
⇒ y = \(\frac{24}{5}\)

Thus,
AC = 2 × AM = 2 × y
= 2 × \(\frac{24}{5}\) m = \(\frac{48}{5}\) m = 9.6 m
Distance between Reshma and Mandip is 9.6 m.

Question 6.
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.

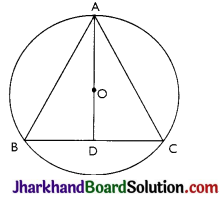
Answer:
Let A, B and C represent the positions of Ankur, Syed and David respectively. All three boys at equal distances thus, ABC is an equilateral triangle.
AD ⊥ BC is drawn.
Now, AD is median of ∆ABC and it passes through the centre O.
Also, O is the centroid of the ∆ABC.
OA is the radius of the triangle.
OA = \(\frac{2}{3}\) AD
Let the side of the triangle be a metres
then BD = \(\frac{a}{2}\) m.
Applying Pythagoras theorem in ∆ABD,
AB² = BD² + AD²
⇒ AD² = AB² – BD²
⇒ AD² = a² – (\(\frac{a}{2}\))²
⇒ AD² = \(\frac{3 a^2}{4}\)
⇒ AD = \(\frac{\sqrt{3} a}{2}\)
OA = \(\frac{2}{3}\) AD
⇒ 20m = \(\frac{2}{3}\) × \(\frac{\sqrt{3} a}{2}\)
⇒ a = \(20 \sqrt{3} \)m
∴ Length of the string is \(20 \sqrt{3} \)m