JAC Class 9 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.4

Jharkhand Board JAC Class 9 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.4 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.4

Page-225

Question 1.
Find the surface area of a sphere of radius:
(i) 10.5 cm
(ii) 5.6 cm
(iii) 14 cm
Answer:
(i) Radius of the sphere (r) = 10.5 cm
Surface area
= 4πr² = (4 × \(\frac{22}{7}\) × 10.5 × 10.5) cm²
= 1386 cm²

(ii) Radius of the sphere (r) = 5.6 cm
Surface area
= 4πr² = (4 × \(\frac{22}{7}\) × 5.6 × 5.6) cm²
= 394.24 cm²

(iii) Radius of the sphere (r) = 14 cm
Surface area
= 4πr² = (4 × \(\frac{22}{7}\) × 14 × 14) cm²
= 2464 cm²

Question 2.
Find the surface area of a sphere of diameter:
(i) 14 cm
(ii) 21cm
(iii) 3.5 m
Answer:
(i) Radius of a sphere (r) = \(\frac{14}{2}\) = 7 cm
Surface area = 4πr²
= (4 × \(\frac{22}{7}\) × 7 × 7) cm²
= 616 cm²

(ii) Radius of a sphere (r) = \(\frac{21}{2}\) = 10.5 cm
Surface area = 4πr²
= (4 × \(\frac{22}{7}\) × 10.5 × 10.5) cm²
= 1386 m²

(iii) Radius of a sphere (r) = \(\frac{3.5}{2}\) = 1.75 m
Surface area = 4πr²
= (4 × \(\frac{22}{7}\) × 1.75 × 1.75) cm²
= 38.5 m²

Question 3.
Find the total surface area of a hemisphere of radius 10 cm. (Use π = 3.14)
Answer:
r = 10 cm
∴ Total surface area of a hemisphere= 3πr²
= 3 × 3.14 × 10 × 10
= 942 cm²

Question 4.
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Answer:
Let r be the initial radius and R be the increased radius of balloon.
r = 7 cm and R = 14 cm
Ratio of the surface area
= \(\frac{4 \pi r^2}{4 \pi \mathrm{R}^2}\) = \(\frac{r^{2}}{R^{2}}\) =
Thus, the ratio of surface areas = 1 : 4.

Question 5.
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per 100 cm2.

Ans. Radius of the bowl (r) =\(\frac{10.5}{2}\) = 5.25 cm

Curved surface area of the hemispherical bowl = 2πr²
= (2 × \(\frac{22}{7}\) × 5.25 × 5.25) cm²
= 173.25 cm²

Rate of tin-plating is ₹ 16 per 100 cm²
Therefor, cost of 1 cm² = ₹ \(\frac{16}{100}\)
Total cost of tin-plating the hemisphere bowl
= 173.25 × \(\frac{16}{100}\) = ₹ 121.72

Question 6.
Find the radius of a sphere whose surface area is 154 cm².
Answer:
Let r be the radius of the sphere.
Surface area =154 cm²
⇒ 4πr² = 154
⇒ 4 × \(\frac{22}{7}\) × r² = 154
⇒ r² = \(\frac{154}{\left(4 \times \frac{22}{7}\right)}\)
⇒ r² = \(\frac{49}{4}\)
⇒ r = \(\frac{7}{2}\) = 3.5 cm

Question 7.
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
Answer:
Let the diameter of earth be r then the diameter of the moon = r/4
Radius of the earth = \(\frac{r}{2}\)
Radius of the moon = \(\frac{r}{8}\)
Ratio of their surface areas = \(\frac{4 \pi\left(\frac{r}{8}\right)^2}{4 \pi\left(\frac{r}{2}\right)^2}\)
= \(\frac{\left(\frac{1}{64}\right)}{\left(\frac{1}{4}\right)}\)
= \(\frac{4}{64}\) = \(\frac{1}{16}\)

Thus, the ratio of their surface areas is 1:16.

Question 8.
A hemispherical bowl is made of steel, 0. 25 cm thick. The inner radius of the . bowl is 5 cm. Find the outer curved surface area of the bowl.
Answer:
Inner radius of the bowl (r) = 5 cm
Thickness of the steel = 0.25 cm
∴ Outer radius (R)
= (r + 0.25) cm
= (5 + 0.25) cm
= 5.25 cm

Outer curved surface area = 2πR²
= 2 × \(\frac{22}{7}\) × 5.25 × 5.25
= 173.25 cm²

Question 9.
A right circular cylinder just encloses a sphere of radius r (see Fig.). Find
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in (i) and (ii)

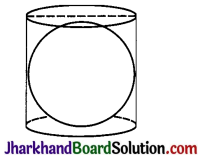
Answer:
(i) The surface area of the sphere with radius r = 4πr²
(ii) The right circular cylinder just encloses a sphere of radius r.
∴ The radius of the cylinder = r and its height = 2r
∴ Curved surface of cylinder = 2πrh = 2π × r × 2r = 4πr²

(iii) Ratio of the areas = 4πr² : 4πr² = 1 : 1.