JAC Class 9 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.6

Jharkhand Board JAC Class 9 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.6 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.6

Page-230

Question 1.
The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1000 cm³ = 1 L)
[Assume, π = \(\frac{22}{7}\)]
Answer:
Let the radius of the cylindrical vessel be r.
Height (h) of vessel = 25 cm
Circumference of vessel =132 cm
2πr = 132 cm
r = \(\frac{132 × 7}{2 × 22}\) cm = 21 cm

Volume of cylindrical vessel = πr²h = × (21)² × 25 cm³ = 34650 cm³
= \(\frac{34650}{1000}\) liters = 34.65 litres
[∵ 1 litre = 1000 cm³]
Therefore, such vessel can hold 34.65 litres of water.

Question 2.
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
Assume, n= \(\frac{22}{7}\)
Answer:
Inner radius (r ) of cylindrical pipe
= \(\frac{24}{2}\) cm = 12 cm

Outer radius (r2) of cylindrical pipe = \(\frac{28}{2}\) cm = 14 cm
Height (h) of pipe = Length of pipe = 35 cm

Volume of pipe = π\(\left(r_1^2-r_2^2\right)\)h
= [\(\frac{22}{7}\) × (14² – 12²) × 35] cm³
= 110 × 52 cm³ = 5720 cm³
Mass of 1 cm3 wood = 0.6 g
Mass of 5720 cm3 wood = (5720 × 0.6) g
= 3432 g = 3.432 kg

Question 3.
A soft drink is available in two packs:
(i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and
(ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
Assume, π = \(\frac{22}{7}\)
Answer:
(i) The tin can will be cuboidal in shape while the plastic cylinder will be cylindrical in shape.

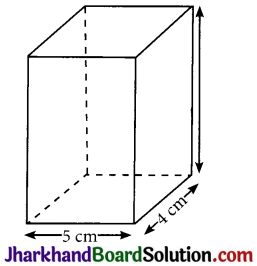
Length (l) of tin can = 5 cm
Breadth (b) of tin can = 4 cm
Height (h) of tin can = 15 cm
Capacity of tin can = l × b × h = (5 × 4 × 15) cm³ = 300 cm³

(ii)

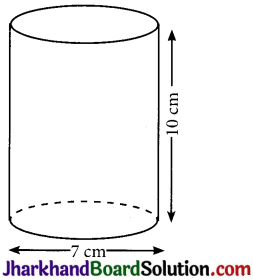
Radius (r) of circular end of plastic cylinder = \(\frac{7}{2}\) cm = 3.5 cm
Height (H) of plastic cylinder = 10 cm
Capacity of plastic cylinder = πr²H
= \(\frac{22}{7}\) × (3.5)² × 10 cm³
= 11 × 35 cm³ = 385 cm³

Therefore, plastic cylinder has the greater capacity.
Difference in capacities = (385 – 300) cm³ = 85 cm³

Question 4.
If the lateral surface of a cylinder is 94.2 cm² and its height is 5 cm, then find
(i) radius of its base
(ii) its volume.
[Use π= 3.14]
Answer:
(i) Height (h) of cylinder = 5 cm
Let radius of cylinder be r.

CSA of cylinder = 94.2 cm²
2πrh = 94.2 cm²
(2 × 3.14 × r × 5) cm = 94.2 cm²
r = 3 cm

(ii) Volume of cylinder = πr²h
= (3.14 x (3)2 x 5) cm³ = 141.3 cm³

Page-231

Question 5.
It costs ₹ 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of ₹ 20 per m², find:
(i) Inner curved surface area of the vessel
(ii) Radius of the base
(iii) Capacity of the vessel
Assume π = \(\frac{22}{7}\)
Answer:
(i) ₹ 20 is the cost of painting 1 m² area.
₹ 2200 is the cost of painting (\(\frac{1}{20}\) × 20) m² area = 110 m² area
Therefore, the inner surface area of the vessel is 110 m².

(ii) Let the radius of the base of the vessel be r.
Height (h)of the vessel = 10 m
Surface area = 2πrh = 110 m².
⇒ (2 × \(\frac{22}{7}\) × r × 10) = 110 m²
⇒ r = \(\frac{7}{4}\) m = 1.75 m

(iii) Volume of vessel = πr²h
= [\(\frac{22}{7}\) × (1.75)² × 10] m³
= 96.25 m³

Therefore, the capacity of the vessel is 96.25 m3 or 96250 litres.

Question 6.
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
Assume, π = \(\frac{22}{7}\)

Answer:
Let the radius of the cylindrical vessel be r.
Height (h) of cylindrical vessel = 1 m
Volume of cylindrical vessel = 15.4 litres = 0.0154 m³
πr²h = 0.0154
\(\frac{22}{7}\) × r² × 1 m = 0.0154³
⇒ r = 0.07 m

Total surface area of vessel = 2πr(r + h)
= [2 × \(\frac{22}{7}\) × 0.07(0.07 + 1)] m²
= 0.44 ×1.07 m²
= 0.4708 m²
Therefore 0.4708 m² of the metal sheet would be required to make the cylindrical vessel.

Question 7.
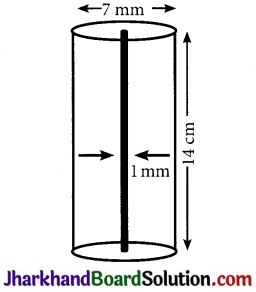
A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
Assume, π = \(\frac{22}{7}\)
Answer:
Radius (r) of pencil = \(\frac{7}{2}\) mm = \(\frac{0.7}{2}\) cm = 0.35 cm
Radius (r ) of graphite = \(\frac{1}{2}\) mm = \(\frac{0.1}{2}\) cm = 0.05 cm

Height (h) of pencil =14 cm
Volume of wood in pencil = π\(\left(r_1^2-r_2^2\right)\)h
= [\(\frac{22}{7}\) {(0.35)² – (0.05)²} × 14] cm³
= [\(\frac{22}{7}\) (0.1225 – 0.0025) × 14] m³
= 44 × 0.12 cm³ = 5.28 cm³

Volume of graphite
= π\({r_{1}^{2}}\)h
= \(\frac{22}{7}\) × (0.05)² × 14] cm³
= 44 × 0.0025 cm³ = 0.11 cm³

Question 8.
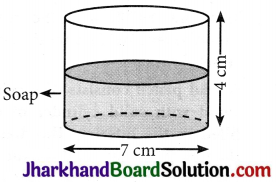
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Assume, π = \(\frac{22}{7}\)

Answer:
Radius (r) of cylindrical bowl = \(\frac{7}{2}\) cm = 3.5 cm
Height (h) of bowl, up to which bowl is filled with soup = 4 cm
Volume of soup in 1 bowl = πr²h
= [\(\frac{22}{7}\) × (3.5)² × 4] cm³
= (11 × 3.5 × 4) cm³= 154 cm³
Volume of soup given to 250 patients = (250 × 154) cm³ = 38500 cm³ = 38.5 litres.