Jharkhand Board JAC Class 9 Maths Important Questions Chapter 11 Constructions Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 11 Constructions
Question 1.
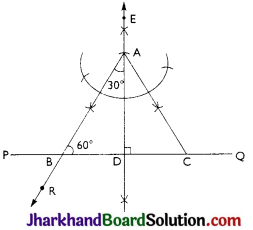
Construct an equilateral triangle if its altitude is 3.2 cm.
Solution :
Given: In an equilateral ΔABC, an altitude
AD = 3.2 cm
Required: To Construct an equilateral triangle ABC from the given data.
STEPS:
(i) Draw a line PQ
(ii) Construct a perpendicular bisector DE to PO.
(iii) Cut off DA = 3.2 cm from DE.
(iv) Construct ∠DAR = 30°.
The ray AR intersects PQ at B.
(v) Similarly, draw ∠DAC = 30.
The ray AC intersects PQ at C.
(vi) Join A with B and C.
We get the required ΔABC.
![]()
Question 2.
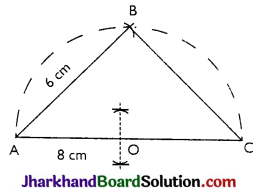
Construct a right-angled triangle whose hypotenuse measures 8 cm and one side is 6 cm.
Solution :
Given: Hypotenuse AC of a ΔABC = 8 cm and one side AB = 6 cm.
Required: To construct a right-angled ΔABC from the given data.
STEPS:
(i) Draw a line segment AC = 8 cm.
(ii) Mark the mid-point 0 of AC by doing perpendicular bisector of AC.
(iii) With O as centre and radius OA, draw a semicircle on AC.
(iv) With A as centre and radius equal to 6 cm, draw an arc, cutting the semicircle a B.
(v) Join A and B, B and C.
We get the required right-angled triangle ABC
Question 3.
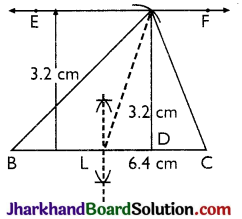
Construct a ΔABC in which BC = 6.4 cm, altitude from A is 3.2 cm and the median bisecting BC is 4 cm.
Solution :
Given: One side BC = 6.4 cm, altitude AD = 3.2 cm and the median AL = 4 cm.
Required: To construct a ΔABC form the given data
STEPS:
(i) Draw BC = 6.4 cm
(ii) Bisect BC at L.
(iii) Draw EF || BC at a distance 3.2 cm for BC
(iv) With L as centre and radius equal to 4 cm, draw an arc, cutting EF at A
(v) Join A and B ; A and C, A and L.
We get the required triangle ABC
![]()
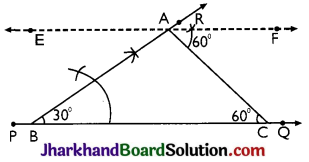
Question 4.
Construct a ΔABC in which ∠B = 30° and ∠C = 60° and the perpendicular from the vertex A to the base BC is 4.8 cm.
Solution :
Given: ∠B = 30°, ∠C = 60°, length of perpendicular from vertex A to be base BC = 4.8 cm.
Required: To construct a ΔABC from the given data.
STEPS :
(i) Draw any line PQ.
(ii) Take a point B on line PQ and construct ∠QBR = 30°
(iii) Draw a line EF || PQ at a distance of 4.8 cm from PQ, cutting BR at A.
(iv) Construct an angle ∠FAC = 60°, cutting PQ at C.
(v) Join A and C.
We get the required triangle ABC.
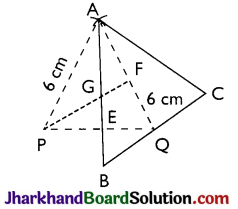
Question 5.
Construct a triangle ABC, the lengths of whose medians are 6 cm, 7 cm and 6 cm.
Solution :
Given: Median AD = 6 cm, median BE = 7 cm, median CF = 6 cm.
Required: To construct a AABC from the given data.
STEPS:
(i) Construct a ΔAPQ with AP = 6 cm, PQ = 7 cm and AQ = 6 cm.
(ii) Draw the medians AE and PF of ΔAPQ intersecting each other at G.
(iii) Produce AE to B such that GE = EB
(iv) Join B and Q and produce it to C, such that BQ = QC
(v) Join A and C. We get the required triangle ABC.