Students should go through these JAC Class 9 Maths Notes Chapter 8 चतुर्भुज will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 8 चतुर्भुज
चतुर्भुज : किसी एक ही समतल में स्थित चार सरल रेखाओं से घिरी बन्द आकृति को चतुर्भुज कहते हैं।
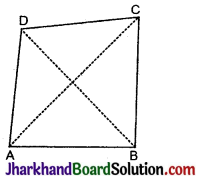
- किसी चतुर्भुज में चार भुजाएँ, चार शीर्ष तथा चार कोण होते है।
- चतुर्भुज के सम्मुख शीर्षों को मिलाने वाली रेखाखण्ड को विकर्ण कहते हैं। प्रत्येक चतुभुर्ज में दो विकर्ण होते हैं।
- चतुर्भुज के अन्तः कोणों का योग 4 समकोण या 360° होता है।
- किसी चतुर्भुज का परिमाप उसके विकर्णों के योग से अधिक होता है।
![]()
चतुर्भुज की सम्मुख भुजाएँ : चतुर्भुज की वे दो भुजाएँ, जिनका कोई उभयनिष्ठ बिन्दु न हो, सम्मुख भुजाएँ कहलाती हैं।
चतुर्भुज की क्रमागत भुजाएँ : चतुर्भुज की वे दो भुजाएँ, जिनका एक उभयनिष्ठ अंत्य बिन्दु (end-point) हो, क्रमागत भुजाएँ कहलाती हैं।
चतुर्भुज के सम्मुख कोण : चतुर्भुज के वे दो कोण. जिनको अन्तरित करने वाली भुजाओं में कोई भुजा उभयनिष्ठ न हो, सम्मुख कोण कहलाते हैं।
चतुर्भुज के क्रमागत कोण : चतुर्भुज के वे दो कोण, जिनको अंतरित करने वाली भुजाओं में से एक भुजा उभयनिष्ठ हो, क्रमागत कोण कहलाते हैं।
समलम्ब चतुर्भुज : यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म समान्तर हो, तो उस चतुर्भुज को समलम्ब चतुर्भुज कहते हैं।
समान्तर चतुर्भुज : यदि किसी चतुर्भुज की सम्मुख भुजाओं का प्रत्येक युग्म समान्तर हो, तो उसे समान्तर चतुर्भुज कहते हैं। इसे संक्षेप में ||gm से निरूपित करते हैं।
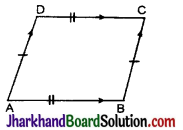
गुणधर्म :
(i) यदि समान्तर चतुर्भुज के दो सम्मुख शीर्षों को मिला दिया जाये, तो बना विकर्ण चतुर्भुज को दो सर्वांगसम त्रिभुजों में विभाजित करता है।
(ii) समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
(iii) समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।
(iv) समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
![]()
एक ऐसा समान्तर चतुर्भुज जिसकी सम्मुख भुजाएँ बराबर हों तथा प्रत्येक कोण समकोण हो, आयत (rectangle) कहलाती है।
एक ऐसा समान्तर चतुर्भुज जिसकी सम्मुख भुजाएँ लम्बाई में समान हों, समचतुर्भुज (rhombus) कहलाता है।
एक ऐसा समान्तर चतुर्भुज जिसकी चारों भुजाएँ बराबर हों और चारों कोण समकोण हो, उसे वर्ग (square) कहते हैं।
यदि एक समतल में दो रेखाएँ l व m ( समान्तर या प्रतिच्छेदी) दी हुयी हों और यदि एक तीसरी रेखा x उन्हें भिन्न बिन्दुओं P और O पर प्रतिच्छेदित करती हो, तो रेखाखण्ड PQ को दी गयी रेखाओं द्वारा इस रेखा (x) पर बनाया गया अन्तः खण्ड कहते हैं।