Students should go through these JAC Class 9 Maths Notes Chapter 10 वृत्त will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 10 वृत्त
→ वृत्त (Circle) : वृत्त एक समतल में स्थित उन बिन्दुओं का समुच्चय (Set) होता है, जो समतल में दिए गए एक स्थिर बिन्दु से दी हुई नियत दूरी पर होते हैं।
स्थिर बिन्दु को वृत्त का केन्द्र (Centre) और उस केन्द्र से वृत्त के प्रत्येक बिन्दु की नियत दूरी को वृत्त की त्रिज्या (Radius) कहते हैं।
(i) वृत्त की परिभाषा एक बिन्दुपध के रूप में भी दी जा सकती है।
परिभाषा : यदि एक समतल में कोई बिन्दु इस तरह गतिमान होता है कि समतल में दिए गए एक स्थिर बिन्दु से उसकी दूरी सदा ही नियत रही है, तो उस बिन्दु के पथ को वृत्त कहते हैं।
(ii) समुच्चय संकेतन में वृत्त को इस प्रकार लिखा जाता है:
C(O, r) = {X : OX = r}
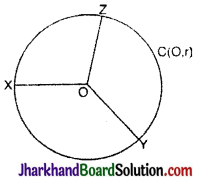
(iii) एक वृत्त की सभी त्रिज्याएँ समान होती हैं। आकृति में,
OX = OY = OZ = r
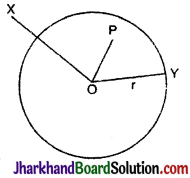
→ वृत्त का अन्तः और बाह्य भाग (Interior and Exterior of a Circle) :
बिन्दु को, जहाँ OP <r, वृत्त का अन्तः बिन्दु कहते हैं। वृत्त के अन्तःबिन्दु को I1 से प्रदर्शित करते हैं। बिन्दु Q को, जहाँ OQ > r वृत्त का बाह्य बिन्दु कहते हैं। वृत्त के बाह्य भाग को I2 से दशति हैं।
सांकेतिक रूप में,
I1 = {P: OP < r } तथा
I2 = {P: OP > r}
→ गोल चक्रिका (Circular Disc) वृत्त C (O, r) के अन्तःभाग और वत्त पर स्थित बिन्दुओं के समुच्चय को केन्द्र O तथा त्रिज्या r वाली एक गोल चक्रिका कहते हैं।
![]()
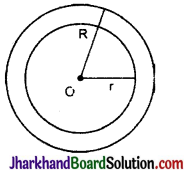
→ संकेन्द्रीय वृत्त (Concentric Circles): एक ही केन्द्र वाले दो या दो से अधिक वृत्तों को संकेन्द्रीय वृत्त कहते हैं।
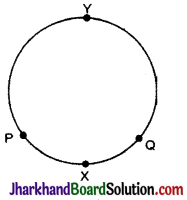
→ वृत्त का चाप (Arc of Circle) : यदि PQ वृत्त C (O, r) पर कोई दो बिन्दु हों तो वृत्त दो भागों में बँट जाता है, जिनमें से प्रत्येक भाग को वृत्त का चाप कहते हैं। छोटे भाग को लघु चाप (Minor arc) तथा बड़े भाग को दीर्घ चाप (Major arc) कहते हैं। चाप को प्रायः ![]() से प्रदर्शित करते हैं। आकृति में \(\overparen{P X Q}\) लघु चाप तथा \(\overparen{P Y Q}\) दीर्घ चाप है।
से प्रदर्शित करते हैं। आकृति में \(\overparen{P X Q}\) लघु चाप तथा \(\overparen{P Y Q}\) दीर्घ चाप है।
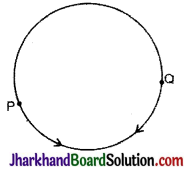
→ दक्षिणावर्त दिशा और वामावर्त दिशा (Clockwise Direction and Counter Clockwise or Anticlockwise Direction) : जिस दिशा में घड़ी की मिनट वाली सुई घूमती है, उसे दक्षिणावर्त दिशा तथा उसकी उलटी दिशा को वामावर्त दिशा कहते हैं। आकृति में P से Q की ओर की दिशा वामावर्त दिशा तथा Q से P की ओर की दिशा दक्षिणावर्त दिशा है।
→ वृत्त की जीवा (Chord of a Circle): वृत्त के दो बिन्दुओं को मिलाने वाले रेखाखण्ड को वृत्त की जीवा कहते हैं। आकृति में वृत्त पर स्थित प्रदत्त दो बिन्दुओं P तथा Q से खींची गयी रेखा जीवा PQ है।
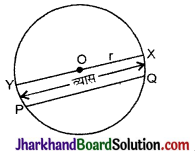
→ वृत्त का व्यास (Diameter of a Circle) : वृत्त के केन्द्र से होकर जाने वाली जीवा को वृत्त का व्यास कहते हैं। आकृति में XY वृत्त का व्यास है। यदि वृत्त C (O, r) का व्यास हो, तो
d = 2r.
नोट:
- एक वृत्त के अनेक व्यास होते हैं।
- वृत्त के समस्त व्यास लम्बाई में समान होते हैं।
- वृत्त का व्यास उस वृत्त की सबसे बड़ी जीवा होती है।
- वृत्त का व्यास वृत्त की त्रिज्या का दोगुना होता है।
![]()
→ अर्द्धवृत्त (Semicircle) : व्यास वृत्त को दो बराबर चापों में विभाजित करता है। प्रत्येक चाप अर्द्धवृत्त कहलाता है।
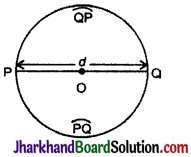
आकृति में \(\overparen{P Q}\) तथा \(\overparen{Q P}\) अर्द्धवृत्त हैं।
→ वृत्तखण्ड (Segment) वृत्त की जीवा वृत्ताकार चक्रिका को दो भागों में विभक्त करती है उन दो भागों में से प्रत्येक भाग को वृत्तखण्ड कहते हैं। छोटे भाग को लघु वृत्तखण्ड (Minor segment) और बड़े भाग को दीर्घ वृत्तखण्ड (Major segment) कहते हैं।

इन खण्डों में से प्रत्येक खण्ड को दूसरे खण्ड का एकान्तर वृत्तखण्ड (Alternate segment) कहते हैं।
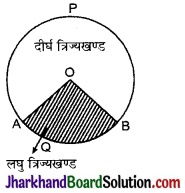
→ त्रिज्यखण्ड (Sector) किसी वृत्त के चाप तथा उसके अन्त्यबिन्दु से जाने वाली त्रिज्याओं से बनी आकृति त्रिज्यखण्ड कहलाती है। आकृति में OAQB लघु त्रिज्यखण्ड (Minor Sector) तथा OAPB दीर्घ त्रिज्यखण्ड (Major Sector) है।
→ चाप का अंशमाप (Degree Measure of an Arc) मान लीजिए C(O, r) एक वृत्त है, तो उस कोण को जिसका शीर्ष O है, वृत्त का केन्द्रीय कोण (Central angle) कहा जाता है। वृत्त की अंश माप 365° तथा अर्द्धवृत्त की अंशमाप 180° होती है चाप की अंश माप को M \(\overparen{A B}\) से प्रकट करते हैं। यदि चाप द्वारा केन्द्र पर अन्तरित कोण अंशों में दिया हों अथवा अंशों में ज्ञात किया जाए तो वह कोण चाप का अंशमाप कहलाता है।
अतः m\(\overparen{A B}\) = ∠AOB का मान अंशों में।
→ सर्वांगसम वृत्त (Congruent Circles) ऐसे दो या दो से अधिक वृत्त सर्वांगसम वृत्त कहलाते हैं, जिनकी त्रिज्याओं की माप समान हों। आकृति में, OA = O’C।
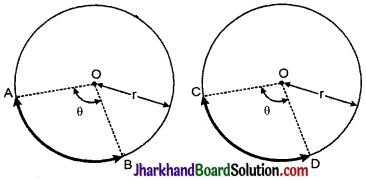
→ सर्वांगसम चाप (Congruent Arcs) : दो सर्वांगसम वृत्तों के ऐसे चाप जिनके अंशमाप समान हों, सर्वागसम चाप कहलाते हैं। आकृति में चाप AB, चाप CD के सर्वागसम है इसे “\(\overparen{A B}\) ≡ \(\overparen{C D}\)” भी लिखा जा सकता है।
![]()
→ वृत्त की परिधि (Circumference of a Circle) : वृत्त के परिमाप को परिधि कहते हैं।
यदि त्रिज्या r होता
परिधि = 2πr ⇒ πd
यहाँ π = \(\frac{22}{7}\) या 3.1416.
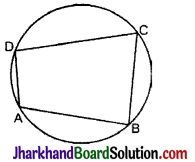
→ चक्रीय चतुर्भुज (Cyclic Quadrilateral) : किसी चतुर्भज को चक्रीय चतुर्भुज कहते हैं, यदि उसके चारों शीर्ष बिन्दु वृत्त पर स्थित हों। आकृति में ABCD चक्रीय चतुर्भुज है।