Students should go through these JAC Class 9 Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल और आयतन will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल और आयतन
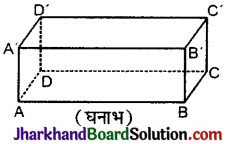
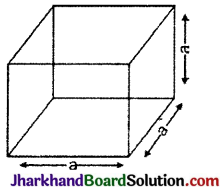
→ घनाभ : यदि समान्तर षट्फलक का प्रत्येक फलक आयत हो, तो उसे घनाभ कहते हैं। घनाभ को आयत फलकी ठोस भी कहते हैं।
जैसे ईंट, सन्दूक, कमरा आदि।
घनाभ के 6 पृष्ठ (फलक) 8 शीर्ष एवं 12 कोरें होती हैं।
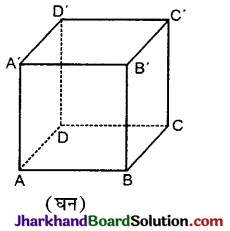
→ घन : यदि घनाभ का प्रत्येक फलक वर्गाकार हो, तो उसे घन कहते हैं अर्थात् घन की लम्बाई, चौड़ाई और ऊँचाई बराबर होती है।
द्विविमीय : समतल में स्थित प्रत्येक आकृति द्विविमीय (Two Dimensional) कहलाती हैं क्योंकि उनमें केवल दो विमाएँ (लम्बाई तथा चौड़ाई) होती है।
त्रिविमीय : दैनिक जीवन में प्रयोग की जाने वाली समस्त वस्तुएँ त्रिविमीय (Three Dimensional) होती हैं। इनमें लम्बाई चौड़ाई के साथ-साथ ऊँचाई भी होती हैं। द्विविमीय वस्तुओं द्वारा केवल समतल में स्थान घेरा जाता है, किन्तु त्रिमीय वस्तुओं में ऊँचाई होने के कारण, समतल से ऊपर भी स्थान घेरा जाता है।
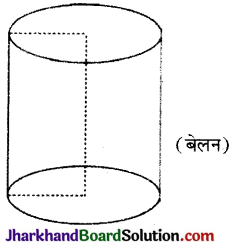
→ बेलन : बेलन एक ऐसी त्रिविमीय ठोस आकृति होती है, जो दो वृत्त तथा एक वक्र आयत से मिलकर बनी होती है। इसके दो सिरे समान त्रिज्या वाले वृत्त होते हैं एवं पार्श्व पृष्ठ वक्र (curved) होता है।
![]()
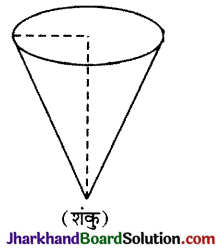
→ शंकु : एक त्रिविमीय संरचना है, जो शीर्ष बिन्दु और एक आधार (आश्वयक नहीं कि यह वृत्त ही हो) को मिलाने वाली रेखाओं द्वारा निर्मित होती है। यदि किसी शंकु का आधार एक वृत्त हो तो उसे लम्ब वृत्तीय शंकु कहते हैं।
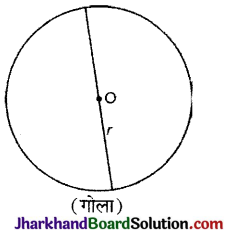
→ गोला : किसी वृत्त को उसके व्यास के अनुदिश घुमाने से प्राप्त ठोस आकृति को गोला कहते हैं। वृत्त का व्यास, त्रिज्या और केन्द्र ही प्राप्त गोले के क्रमशः व्यास, त्रिज्या और केन्द्र होते हैं।
→ अर्द्धगोला : किसी भी गोले को यदि उसके व्यास से काटकर दो भागों में विभक्त कर दिया जाए तो प्राप्त दोनों भाग समान आयतन और पृष्ठीय क्षेत्रफल के अर्द्धगोला कहलाते हैं।

महत्वपूर्ण सूत्र :
→ घनाभ : यदि किसी घनाभ की लम्बाई = l, चौड़ाई = b तथा ऊँचाई = h हो तो
घनाभ का पृष्ठीय क्षेत्रफल = 2 (ल × चौ + चौ × ॐ + ॐ × ल)
(S.A) = 2(lb + bh + hl) वर्ग इकाई
आयतन = ल. × चौ. × ॐ.
v = lbh घन इकाई
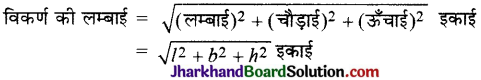
![]()
→ घन : यदि किसी घन की प्रत्येक भुजा की लम्बाई a इकाई हो तो-
घन का पृष्ठीय क्षेत्रफल = 6 (भुजा)2 वर्ग इकाई
S.A. = 6a2
आयतन = भुजा × भुजा × भुजा
[V = a × a × a = a3 घन इकाई]
विकर्ण = भुजा × \(\sqrt{3}\) इकाई
D = \(\sqrt{3}\)a इकाई
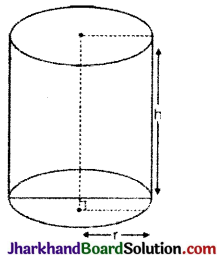
→ बेलन : यदि बेलन की त्रिज्या = r तथा ऊँचाई = h हो तो,
वक्र पृष्ठीय क्षेत्रफल = 2 × π × त्रिज्या × ऊँचाई
C.S.A. = 2πrh वर्ग इकाई
आयतन = π × त्रिज्या × त्रिज्या × ऊँचाई
V = πr2h घन इकाई
सम्पूर्ण पृष्ठ = 2π × त्रिज्या (ऊँचाई + त्रिज्या)
T.S.A. = 2πr (h + r) वर्ग इकाई
बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल = पृष्ठीय क्षेत्रफल + दोनों आधारों का क्षेत्रफल
= 2πrh + 2πr2
= 2πr (h + r) वर्ग इकाई
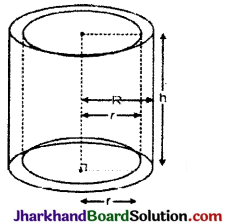
→ खोखले बेलन : यदि खोखले बेलन की बाह्य त्रिज्या = R
तथा आन्तरिक त्रिज्या = r एवं ऊँचाई = है तो,
आयतन = π(बाह्य त्रिज्या2 – आन्तरिक त्रिज्या2)h
= π(R2 – r2) h
= π(R + r) (R – r)h घन इकाई.
→ लम्ब वृत्तीय शंकु :
यदि त्रिज्या = r, ऊँचाई = h तथा प्रियंक ऊँचाई = l हो तो
लम्ब वृत्तीय शंकु का वक्रपृष्ठ = π × त्रिज्या × त्रियक ऊँचाई
S.A. = πrl वर्ग इकाई
आयतन = \(\frac{1}{3}\) × π × त्रिज्या × त्रिज्या × ऊँचाई
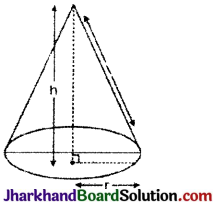
V = \(\frac{1}{3}\)πr2h घन इकाई
सम्पूर्ण पृष्ठ = π × त्रिज्या (त्रिर्यक ऊँचाई + त्रिज्या)
T.S.A. = πr (l + r) वर्ग इकाई

![]()
→ गोला :
गोले का पृष्ठीय क्षेत्रफल = 4πr2 वर्ग इकाई
गोले का आयतन = \(\frac{4}{3}\)πr3 घन इकाई
अर्द्धगोले का वक्रपृष्ठ = 2πr2 वर्ग इकाई
⇒ अर्द्धगोले का सम्पूर्ण पृष्ठ = 2πr2 + πr2
= 3πr2 वर्ग इकाई
अर्द्धगोले का आयतन = \(\frac{2}{3}\)πr3 घन इकाई