JAC Class 9 Maths Notes Chapter 14 सांख्यिकी

Students should go through these JAC Class 9 Maths Notes Chapter 14 सांख्यिकी will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 9 Maths Notes Chapter 14 सांख्यिकी

→ “सांख्यिकी एक ऐसा विज्ञान है, जिसका सम्बन्ध, संख्यात्मक आँकड़ों के संग्रह, उनके प्रस्तुतीकरण और उनसे निष्कर्ष निकालने की प्रक्रिया से हैं।”

→ “सांख्यिकीय आँकड़ों से अभिप्राय उन संख्यात्मक तथ्यों अथवा प्रेक्षणों है, जिनका संग्रह किसी पूर्व निर्धारित उद्देश्य के लिए किया जाता है।”
(i) प्राथमिक आँकड़े (Primary Data) : वे आँकड़े जो अन्वेषक द्वारा अपने उद्देश्य की पूर्ति हेतु स्वयं प्रथम बार एकत्रित किए जाते हैं, प्राथमिक आँकड़ें कहलाते हैं।
(ii) द्वितीयक आँकड़े (Secondary Data) : वे आँकड़े जो मूल रूप से किसी अन्य व्यक्ति द्वारा किसी और उद्देश्य से एकत्रित किए जाते हैं, किन्तु अपने विश्लेषण के लिए अन्वेषक द्वारा प्रयुक्त होते हैं, द्वितीयक आँकड़े अथवा गौण आँकड़े कहलाते हैं।

→ “ऐसा समूह जिसमें आँकड़ों को विभिन्न श्रेणियों में विभक्त किया जाता है। वर्ग कहलाता है।” उदाहरणार्थ 10 – 20, 20 – 30 अथवा 0 – 5, 5 – 10 आदि ।

→ “किसी भी वर्ग के प्रथमांक अथवा न्यूनतम राशि को सम्बन्धित वर्ग की निम्न सीमा कहते हैं।”
उदाहरणार्थ : 10 – 20 वर्ग में निम्न सीमा = 10
20 – 30 वर्ग में निम्न सीमा = 20

→ “किसी भी वर्ग के अंतिमांक अथवा उच्चतम राशि को उस वर्ग की उच्च सीमा कहते हैं।”
उदाहरणार्थ : 10 – 20 वर्ग में उच्च सीमा = 20
20 – 30 वर्ग में उच्च सीमा = 30

→ “किसी भी वर्ग की उच्च एवं निम्न सीमा के अन्तर को उस वर्ग का वर्ग अन्तराल कहते हैं।”
वर्ग अन्तराल = वर्ग की उच्च सीमा – वर्ग की निम्न सीमा

→ “किसी भी वर्ग की उच्च सीमा एवं निम्न सीमा के मध्य मूल्य को उस वर्ग का वर्ग चिह्न अथवा मध्य बिन्दु कहते हैं।”

→ “दिए गए आँकड़ों में आने वाले प्रत्येक आँकड़ो की कुल संख्या को उस आँकड़े की बारम्बारता कहते हैं।”

→ “किसी वर्ग विशेष की सीमा में आने वाले आँकड़ों की कुल संख्या को उस वर्ग की आवृत्ति कहते हैं।”

→ “यदि वर्गीकृत आँकड़ों को, प्रत्येक आँकड़े की बारम्बारता के साथ सारणी के रूप में प्रस्तुत किया जाता है, तो इस प्रकार निर्मित सारणी को बारम्बारता सारणी कहते हैं।”

→ “यदि किसी वर्ग विशेष की बारम्बारता और उससे पूर्व के समस्त वर्गों की बारम्बारताओं का योग करें तो प्राप्त योगफल उस वर्ग की संचयी बारम्बारता कहलाता है।”

→ “वह सारणी जिससे प्रत्येक वर्ग की संचयी बारम्बारता प्रकट होती हो संचयी बारम्बारता सारणी कहलाती है।”

→ “कुल आँकड़ों की अधिकतम व न्यूनतम राशि के अन्तर को परिसर (Range) कहते हैं।”

→ “आँकड़ों के वर्गीकरण की मुख्यतः दो विधियाँ हैं :
(i) अपवर्जी विधि (Exclusive Method) : इस विधि में प्रत्येक वर्ग की उच्च सीमा, आगे वाले वर्ग अन्तराल की निम्न सीमा होती है।
उदाहरणार्थ: 0 – 10, 10 – 20, 20 – 30, 30 – 40 इस वर्गीकरण में किसी कक्षा के 0 से 40 प्राप्तांकों को अपवर्जी विधि द्वारा व्यक्त किया गया है।
(ii) समावेशी विधि (Inclusive Method) : इस विधि के अन्तर्गत किसी वर्ग की उच्च सीमा को अगले वर्ग की निम्न सीमा के रूप में समावेशित नहीं किया जाता है।
उदाहारणार्थ किसी कक्षा के विद्यार्थियों द्वारा 0 उसे 40 तक प्राप्ताकों की समावेशी विधि है।
0 – 9, 10 – 19, 20 – 29, 30 – 39.

→ “वर्गीकृत आँकड़ों को एक सुव्यवस्थित ढंग से पंक्तियों एवं स्तम्भों में लिखने के रूप को सारणीयन कहते हैं।”

→ “जब आँकड़ो को सरल, सुन्दर तथा बोधगम्य बनाने के लिए उन्हें चित्रों द्वारा निरूपित किया जाता है, तो उसे आँकड़ों का चित्रों द्वारा निरूपण कहते हैं। ये मुख्यत: तीन प्रकार के होते हैं:
(i) दण्ड आलेख (Bar Graph): इसके द्वारा एकल अथवा सामूहिक सांख्यिकीय आँकड़ों को आयताकार दण्डों द्वारा प्रदर्शित किया जाता है।” जहाँ प्रत्येक दण्ड की लम्बाई उसके द्वारा प्रदर्शित किए जा रहे मान के अनुपात में रखी जाती है।
(ii) आयत चित्र (Histogram) आयताकार चित्रों द्वारा आवृत्ति वितरण का एक ग्राफीय निरूपण जिसमें चौड़ाई की दिशा में वर्ग अन्तराल और लम्बाई की दिशा में सम्बन्धित आवृत्ति को प्रदर्शित किया जाता है।
(iii) बारम्बारता बहुभुज (Frequency Polygon): आयत चित्र के प्रत्येक आयत के ऊपर की भुजाओं के मध्य बिन्दुओं को मुक्त हस्त रेखा द्वारा मिला दिया जाता है फिर प्रथम और अन्तिम आयतों के ऊपर की भुजाओं के मध्य बिन्दुओं को क्रमश: प्रथम और अन्तिम वर्ग अन्तरालों के आधार पर मध्य बिन्दुओं से मिला दिया जाता है। इस प्रकार बने बारम्बारता बहुभुज का क्षेत्रफल आयत चित्र के क्षेत्रफल के बराबर होता है।

→ केन्द्रीय प्रवृत्ति के माप (Measures of Central Tendency) : “केन्द्रीय प्रवृत्ति उस माप को कहते हैं, जो दिए गए आँकड़ों का प्रतिनिधित्व करता है।” केन्द्रीय प्रवृत्ति के मापों से तात्पर्य औसत मान से होता है।”
(i) समान्तर माध्य (Mean): सांख्यिकीय आँकड़ों के औसत (Average) मान को समान्तर माध्य कहते हैं।
यदि दिए गए पद x₁, x₂, x₃, x₄, …….., x_n हैं तो

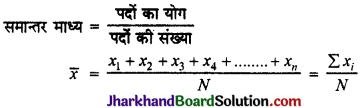
यदि आँकड़ों के साथ बारम्बारता भी दी गयी है तो
\(\bar{x}\) = \(\frac{\sum f_i x_i}{N}\)
(ii) माध्यिका (Median) : यदि दिए गए आँकड़े आरोही अथवा अवरोही क्रम में हैं तो
माध्यिका = \(\frac{N+1}{2}\)
यदि प्राप्त आँकड़ें सम संख्या हैं तो

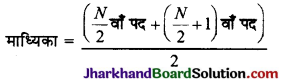
(iii) बहुलक (Mode) : किसी प्रेक्षण में सर्वाधिक आवृत्ति वाला वर्ग बहुलक वर्ग कहलाता है।