JAC Class 9 Maths Solutions Chapter 1 संख्या पद्धति Ex 1.2

Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 संख्या पद्धति Ex 1.2 Textbook Exercise Questions and Answers.

JAC Board Class 9 Maths Solutions Chapter 1 संख्या पद्धति Exercise 1.2

प्रश्न 1.
नीचे दिए गए कथन सत्य हैं या असत्य? कारण के साथ अपने उत्तर दीजिए।
(i) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।
(ii) संख्या रेखा का प्रत्येक बिन्दु \(\sqrt{m}\) के रूप का होता है, जहाँ m एक प्राकृत संख्या है।
(iii) प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या होती है।
हल:
(i) यह कथन सत्य है, वास्तविक संख्याओं के समुच्चय में समस्त परिमेय तथा अपरिमेय संख्याएँ सम्मिलित की जाती हैं। अतः प्रत्येक अपरिमेय संख्या वास्तविक संख्या होती है।

(ii) यह कथन असत्य है, क्योंकि संख्या रेखा पर सभी वास्तविक संख्याएँ निरूपित की जा सकती हैं। यहाँ m एक प्राकृत संख्या है जो यह इंगित करती है कि \(\sqrt{1}\), \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{4}\), \(\sqrt{5}\)…. बिन्दु ही संख्या-रेखा पर स्थित हैं उनसे अलग बिन्दु संख्या रेखा पर स्थित नहीं हो सकते। जबकि वास्तविकता यह है कि दी हुई किन्हीं दो क्रमिक संख्याओं को निरूपित करने वाले बिन्दुओं के मध्य विस्तृत अन्तराल होता है; जैसे: \(\sqrt{2}\) = 1.412… और \(\sqrt{3}\) = 1.732…. तब 1.412 और 1.732 के मध्य पड़ने वाली संख्याओं को भी संख्या-रेखा पर स्थान प्राप्त होता है। इसके अतिरिक्त ऋणात्मक संख्याएँ संख्या-रेखा पर स्थित होती हैं। अतः संख्या रेखा का प्रत्येक बिन्दु \(\sqrt{m}\) से व्यक्त नहीं किया जा सकता (जबकि m = एक प्राकृत संख्या हो)।

(iii) यह कथन असत्य है, क्योंकि परिमेय संख्याओं और अपरिमेय संख्या के संग्रह से वास्तविक संख्याओं के समुच्चय का निर्माण होता है अतः प्रत्येक अपरिमेय संख्या तो वास्तविक संख्या हो सकती है परन्तु प्रत्येक वास्तविक संख्या का अपरिमेय होना आवश्यक नहीं है जैसे : 2 एक वास्तविक संख्या है परन्तु यह अपरिमेय नहीं है।

प्रश्न 2.
क्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय होते हैं? यदि नहीं, तो एक ऐसी संख्या के वर्गमूल का उदाहरण दीजिए जो एक परिमेय संख्या है।
हल:
नहीं, सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय नहीं होते हैं।
उदाहरण : \(\sqrt{1}\) = ±1, \(\sqrt{4}\) = ±2, \(\sqrt{9}\) = ±3, इत्यादि परिमेय संख्याएँ हैं।

प्रश्न 3.
दिखाइए कि संख्या-रेखा पर \(\sqrt{5}\) को किस प्रकार निरूपित किया जा सकता है ?
हल:
(i) संख्या रेखा खींचकर OA = 2 इकाई ली।
(ii) OA के 4 बिन्दु पर OB = 1 इकाई लम्ब डाला।
(iii) O को B से मिलाया।
समकोण ΔOAB में पाइथागोरस प्रमेय से,
OB = \(\sqrt{O A^2+A B^2}\) = \(\sqrt{2^2+1^2}\) = \(\sqrt{5}\)

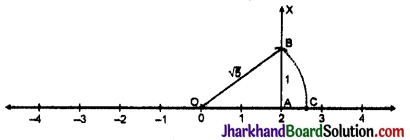
O को केन्द्र मानकर OB त्रिज्या का चाप खींचा जो संख्या रेखा को C बिन्दु पर काटता है।
OC = OB = \(\sqrt{5}\) = 2.236 (लगभग)
अतः \(\sqrt{5}\) को संख्या रेखा पर बिन्दु C के रूप में निरूपित किया जा सकता है।

प्रश्न 4.
कक्षा में वर्गमूल सर्पिल की रचना क्रियाकलाप द्वारा करिये।
हल:
कागज की एक बड़ी शीट लेकर सबसे पहले एक बिन्दु O लिया और एकक लम्बाई का रेखाखण्ड OP₁ खींचा। बिन्दु P₁ पर लम्ब रेखाखण्ड P₁P₂ एकक लम्बाई का खींचा। अब O और P₂ को मिलाया OP₂ रेखाखण्ड \(\sqrt{2}\) को दर्शाता है। इसी प्रकार बिन्दु P₂ पर एकक लम्बाई का रेखाखण्ड P₂P₃ खींचा, फिर P₃ को O से मिलाया जो \(\sqrt{3}\) को निरूपित करता है। इसी प्रकार P₃ पर एकक लम्बाई का लम्ब रेखाखण्ड P₃P₄ खींचा तथा P₄ को O से मिलाया जो कि \(\sqrt{4}\) को निरूपित करता है।

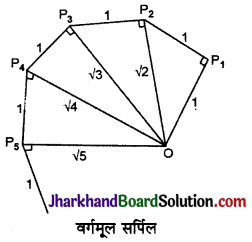
इसी प्रकार की पुनरावृत्ति के द्वारा \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{4}\), \(\sqrt{5}\), \(\sqrt{6}\)… दशांने वाला एक वर्गमूल सर्पिल प्राप्त किया जा सकता है।