Jharkhand Board JAC Class 9 Maths Solutions Chapter 3 निर्देशांक ज्यामिति Ex 3.1 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 3 निर्देशांक ज्यामिति Exercise 3.1
प्रश्न 1.
एक अन्य व्यक्ति को आप अपने अध्ययन मेज पर रखी टेबल लैंप की स्थिति किस तरह बताएँगे ?
हल:
माना कि मेज का तल एक समतल है और उस पर रखा हुआ टेबल- लैम्प समतल में स्थित एक बिन्दु है।
मेज की एक कोर के साथ इस प्रकार खड़े हुए कि इस कोर के साथ लगी दूसरी कोर बाएँ हाथ की ओर रहे।
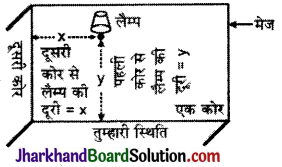
यदि दूसरी कोर से लैम्प की दूरी x यूनिट हो और पहली कोर से लैम्प की दूरी y यूनिट हो, तो लैम्प की स्थिति = (x, y).
![]()
प्रश्न 2.
(सड़क योजना): एक नगर में दो मुख्य सड़कें हैं, जो नगर के केन्द्र पर मिलती हैं। ये दो सड़कें उत्तर-दक्षिण की दिशा और पूर्व – पश्चिम की दिशा में हैं। नगर की अन्य सभी सड़कें इन मुख्य सड़कों के समान्तर परस्पर 200 मीटर की दूरी पर हैं। प्रत्येक दिशा में लगभग पाँच सड़कें हैं। 1 सेंटीमीटर = 200 मीटर का पैमाना लेकर अपनी नोट बुक में नगर का एक मॉडल बनाइए। सड़कों को एकल रेखाओं से निरूपित कीजिए।
आपके मॉडल में एक-दूसरे को काटती हुई अनेक क्रॉस-स्ट्रीट (चौराहे) हो सकती हैं। एक विशेष क्रॉस-स्ट्रीट दो सड़कों से बनी है, जिनमें से एक उत्तर-दक्षिण दिशा में जाती है और दूसरी पूर्व-पश्चिम दिशा में प्रत्येक क्रॉस-स्ट्रीट का निर्देशन इस प्रकार किया जाता है : यदि दूसरी सड़क उत्तर-दक्षिण दिशा में जाती है और पाँचवीं सड़क पूर्व-पश्चिम दिशा में जाती है और ये एक क्रॉसिंग पर मिलती हैं, तब इसे हम क्रॉस-स्ट्रीट (2, 5) कहेंगे। इसी परम्परा से यह ज्ञात कीजिए कि :
(i) कितनी क्रॉस-स्ट्रीटों को (4, 3) माना जा सकता है ?
(ii) कितनी क्रॉस-स्ट्रीटों को (3, 4) माना जा सकता है ?
हल:
मार्ग की योजना की आकृति निम्न प्रकार बना सकते हैं:
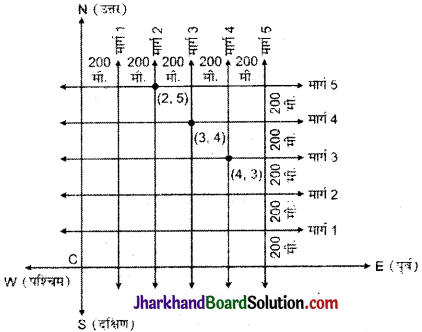
दोनों ही क्रॉस मार्ग आकृति में दिखाये गये हैं।
(i) (4, 3) का केवल एक क्रॉस मार्ग माना जा सकता है।
(ii) (3, 4) का केवल एक क्रॉस मार्ग माना जा सकता है।