Jharkhand Board JAC Class 9 Maths Solutions Chapter 7 त्रिभुज Ex 7.5 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 7 त्रिभुज Exercise 7.5
प्रश्न 1.
ABC एक त्रिभुज है। इसके अभ्यन्तर में एक ऐसा बिन्दु ज्ञात कीजिए, जो ΔABC के तीनों शीर्षो से समदूरस्थ है।
हल:
दिया है : ΔABC
ज्ञात करना है : बिन्दु P जो शीर्षों A, B तथा C से समदूरस्थ है।
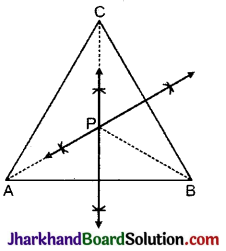
रचना : भुजाओं AB तथा BC के लम्ब समद्विभाजक खींचे जो एक दूसरे को प्रतिच्छेदित करते हैं।
बिन्दु P ही अभीष्ट बिन्दु है।
उपपत्ति: P को क्रमश A, B तथा C से मिलाने पर
PA = PB = PC इति सिद्धम्।
![]()
प्रश्न 2.
किसी त्रिभुज के अभ्यंतर में एक ऐसा बिन्दु ज्ञात कीजिए जो त्रिभुज की सभी भुजाओं से समदूरस्थ है।
हल:
दिया है : ΔABC
ज्ञात करना है: भुजाओं AB, BC तथा CA से समदूरस्थ बिन्दु O।
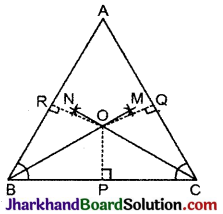
रचना : ΔABC के ∠B तथा ∠C के समद्विभाजक खींचे जो परस्पर O पर
प्रतिच्छेदित करते हैं।
O ही अभीष्ट बिन्दु है।
उपपत्ति: बिन्दु से भुजाओं AB, BC तथा CA पर
क्रमश: OR, OP तथा OQ लम्ब डाले।
नापने पर OR = OP = OQ इति सिद्धम्
प्रश्न 3.
एक बड़े पार्क में, लोग तीन बिन्दुओं (स्थानों) पर केन्द्रित हैं (देखिए आकृति) :
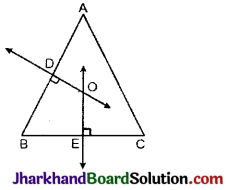
A: जहाँ बच्चों के लिए फिसलपट्टी और झूले हैं।
B: जिसके पास मानव-निर्मित एक झील है।
C: जो एक बड़े पार्किंग स्थल और बाहर निकलने के रास्ते के निकट है।
एक आइसक्रीम का स्टॉल कहाँ लगाना चाहिए ताकि वहाँ लोगों की अधिकतम संख्या पहुँच सके ?
हल:
आइसक्रीम का स्टॉल बिन्दुओं A, B तथा C से समान दूरी पर होना चाहिए तभी समान दूरी के कारण अधिकतम लोग वहाँ पहुँच सकेंगे। इसके लिए भुजा AB तथा BC के लम्ब समद्विभाजक खींचे जाने चाहिए जो एक दूसरे को बिन्दु O पर काटते हैं।
अतः आइसक्रीम का स्टॉल लम्ब समद्विभाजकों के प्रतिच्छेदन बिन्दु पर स्थापित करना चाहिए।
![]()
प्रश्न 4.
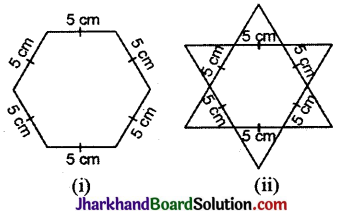
षड्भुजीय और तारे के आकार की रंगोलियों [देखिए आकृति (i) और (ii)] को 1 सेमी भुजा वाले समबाहु त्रिभुजों से भर कर पूरा कीजिए। प्रत्येक स्थिति में, त्रिभुजों की संख्या गिनिए किसमें अधिक त्रिभुज हैं?
हल:
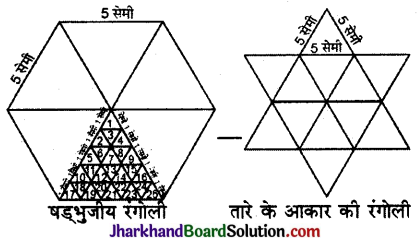
तारे के आकार की रंगोली चित्रों से स्पष्ट है कि षडभुजीय आकृति के सम्मुख शीषों को मिलाने पर प्राप्त विकणों द्वारा उसे 5 सेमी भुजा वाले 6 समबाहु त्रिभुजों में विभक्त किया जा सकता है। तथा तारे की आकृति में निहित पभुजीय आकृति के सम्मुख शीषों को मिलाकर 5 सेमी भुजा वाले 6 अन्य समबाहु त्रिभुजों में विभक्त करने पर उसमें समबाहु त्रिभुजों की संख्या 12 होगी।
पुनः षड्भुजीय आकृति के एक समबाहु त्रिभुज जिसकी भुजा 5 सेमी है, को 1 सेमी भुजा वाले समबाहु त्रिभुजों में विभाजित कर स्पष्ट किया गया है कि 5 सेमी भुजा वाले एक समबाहु त्रिभुज को 1 सेमी भुजा वाले 25 त्रिभुजों में विभाजित किया जा सकता है, तब
स्थिति 1 : षड्भुजीय रंगोली :
इसको 1 सेमी भुजा वाले 6 × 25 = 150 समबाहु त्रिभुजों में बाँटा जा सकता है।
स्थिति 2 : तारे के आकार की रंगोली
5 सेमी भुजा वाले समबाहु त्रिभुजों की संख्या = 12
∴ आकृति में 1 सेमी भुजा वाले समबाहु त्रिभुजों की
संख्या 12 × 25 = 300
स्पष्ट है कि तारे के आकार वाली आकृति में त्रिभुजों की संख्या अधिक है।