Jharkhand Board JAC Class 9 Maths Solutions Chapter 8 चतुर्भुज Ex 8.1 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 8 त्रिभुज Exercise 8.1
प्रश्न 1.
एक चतुर्भुज के कोण 3:59 13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
हल:
माना कोण = (3x)°, (5x)°, (9x)° और (13x)°
अतः 3x + 5x + 9x + 13x = 360°
(चतुर्भुज के अन्तः कोणों का योग)
⇒ 30x = 360°
⇒ x = \(\frac{360^{\circ}}{30}\) = 12°
∴ पहला कोण = 3 × 12° = 36°
दूसरा कोण = 5 × 12° = 60°
तीसरा कोण = 9 × 12° = 108°
चौथा कोण = 13 × 12° = 156°
अंतः चतुर्भुज के कोण क्रमश: 36°, 60°, 108° और 156° हैं।
प्रश्न 2.
यदि एक समान्तर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइये कि वह एक आयत है।
हल:
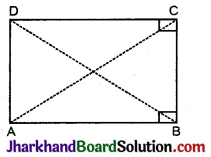
दिया है : समान्तर चतुर्भुज ABCD में,
AC = BD.
सिद्ध करना है: ABCD एक आयत है।
उपपत्ति: ΔABC और ΔDCB में ज्ञात है
AB = DC
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
BC = BC [उभयनिष्ठ]
व AC = DB [दिया है]
ΔABC ≅ ΔDCB (SSS नियम )
⇒ ∠ABC = ∠DCB …..(i)
[सर्वागसम त्रिभुजों के संगत भाग बराबर होते हैं]
लेकिन AB || DC और BC उनको काटती है।
∴ ∠ABC + ∠DCB = 180° …(ii)
[क्रमागत आन्तरिक कोण युग्म]
⇒ 2∠ABC = 180°
⇒ ∠ABC = 90°
इसी प्रकार, ∠ABC = ∠DCB = 90°
⇒ ABCD एक समान्तर चतुर्भुज है, जिसका प्रत्येक कोण 90° है।
∴ ABCD एक आयत है।
इति सिद्धम्।
![]()
प्रश्न 3.
दर्शाइए कि यदि किसी चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें तो वह एक समचतुर्भुज होता है।
हल:
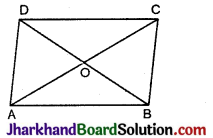
प्रथम विधि : दिया है:
चतुर्भुज ABCD में विकर्ण, AC और BD बिन्दु O पर समद्विभाजित करते हैं तब AO = OC, BO = OD और AC ⊥ BD
सिद्ध करना है : ABCD एक समचतुर्भुज है।
उपपत्ति: चतुर्भुज ABCD के विकर्ण AC और BD एक-दूसरे को समकोण पर समद्विभाजित करते हैं।
∴ AC, रेखाखण्ड BD का लम्ब समद्विभाजक है।
⇒ A और C दोनों B और D से समदूरस्थ हैं।
∴ AB = AD और CB = CD …..(i)
इसी प्रकार BD रेखाखण्ड AC का लम्ब समद्विभाजक है।
⇒ B और D दोनों A और C से समदूरस्य हैं।
⇒ AB = BC और AD = DC …..(ii)
समीकरण (i) एवं (ii) से,
AB = BC = CD = AD …..(iii)
अत: ABCD एक समचतुर्भुज है। इति सिद्धम्।
द्वितीय विधि : पहले हम सिद्ध करेंगे ABCD एक समान्तर चतुर्भुज है।
ΔAOD और ΔCOB में,
AO = OC [दिया है]
OD = OB [दिया है]
तथा ∠AOD = ∠COB [शीर्षाभिमुख कोण]
ΔAOD ≅ ΔCOB (SAS नियम)
या ∠OAD = ∠OCB …..(i)
[सर्वांगसम त्रिभुजों के संगत भाग समान होते हैं]
अब रेखा AC, AD और BC को बिन्दु 4 तथा C पर क्रमश: इस प्रकार काटती है कि
∠OAD = ∠OCB [समीकरण (i) से]
एकान्तर कोण
∴ AD || BC
इसी प्रकार से, AB || CD
अत: ABCD एक समान्तर चतुर्भुज है।
अब हमें यह सिद्ध करना है कि समान्तर चतुर्भुज ABCD एक समचतुर्भुज है।
ΔAOD और ΔCOD में,
OA = OC [दिया है]
∠AOD = ∠COD [समकोण]
तथा OD = CD [उभवनिष्ठ]
ΔAOD ≅ ΔCOD (SAS नियम)
∴ AD = CD …..(1)
[सर्वांगसम त्रिभुज के भाग बराबर होते हैं]
अब ABCD एक समचतुर्भुज है। [ऊपर सिद्ध है]
ABCD और AD = BC
अत: चतुर्भुज ABCD एक समचतुर्भुज है।
इति सिद्धम्।
प्रश्न 4.
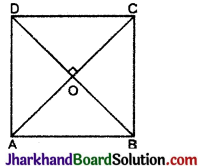
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
हल:
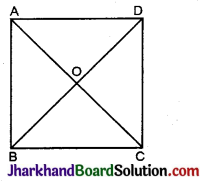
दिया है : वर्ग ABCD में विकर्ण AC और BD परस्पर बिन्दु O पर काटते हैं।
सिद्ध करना है : AC = BD और ∠AOB = 90°.
उपपत्ति: ABCD एक वर्ग है।
∴ AB = BC = CD = DA
और ∠A = ∠B = ∠C = ∠D = 90°.
तब ΔABC और ΔBCD समकोण त्रिभुज हैं।
अब ΔABC और ΔBCD में,
AB = CD (वर्ग की भुजाएँ)
∠B = ∠C (वर्ग के कोण)
BC = BC (उभयनिष्ठ)
∵ΔABC ≅ ΔBCD (SAS नियम)
∴ AC = BD
∵ ABCD एक वर्ग है।
∴ AB = BC = CD = DA
∴ AB = CD और BC = DA
∴ ABCD एक समान्तर चतुर्भुज भी है।
∴ इसके विकर्ण AC तथा BD परस्पर (बिन्दु O पर) समद्विभाजित करेंगे।
∴ AO = BO = CO = DO
अब ΔAOB और ΔBOC में,
AO = CO (सिद्ध किया)
AB = BC (वर्ग की भुजाएँ)
BO = BO (उभयनिष्ठ)
∴ ΔAOB ≅ ΔBOC
⇒ ∠AOB = ∠BOC ….(1)
परन्तु AOC तिर्यक रेखा है।
∴ ∠AOB + ∠BOC = 180° ….(2)
समीकरण (1) व (2) से, ∠AOB = 90°
अतः वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
इति सिद्धम्।
![]()
प्रश्न 5.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर समकोण पर समद्विभाजित करें, तो वह एक वर्ग होता है।
हल:
दिया है:
ABCD एक चतुर्भुज है जिसमें AC = BD, AO = CO, BO = DO तथा ∠COD = 90° है।
सिद्ध करना है: ABCD एक वर्ग है।
यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।
अतः, AB = BC = CD = DA
ΔBAD और ΔABC में
AD = BC [∵ ऊपर सिद्ध किया गया है।]
BD = AC [∵ दिया है]
AB = AB [∵ उभयनिष्ठ ]
अत:, ΔBAD ≅ ΔABC
[∵ SSS सर्वागसमता नियम]
∠BAD = ∠ABC
[∵ सर्वांगसम त्रिभुज के संगत भाग बराबर होते हैं]
परन्तु ∠BAD + ∠ABC = 180°
[∴ अंतः कोण संपूरक होते हैं]
⇒ 2∠ABC = 180° [∵∠BAD = ∠ABC]
∠ABC = \(\frac{180^{\circ}}{2}\) = 90°
एक समचतुर्भुज जिसका एक कोण 90° को हो, एक वर्ग होता है। अत: ABCD एक वर्ग है।
प्रश्न 6.
समान्तर चतुर्भुज ABCD का विकर्ण ∠C कोण A को समद्विभाजित करता है (देखिए आकृति) दर्शाइये कि
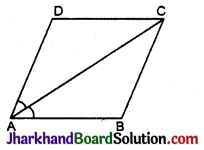
(i) यह ZC को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।
हल:
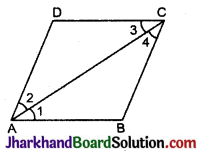
(i) दिया है :
चतुर्भुज ABCD जिसमें विकर्ण AC, ∠A को समद्विभाजित करता है।
सिद्ध करना है विकर्ण AC, ∠C को समद्विभाजित करता है।
उपपत्ति: ∵ ABCD एक समान्तर चतुर्भुज है, अतः AB || DC है।
अब AB || DC और AC उन्हें काटता है।
∴ ∠1 = ∠3 [एकान्तर कोण] …..(i)
पुन: AD || BC और AC उन्हें काटता है।
∴ ∠2 = ∠4 [एकान्तर कोण] …..(ii)
किन्तु AC, ∠A का समद्विभाजक है।
∴ ∠1 = ∠2 ….(iii)
समीकरण (i), (ii) और (iii) से,
∠3 = ∠4
अत: विकर्ण AC, ∠C को समद्विभाजित करता है।
(ii) सिद्ध करना है : ABCD एक समचतुर्भुज है।
समीकरण (i), (ii) और (iii) से,
∠1 = ∠2 = ∠3 = ∠4
अब ΔABC में,
∠1 = ∠4
⇒ AB = BC ….(iv)
[त्रिभुज में समान कोणों के सामने की भुजाएँ]
इसी प्रकार ΔADC मैं,
AD = DC ….(v)
और ABCD एक समान्तर चतुर्भुज है,
∴ AB = CD और AD = BC ….. (vi)
समी. (iv), (v) व (vi) से,
AB = BC = CD = DA.
अत: ABCD एक समचतुर्भुज है। इति सिद्धम्।
![]()
प्रश्न 7.
ABCD एक समचतुर्भुज है। दर्शाइए कि विकर्ण AC सम्मुख कोणों A और C को समद्विभाजित करता है तथा विकर्ण BD सम्मुख कोणों B और D को समद्विभाजित करता है।
हल:
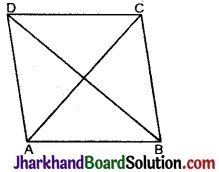
दिया है : समान्तर चतुर्भुज ABCD, विकर्ण AC तथा BD है।
सिद्ध करना है:
(i) विकर्ण AC, ∠A और कोण ∠C को समद्विभाजित करता है।
(ii) विकर्ण BD, ∠B और ∠D को समद्विभाजित करता है।
उपपत्ति: ΔADC में,
AD = DC
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
∠DAC = ∠DCA ….(i)
[त्रिभुज में बराबर भुजाओं के सम्मुख कोण]
अब AB || DC और AC उन्हें समद्विभाजित करती है।
∠BCA = ∠DAC …..(ii)
[एकान्तर कोण]
समीकरण (i) एवं (ii) से,
∠DCA = ∠BCA
⇒ AC, कोण C को समद्विभाजित करती है।
ΔABC में, AB = BC
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
∠BCA = ∠BAC …..(iii)
[त्रिभुज में समान भुजाओं के सम्मुख कोण]
समीकरण (ii) और (iii) से,
∠BAC = ∠DAC
या AC, ∠A को समद्विभाजित करता है।
इसी प्रकार, विकणं BD, ∠B तथा ∠D को समद्विभाजित करता है।
इति सिद्धम्।
प्रश्न 8.
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि
(i) ABCD एक वर्ग है।
(ii) विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
हल:
दिया है: ABCD एक आयत है जिसमें
∠1 = ∠2 तथा ∠3 = ∠4 है।
सिद्ध करना है: ABCD एक वर्ग है।
∠1 = ∠4 ….(1) [∵ एकांतर कोण]
∠3 = ∠4 …..(2) [∵ दिया है]
∠1 = ∠3 …(3)
[∵ समीकरण (1) और (2) से]
ΔADC में,
∠1 = ∠3 [∵ समीकरण (3) से]
DC = AD
[∵ त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।]
एक आयत जिसकी आसन्न भुजाएँ समान हों, वर्ग होता है अत:, ABCD एक वर्ग है।
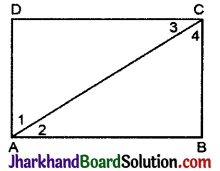
(ii) सिद्ध करना है : विकर्ण BD दोनों कोण B और D को समद्विभाजित करता है।
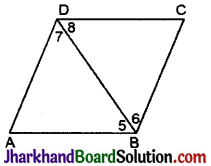
∠5 = ∠8 …. (4) [∵ एकांतर कोण]
ΔADB में,
AB = AD [∵ ABCD एक वर्ग है]
∠7 = ∠5 …..(5)
[∵ त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
अत:, ∠7 = ∠8 …(6)
[∵ समीकरण (4) और (5) से]
तथा ∠7 = ∠6 ….(7) [∵ एकांतर कोण ]
अत:, ∠5 = ∠6 ….(8)
[∵ समीकरण (5) और (7) से]
अत:, समीकरण (6) और (8) से विकर्ण BD दोनों कोणों B और D को सद्विभाजित करता है।
![]()
प्रश्न 9.
समान्तर चतुर्भुज ABCD के विकर्ण BD पर दो बिन्दु P और Q इस प्रकार स्थित हैं कि DP (देखिए आकृति)। दर्शाइए कि :
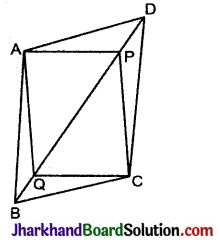
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ एक समान्तर चतुर्भुज है।
हल:
दिया है : ABCD एक समान्तर चतुर्भुज है। विकर्ण BD पर बिन्दु P और Q इस प्रकार स्थित हैं कि DP = BQ.
सिद्ध करना है:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ एक समान्तर चतुर्भुज है।
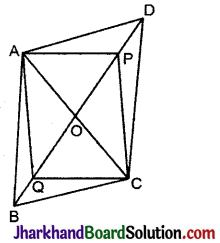
रचना : A और C को मिलाया जो BD से O बिन्दु पर मिलती है।
उपपत्ति: (i) ΔAPD और ΔCQB में,
AD = CB
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
∠QBC = ∠ADP (एकान्तर कोण)
DP = BQ [दिया है]
ΔAPD ≅ ΔCQB. (SAS नियम)
इति सिद्धम्।
AP = CQ [सर्वागसम Δ के संगत भाग]
(ii) AP = CQ [सिद्ध किया गया है।]
(iii) ΔAQB और ΔCPD में,
∵ AB = CD
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
∠ABQ = ∠CDP [AB || CD]
[एकान्तर कोण हैं]
और BQ = DP [दिया है]
ΔAQB ≅ ΔCPD. (SAS नियम)
इति सिद्धम्।
(iv) ∵ ΔAQB ≅ ΔCPD,
∴ AQ = CP [सर्वांगसम त्रिभुज के संगत भाग]
इति सिद्धम्।
(v) चूँकि समान्तर चतुर्भुज के विकर्ण AC तथा BD एक दूसरे को बिन्दु O पर समद्विभाजित करते हैं।
∴ OB = OD
किन्तु BQ = DP [दिया है]
⇒ OB – BQ = OD – DP या OQ = OP
इति सिद्धम्।
प्रश्न 10.
ABCD एक समान्तर चतुर्भुज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमश: लम्ब हैं (देखिए आकृति)। A दर्शाइए कि :
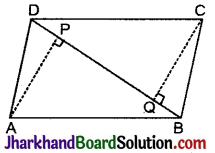
(i) ΔAPB ≅ ΔCQD तथा
(ii) AP = CQ.
हल:
(i) ∵ ABCD समान्तर चतुर्भुज है।
∴ DC || AB
∵ DC || AB और तिर्यक रेखा BD उन्हें B और D पर प्रतिच्छेदित करती है।
∴ ∠ABD = ∠BDC [एकान्तर कोण]
अब, ΔAPB और ΔCQD में,
∠ABP = ∠QDC [∵ ∠ABD = ∠BDC]
∠APB = ∠CQD [प्रत्येक 90°]
और AB = CD
[समान्तर चतुर्भुज की सम्मुख भुजाएँ ।
ΔAPB ≅ ΔCQD. (AAS नियम)
इति सिद्धम्।
(ii) ∵ ΔAPB ≅ ΔCQD
∴ AP = CQ इति सिद्धम्।
![]()
प्रश्न 11.
ΔABC और ΔDEF में, AB = DE, AB || DE, BC = EF और BC || EF हैं। शीषों A, B और C को क्रमशः शीर्षो D, E और F से जोड़ा जाता है (देखिए आकृति)। दर्शाइए कि :
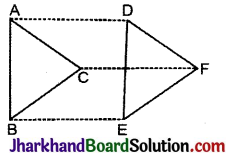
(i) ABED एक समान्तर चतुर्भुज है।
(ii) BEFC एक समान्तर चतुर्भुज है।
(iii) AD || CF और AD = CF है।
(iv) ACFD एक समान्तर चतुर्भुज है।
(v) AC = DF है।
(vi) ΔABC ≅ ΔDEF है।
हल:
दिया है : दो ΔABC और ΔDEF इस प्रकार हैं कि AB = DE और AB || DE साथ ही BC = EF और BC || EF.
सिद्ध करना है : (i) ABED समान्तर चतुर्भुज है।
(ii) BEFC समान्तर चतुर्भुज है।
(iii) AD || CF और AD = CF है।
(iv) ACFD समान्तर चतुर्भुज है।
(v) AC = DF है।
(vi) ΔABC ≅ ΔDEF है।
उपपत्ति: (i) चतुर्भुज ABED में,
AB = DE और AB || DE (सम्मुख भुजा युग्म)
अत: ABED समान्तर चतुर्भुज है। इति सिद्धम्।
(ii) अब चतुर्भुज BEFC में,
BC = EF और BC || EF (सम्मुख भुजा युग्म)
⇒ BEFC समान्तर चतुर्भुज है। इति सिद्धम्।
(iii) अब, AD = BE और AD || BE …..(i)
[∵ ABED समान्तर चतुर्भुज है।]
और CF = BE और CF || BE …(ii)
[∵ BEFC एक समान्तर चतुर्भुज है।]
समीकरण (i) और (ii) से,
AD = CF और AD || CF. इति सिद्धम्।
(iv) ∵ AD = CF और AD || CF (सम्मुख भुजा युग्म)
∴ ACFD एक समान्तर चतुर्भुज है। इति सिद्धम्।
(v) ∵ ACFD एक समान्तर चतुर्भुज है।
∴ AC = DF और AC || DF. इति सिद्धम्।
(vi) ΔABC और ΔDEF मैं,

और CA = FD
ΔABC ≅ ΔDEF (sss नियम)
इति सिद्धम्।
![]()
प्रश्न 12.
ABCD एक समलम्ब चतुर्भुज है, जिसमें AB || DC और AD = BC है (देखिए आकृति)। दर्शाइए कि
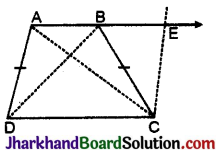
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) विकर्ण AC = विकर्ण BD है।
[संकेत : AB को बढ़ाइए और C से होकर DA के समान्तर एक रेखा खींचिए, जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करे।]
हल:
दिया है: ABCD एक समलम्ब चतुर्भुज है, जिसमें AB || DC और AD = BC है।
सिद्ध करना है:
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) विकर्ण AC = विकर्ण BD है।
रचना: AB को E तक इस प्रकार आगे बढ़ाया कि AE = DC और CE || AD खींची।
उपपत्ति: (i) ∵ AD || CE और तिर्यक रेखा AE उन्हें क्रमश: A और E पर प्रतिच्छेदित करती है।
∴ ∠A + ∠E = 180° …..(i)
(अन्तः संगत कोण)
चूँकि AB || CD और AD || CE, अतः AECD समान्तर चतुर्भुज है।
⇒ AD = CE
⇒ BC = CE
तथा AD = BC (दिया है)
इस प्रकार, ΔBCE में,
BC = CE
⇒ ∠CBE = ∠CEB
(समान भुजाओं के सम्मुख कोण)
⇒ 180°- ∠B = ∠E
⇒ ∠B + ∠E = 180° ……(ii)
समीकरण (i) एवं (ii) से,
∠A = ∠B. इति सिद्धम् ।
∠A + ∠E = ∠B + ∠E
(ii) ∵ ∠A = ∠B
⇒ ∠BAD = ∠ABC
⇒ 180° – ∠BAD = 180° – ∠ABC
⇒ ∠ADC = ∠BCD
⇒ ∠D = ∠C इति सिद्धम्।
(iii) ΔABC और ΔBAD मैं,
∵ BC = AD [दिया है]
AB = BA [उभयनिष्ठ]
तथा ∠A = ∠B [सिद्ध किया है]
ΔABC ≅ ΔBAD (SAS नियम)
इति सिद्धम्।
(iv) ∵ ΔABC ≅ ΔBAD
∴ AC = BD इति सिद्धम्।
अन्त: खण्ड : चित्र में यदि समतल में दो रेखाएँ AB और CD (समान्तर या प्रतिच्छेदी) दी हुई हों और रेखा LM उन्हें अलग-अलग बिन्दुओं P और Q पर प्रतिच्छेद करती है, तो रेखाखण्ड PQ दी हुई रेखाओं पर तीसरी रेखा द्वारा बनाया गया अन्त: खण्ड कहलाता है।