Jharkhand Board JAC Class 9 Maths Solutions Chapter 10 वृत्त Ex 10.4 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 10 वृत्त Exercise 10.4
प्रश्न 1.
5 सेमी और 3 सेमी त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेदित करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 सेमी है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।
हल:
O तथा O’ केन्द्रों वाले वृत्तों की त्रिज्याएँ OA तथा O’A क्रमश: 5 सेमी व 3 सेमी हैं। OO’ = 4 सेमी है।
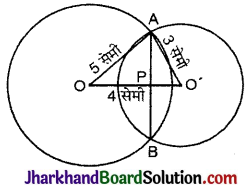
ΔOAO’ में पाइथागोरस प्रमेय से,
(OA)2 = (O’A)2 + (OO’)2
52 = 32 + 42
25 = 9 + 16 = 25
अत: ΔOAQ’ समकोण त्रिभुज है, जिसमें सबसे बड़ी भुजा OA कर्ण है, तब ∠AO’O समकोण है।
∴ बिन्दु P और केन्द्र O’ सम्पाती होंगे
अतः AP = AO’ = 3 सेमी
∴ जीवा की लम्बाई = 2 × AP
= 2 × 3 = 6 सेमी
![]()
प्रश्न 2.
यदि एक वृत्त की दो समान जीवाऐं वृत्त के अन्दर प्रतिच्छेदित करें, तो सिद्ध कीजिए कि एक जीवा के दोनों खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं।
हल:
दिया है वृत्त C (O, r) में जीवा AB = जीवा CD जो एक-दूसरे को बिन्दु पर प्रतिच्छेदित करती हैं।
सिद्ध करना है:
(i) CP = AP
(ii) PB = PD.
रचना: OM ⊥ AB
ON ⊥ CD खींचे। OP को मिलाया।
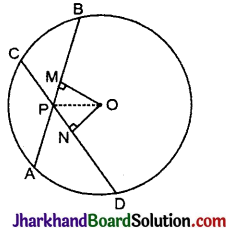
उपपत्ति: AM = MB = \(\frac{1}{2}\)AB
तथा CN = ND = \(\frac{1}{2}\)CD
[केन्द्र से खींचा गया लम्ब जीवा को समद्विभाजित करता है]

[∵ AB = CD (दिया है)]
ΔOMP तथा ΔONP में, OM = ON
[एक वृत्त की समान जीवाएँ केन्द्र से समान दूरी पर स्थित होती हैं।]
∠OMP = ∠ONP [प्रत्येक 90°]
OP = OP [उभयनिष्ठ]
ΔOMP ≅ ΔONP (RHS नियम से)
अतः MP = PN ……(2)
समीकरण (1) मैं (2) जोड़ने पर,
MB + MP = ND + PN
या BP = PD ……(2)
समीकरण (1) में से (2) को घटाने पर,
AM – MP= CN – PN
AP = CP ……(1)
अत: (i) AP = CP और (ii) PB = PD. इति सिद्धम्।
प्रश्न 3.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेदित करें, तो सिद्ध कीजिए कि प्रतिच्छेदित बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती हैं।
हल:
दिया है: वृत्त C (O, r) में जीवा AB = जीवा CD जो परस्पर P बिन्दु पर प्रतिच्छेदित करती हैं।
सिद्ध करना है: ∠OPE = ∠OPF.
रचना : OE ⊥ AB तथा OF ⊥ CD खींचे और OP को मिलाया।
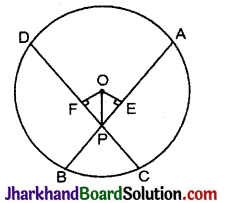
उपपत्ति: ΔOEP तथा ΔOFP में,
∠OEP = ∠OFP [प्रत्येक 90°]
OP = OP [उभयनिष्ठ]
OE = OF
[एक वृत्त की समान जीवाएँ केन्द्र से समान दूरी पर स्थित होती हैं]
∴ ΔOEP ≅ ΔOFP (RHS नियम से)
अतः ∠OPE = ∠OPF इति सिद्धम्।
![]()
प्रश्न 4.
यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्तों) को, जिनका केन्द्र O है, A, B, C और D पर प्रतिच्छेदित करे, तो सिद्ध कीजिए AB = CD (देखिए आकृति)।
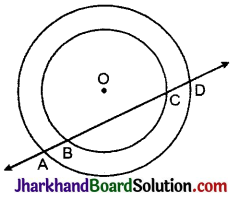
हल:
OM ⊥ AD खींचा।
BC छोटे वृत्त की जीवा है तथा OM ⊥ BC
BM = CM ……(1)
AD बड़े वृत्त की जीवा है तथा OM ⊥ AD
AM = DM ……(2)
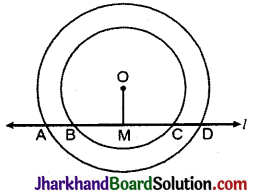
(∵ वृत्त के केन्द्र से जीवा पर डाला गया लम्ब जीवा को समाद्विभाजित करता है)
समीकरण (2) में से (1) को घटाने पर,
AM – BM = DM – CM
∴ AB = CD. इति सिद्धम्।
प्रश्न 5.
एक पार्क में बने 5 मीटर त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच प्रत्येक की दूरी 6 मीटर हो, तो रेशमा और मनदीप के बीच की दूरी क्या है ?
हल:
दिया है: पार्क में 5 मीटर त्रिज्या का एक वृत्त है जिसका केन्द्र O है। तीन लड़कियाँ रेशमा, सलमा और मनदीप वृत्त पर क्रमश: A, B व C स्थानों पर खड़ी हैं। रेशमा और सलमा के बीच की दूरी AB = 6 मीटर तथा सलमा और मनदीप के बीच दूरी BC = 6 मीटर है।
ज्ञात करना है: रेशमा और मनदीप के बीच की दूरी = AC
गणना : त्रिज्याएँ OA और OB खींचीं और माना त्रिज्या OB, AC को बिन्दु P पर काटती है।
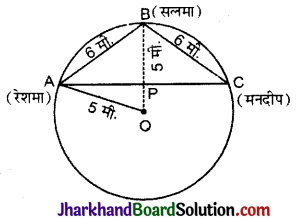
ΔOAB में, OA = 5 मीटर (त्रिज्या), OB = 5 मीटर (त्रिज्या) तथा AB = 6 मीटर।
माना OP = x, तब BP = (5 – x)
ΔABP मै,
∠P = 90°
∴ AP2 = AB2 – BP2 = (6)2 – (5 – x)2
= 36 – (25 – 10x + x2)
AP2 = 11 + 10x – x2 ……(1)
पुन: ΔAPO में,
AP2 = AO2 – OP2
AP2 = 52 – x2 = 25 – x2 ……(2)
समी. (1) तथा (2) से,
11 + 10x – x2 = 25 – x2
या 10x = 14
x = \(\frac{14}{10}\) = \(\frac{7}{5}\)
x का मान समीकरण (2) में रखने पर,

अतः रेशमा और मनदीप के बीच की दूरी 9.6 मीटर है।
![]()
प्रश्न 6.
20 मीटर त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कॉलोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
हल:
दिया है: O केन्द्र वाला एक वृत्ताकार पार्क जिसकी त्रिज्या OA = OB = 20 मीटर है। वृत्त की परिधि पर तीन लड़के एक-दूसरे से
बराबर दूरी पर A, B व C स्थानों पर बैठे हैं।
अत: AB = BC = CA.
ज्ञात करना है: डोरी की लम्बाई AB.
रचना: AM ⊥ BC खींचा तथा BO को मिलाया।
गणना: चूँकि ΔABC एक समबाहु त्रिभुज है।
माना इसकी प्रत्येक भुजा = x
ऊँचाई AM = \(\sqrt{3}\)x
अब OM = AM – OA
= (\(\sqrt{3}\)x – 20) मीटर
समकोण ΔOBM में,
OB2 = BM2+ OM2
⇒ 202 = x2 + (\(\sqrt{3}\)x – 20)2
⇒ 400 = x2 + 3x2 – 40\(\sqrt{3}\)x + 400
⇒ 4x2 – 40\(\sqrt{3}\)x = 0
⇒ 4x (x – 10\(\sqrt{3}\)) = 0
या तो x = 0, (असंभव)
या x – 10\(\sqrt{3}\) = 0
⇒ x = 10\(\sqrt{3}\)
अब BC = 2BM = 2x = 20\(\sqrt{3}\) मीटर
अतः प्रत्येक फोन की डोरी की लम्बाई = 20\(\sqrt{3}\) मीटर।