JAC Class 10 Maths Important Questions Chapter 1 वास्तविक संख्याएँ

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 1 वास्तविक संख्याएँ Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 1 वास्तविक संख्याएँ

लघुत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
सिद्ध कीजिए कि प्रत्येक तीन क्रमागत धनात्मक पूर्णांकों में से एक 3 से विभाज्य है।
हल :
माना कि n, n + 1, n + 2 तीन क्रमागत धनात्मक पूर्णांक हैं।
∵ हम जानते हैं कि n, 3q या 3q + 1 या 3q + 2 के रूप का होता है।
∴ निम्नलिखित तीन स्थितियाँ सम्भव हैं।
स्थिति 1. जब n = 3q, जो कि 3 से विभाज्य है।
n + 1 = 3q + 1, 3 से विभाज्य नहीं है।
n + 2 = 3q + 2, 3 से विभाज्य नहीं है।
इस स्थिति में n, 3 से विभाज्य है परन्तु n + 1 और n + 2, 3 से विभाज्य नहीं हैं।
स्थिति 2. जब n = 3q + 1
इस स्थिति में n + 2 = 3q + 1 + 2 = 3(q + 1) जो कि 3 से विभाज्य है परन्तु तथा n + 1, 3 से विभाज्य नहीं है।
स्थिति 3. जब n = 3q + 2
इस स्थिति में n + 1 = 3q + 1 + 2 = 3(q + 1), 3 से
विभाज्य है परन्तु n या n + 2, 3 से विभाज्य नहीं है।
अत: n, n + 1 तथा n + 2 में से एक 3 से विभाज्य है।

प्रश्न 2.
सिद्ध कीजिए कि \(\sqrt{3}\) एक अपरिमेय संख्या
हल :
माना कि \(\sqrt{3}\) एक परिमेय संख्या है।
हम ऐसी सह अभाज्य (Co-prime) संख्याएँ a और b ज्ञात करते हैं कि
\(\sqrt{3}\) = \(\frac{a}{b}\) [जहाँ b ≠ 0]
दोनों पक्षों का वर्ग करने पर
3 = \(\frac{a^2}{b^2}\)
⇒ a² = 3b²
अतः 3, a² को विभाजित करता हैं
⇒ 3, a को विभाजित करेगा।
माना कि a = 3c (जहाँ c कोई पूर्णांक है)
⇒ a² = 9c²
⇒ 3b² = 9c² [∵ a² = 3b²]
⇒ b² = 3c²
अत: 3, b² को विभाजित करता है।
⇒ 3, b को विभाजित करेगा।
अतः a और b में कम से कम एक उभयनिष्ठ गुणनखण्ड 3 है।
परन्तु यह इस तथ्य का विरोध करता है कि a और b में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखण्ड नहीं है। अतः हमारी परिकल्पना गलत है।
अतः \(\sqrt{3}\) एक अपरिमेय संख्या है। इति सिद्धम् ।

प्रश्न 3.
संख्याओं 180, 72 व 252 का HCF और LCM ज्ञात कीजिए।
हल :
संख्याओं के गुणनखण्ड करने पर

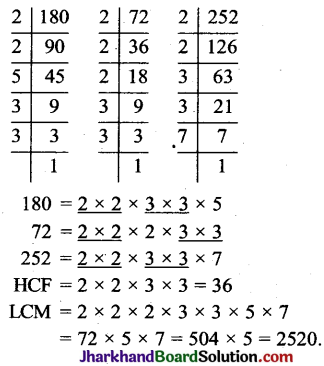
प्रश्न 4.
अभाज्य गुणनखण्ड विधि द्वारा पूर्णांक 375 और 675 का HCF ज्ञात कीजिए।
हल :
अभाज्य गुणनखण्ड विधि द्वारा

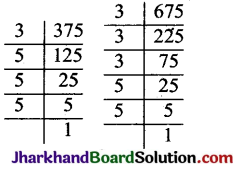
375 = 3 × 5 × 5 × 5 = 3 × 5³
675 = 3 × 3 × 3 × 5 × 5 = 3³ × 5²
अंतः म. स. 3 × 5² = 3 × 25 = 75

प्रश्न 5.
सिद्ध कीजिए \(\sqrt{6}\) एक अपरिमेय संख्या है।
हल :
माना \(\sqrt{6}\) एक परिमेय संख्या है।
∴ हम दो पूर्णांक r और s ऐसे ज्ञात कर सकते हैं कि हो तथा s ≠ 0 हो। यहाँ और सह अभाज्य हैं, अर्थात् इनमें 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखण्ड नहीं है।
अब \(\sqrt{6}\) = \(\frac{r}{s}\)
दोनों पक्षों का वर्ग करने पर
6 = \(\frac{r^2}{s^2}\)
⇒ 6s² = r²
⇒ s² = \(\frac{r^2}{6}\)
⇒ 6, r² को विभाजित करता है।
⇒ इसलिए 6, r को भी विभाजित करता है।
⇒ 6, r का एक गुणनखण्ड है। ………..(A)
माना r = 6m
⇒ 6s² = (6m)²
⇒ 6s² = 36m²
⇒ s² = 6m²
⇒ m² = \(\frac{s^2}{6}\)
⇒ 6, s² को विभाजित करता है।
⇒ इसलिए 6, s को भी विभाजित करता है।
⇒ 6, s का एक गुणनखण्ड है। …(B)
समीकरण (A) और (B) अवलोकन करने पर हम पाते हैं कि r और s में 1 के अतिरिक्त एक अन्य उभयनिष्ठ गुणनखण्ड 6 है। परन्तु इससे इस तथ्य का विरोधाभास प्राप्त होता है कि r और s में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखण्ड नहीं है। इसका तात्पर्य है कि हमने एक त्रुटिपूर्ण कल्पना की थी।
अत: \(\sqrt{6}\) एक अपरिमेय संख्या है।

प्रश्न 6.
दो पूर्णांक संख्याओं का HCF व LCM क्रमशः 12 और 36 हैं, यदि एक पूर्णांक 48 है, तो दूसरा पूर्णांक ज्ञात कीजिए। (मा. शि. बो. राज. 2017 )
हल :
दिया है, HCF = 12, LCM = 336, एक पूर्णांक संख्या = 48
∴ HCF × LCM = पहली संख्या × दूसरी संख्या
⇒ 12 × 36 = 48 × दूसरी संख्या
अतः दूसरी संख्या = \(\frac{12 \times 36}{48}\) = 9

प्रश्न 7.
किसी परेड़ में 612 सदस्यों वाली एक सेना की टुकड़ी को 48 सदस्यों वाले एक बैंड के पीछे मार्च करना है। दोनों समूहों को समान संख्या वाले स्तम्भों में मार्च करना है। उन स्तम्भों की अधिकतम संख्या, जिसमें वे मार्च कर सकते हैं, क्या है?
हल :
स्तम्भों में अधिकतम संख्या ज्ञात करने के लिए में 612 और 48 का म.स. ज्ञात करना है।

∴ म. स. (612, 48) = 12
अतः अधिकतम स्तम्भों की संख्या 12 है।

प्रश्न 8.
वह सबसे छोटी संख्या लिखिए जो 306 तथा 657 से पूर्णतया विभाजित हो ।
हल :
सबसे छोटी संख्या जो 306 और 657 दोनों से पूर्णतया विभाजित होगी वह है :
ल. स. (657, 306)
657 = 3 × 3 × 73
306 = 3 × 3 × 2 × 17
अत: ल. स. (657, 306) = 3 × 3 × 73 × 2 × 17
= 22338

प्रश्न 9.
\(\sqrt{2}\) तथा \(\sqrt{3}\) के बीच में स्थित एक परिमेय संख्या ज्ञात कीजिए।
हल:
\(\sqrt{2}\) = 1.414
\(\sqrt{3}\) = 1.732
\(\sqrt{2}\) तथा \(\sqrt{3}\) के बीच परिमेय संख्या है,
= 1.5 (∵ 1.414 < 1.5 < 1.732)

प्रश्न 10.
दर्शाइए कि प्रत्येक विषम धनपूर्णांक (4q + 1) अथवा (4q + 3) के रूप का होता है, वहाँ q कोई पूर्णांक है।
हल :
मान लीजिए कि ‘a’ एक विषम धन पूर्णांक है तथा b = 4 है।
a तथा b में विभाजन एल्गोरिथ्म का प्रयोग करने पर,
a = bq + r, r < b
∴ a = 4q + r
∵ 0 ≤ r ≤ 4 इसलिए संभावित शेषफल 0, 1, 2, 3 हैं।
∵ a = 4q, 4q + 1, 4q + 2, 4q + 3; जहाँ q भागफल है।
∵ a एक विषम धन पूर्णांक 4q + 1, 4q + 3 के प्रकार का होगा।

प्रश्न 11.
दो धनपूर्णांक a तथा b जहाँ a = x³y² तथा b = xy³ के रूप में लिखे जा सकते हैं, जहाँ x, y अभाज्य संख्याएँ हैं, तो ल.स. (LCM) (a, b) का मान ज्ञात कीजिए ।
हल :
दिया है, a = x²y², b = xy³, और
म. स. (HCF) = xy²
∵ म. स. × ल. स. = a × b
xy² × ल. स. = x³y² × xy³

प्रश्न 12.
छोटी से छोटी अभाज्य संख्या तथा छोटी-से-छोटी भाज्य संख्या का म.स. (HCF) क्या है?
हल :
छोटी से छोटी अभाज्य संख्या = 2 तथा छोटी से
भाज्य संख्या = 4

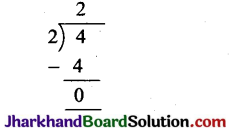
अत: म. स. (HCF) = 2

प्रश्न 13.
404 तथा 96 का म. स. (HCF) तथा ल. स. (LCM) ज्ञात कीजिए तथा निम्न का सत्यापन कीजिए :
HCF × LCM = दोनों दी गई संख्याओं का गुणनफल
इल :
404 व 96 के अभाज्य गुणनखण्ड :

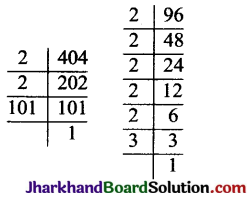
404 = 2 × 2 × 101 × 1
96 = 2 × 2 × 2 × 2 × 3 × 1
म. स. = 2 × 2 × 1 = 4
ल. स. = 2 × 2 × 101 × 2 × 2 × 2 × 3
= 9696
सत्यापन:
∵ HCF × LCM – दोनों दी गई संख्याओं का गुणनफल
⇒ 4 × 9696 = 404 × 96
⇒ 38784 = 38784
अतः दिया कथन सत्यापित हुआ। इति सिद्धम्

रिक्त स्थानों की पूर्ति कीजिए-

प्रश्न (क)

1. यूक्लिड विभाजन प्रमेयिका पूर्णांकों की ……………. के संबंध में है।
2. वह सबसे बड़ा धनात्मक पूर्णांक जो दिए हुए दो धनात्मक पूर्णांकों को पूर्णत: विभाजित कर देता है, संख्याओं का ………………… समापवर्तक कहलाता है।
3. सबसे छोटी भाज्य सम संख्या ………………… तथा सबसे छोटी भाग्य विषम संख्या …………………. है।
4. जिन संख्याओं का दशमलव प्रसार विभाजन प्रक्रिया के परिमित चरणों के बाद समाप्त हो जाता है ……………… दशमलव कहलाती है।
5. ऐसा दशमलव प्रसार जिसका अंत नहीं होता तथा भागफल में अंकों का एक पुनरावृत्ति खंड प्राप्त होता, …………… प्रसार कहलाता है।

हल :

1. विभाज्यता,
2. महत्तम,
3. 4, 9,
4. सांत,
5. असांत आवर्ती

निम्न में सत्य / असत्य कथन बताइए :

प्रश्न (ख)

1. प्रमेयिका एक सत्य कथन है, जिसका प्रयोग अन्य कथनों को सिद्ध करने के लिए किया जाता है।
2. संख्या 2 सबसे छोटी अभाज्य संख्या है।
3. दो या दो से अधिक संख्याओं का ल.स. वह छोटी से ‘छोटी संख्या होती है, जो दी गई संख्याओं से पूर्णतया विभाजित होती है।
4. असांत अनावर्ती दशमलव प्रसार वाली संख्याओं को परिमेय संख्या कहते हैं।
5. यदि किसी परिमेय संख्या को किसी अन्य शून्येत्तर परिमेय संख्या से भाग दिया जाए, तो प्राप्त संख्या हमेशा परिमेय होगी।

हल :

1. सत्य
2. सत्य
3. सत्य
4. असत्य
5. सत्य

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
दिया है, HCF (156, 78) = 78, तो LCM (156, 78) का मान है :
(A) 156
(B) 78
(C) 156 × 78
(D) 156 × 2
हल :
∵ HCF × LCM = संख्याओं का गुणनफल
⇒ 78 × LCM = 156 × 78
⇒ LCM = \(\frac{156 \times 78}{78}\) = 156
अत: सही विकल्प (A) है।

प्रश्न 2.
\(\frac{1095}{1168}\) का सरलतम रूप है :
(A) \(\frac{17}{26}\)
(B) \(\frac{25}{26}\)
(C) \(\frac{13}{26}\)
(D) \(\frac{15}{16}\)
हल :
1095 और 1168 का म. स. = 73

∴ सही विकल्प (D) है।

प्रश्न 3.
निम्न में से कौन-सी परिमेय संख्या को सांत दशमलव के रूप में व्यक्त किया जा सकता है?
(A) \(\frac{124}{165}\)
(B) \(\frac{131}{30}\)
(C) \(\frac{2027}{625}\)
(D) \(\frac{1625}{462}\)
हल :
\(\frac{124}{165}\) = \(\frac{124}{3^1 \times 5^1 \times 11^1}\)
गुणनखंड 2ⁿ × 5ⁿ के रूप में नहीं है।
\(\frac{131}{30}\) = \(\frac{131}{2^1 \times 3^1 \times 5^1}\)
गुणनखंड 2ⁿ × 5ⁿ के रूप में है।
\(\frac{2027}{625}\) = \(\frac{2027}{2^0 \times 5^4}\)
गुणनखंड 2ⁿ × 5ⁿ के रूप में नहीं है।
\(\frac{1625}{462}\) = \(\frac{1625}{2^1 \times 3^1 \times 7^1 \times 11^1}\)
गुणनखंड 2ⁿ × 5ⁿ के रूप में नहीं है।
अत: सही विकल्प (C) है।

प्रश्न 4.
वह बड़ी से बड़ी संख्या, जिससे 245 तथा 1029 को भाग देने पर क्रमशः 5 एवं शेष बचे है:
(A) 15
(B) 60
(C) 9
(D) 5
हल :
∵ प्रत्येक स्थिती में 5 शेष बचता है।
∴ 245 – 5 = 240 तथा 1029 – 9 = 1020
अभीष्ट संख्या 240 और 1020 का म. स. है ।

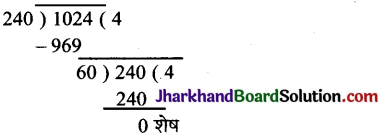
∴ म.स. = 5
अत: सही विकल्प (D) है।

प्रश्न 5.
225 को निम्न रूप में व्यक्त किया जा सकता है:
(A) 5 × 3².
(B) 5² × 3
(C) 5² × 3²
(D) 5 × 3
हल :
अभाज्य गुणनखण्ड विधि से

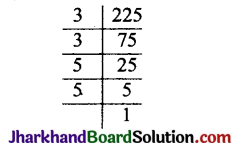
∴ 225 = 3 × 3 × 5 × 5 = 3² × 5²
अत: सही विकल्प (c) है।

प्रश्न 6.
\(2 . \overline{35}\) है एक :
(A) पूर्णांक
(B) परिमेय संख्या
(C) अपरिमेय संख्या
(D) प्राकृत संख्या
हल :
\(2 . \overline{35}\) का प्रसार असांत आवर्ती है।
∴ यह एक परिमेय संख्या है।
अतः विकल्प (B) सही है।

प्रश्न 7.
144 तथा 198 का महत्तम समापवर्तक है:
(A) 9
(B) 18
(C) 6
(D) 12
हल :

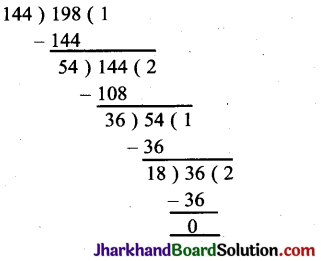
∴ म. स. = 18
अत: विकल्प (B) सही है।

प्रश्न 8.
दो संख्याओं का म. स. 27 है तथा उनका ल.स. 162 है। यदि एक संख्या 54 है, तो दूसरी संख्या है :
(A) 36
(B) 35
(C) 9
(D) 81
हल :
∵ म. स. × ल. स. = पहली संख्या × दूसरी संख्या
⇒ 27 × 162 = 54 × दूसरी संख्या
⇒ दूसरी संख्या = \(\frac{27 \times 162}{54}\) = 81
अत: सही विकल्प (D) है।

प्रश्न 9.
2\(\sqrt{3}\) एक :
(A) पूर्णांक है
(B) परिमेय संख्या है
(C) अपरिमेय संख्या है
(D) एक पूर्ण संख्या है.
हल :
एक परिमेय संख्या (2) और अपरिमेय संख्या (\(\sqrt{3}\)) का गुणनफल एक अपरिमेय संख्या होती है। अत: सही विकल्प (c) है।

प्रश्न 10.
संख्या \(\frac{3}{2^5 \times 5^2}\) का दशमलव प्रसार दशमलव के कितने स्थानों के बाद सांत होगा ?
(A) 2
(B) 4
(C) 5
(D) 1
हल :
यहाँ हर = 2⁵ × 5²
∴ दशमलव प्रसार 5 दशमलव स्थानों के बाद सांत होगा।
अतः सही विकल्प (c) है।

प्रश्न 11.
एक अभाज्य संख्या के कुल गुणनखण्डों की संख्या है :
(A) 1
(B) 0
(C) 2
(D) 3
हल :
दो 1 और स्वयं वही संख्या।
अत: सही विकल्प (c) है।

प्रश्न 12.
12, 21, 15 का म. स. और ल. स. है:
(A) 3, 140
(B) 12,420
(C) 3, 420
(D) 420, 3
हल :
यहाँ,
12 = 2 × 2 × 3
21 = 3 × 7
15 = 3 × 5
∴ म. स. = 3
ल. स. = 22 × 3 × 5 × 7
= 420
अत: सही विकल्प (C) है।

प्रश्न 13.
संख्या 196 के अभाज्य गुणनखण्ड में अभाज्य गुणनखण्डों की घातों का योग है :
(A) 3
(B) 4
(C) 5
(D) 2
हल :

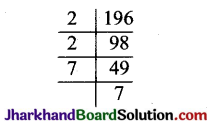
196 = 2 × 2 × 7 × 7= 2² × 7²
घातों का योग = 2 + 2 = 4
अत: सही विकल्प (B) है।

प्रश्न 14.
यूक्लिड विभाजन प्रमेविका के अनुसार दो धनात्मक पूर्णांकों a और b के लिए ऐसी अद्वितीय पूर्ण संख्याएँ q और r विद्यमान है कि a = bq + r है तथा
(A) 0 < r < b
(B) 0 < r < b
(C) 0 ≤ r < b
(D) 0 ≤ r ≤ b
हल :
सही विकल्प (C) है।

प्रश्न 15.
संख्या n² – 1, 8 से विभाज्य होती है, यदि n है एक:
(A) पूर्णांक
(B) प्राकृत संख्या
(C) विषम संख्या
(D) सम संख्या
हल :
सही विकल्प (C) है।

प्रश्न 16.
यदि 65 और 117 के H.C.F. को 65m – 117 रूप में व्यक्त किया जा सके, तो m का मान है :
(A) 4
(B) 2
(C) 1
(D) 3

हल :
65 = 5 × 13
117 = 3 × 3 × 13
H.C.F. = 13
⇒ 65m – 117 = 13
[∵ H.C.F. = 65m – 117]
⇒ 65m = 13 + 117
⇒ 65m = 130
⇒ m = \(\frac{130}{65}\) = 2
अत: सही विकल्प (B) है।