JAC Class 10 Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

लघुत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
एक अर्धगोलाकार टैंक पानी से भरा है, जिसका पानी एक पाइप द्वारा \(\frac{25}{7}\) लीटर प्रति सेकण्ड की दर से खाली किया जा रहा है। ज्ञात कीजिए कि इस टैंक को आधा खाली करने में कितना समय लगेगा, यदि टैंक के आधार का व्यास 3 मी. है।
हल:
दिया है,
अर्धगोलाकार टैंक का व्यास = 3 मी
∴ अर्धगोलाकार टैंक की त्रिज्या (r) = \(\frac{3}{2}\) मी
अर्धगोलाकार टैंक का आयतन = \(\frac{2}{3}\) πr³

∵ \(\frac{25}{7}\) लीटर पानी को खाली करने में लगा समय
= 1 सेकण्ड
∴ \(\frac{99000}{28}\) लीटर पानी को खाली करने में लगा समय
= \(\frac{7}{25} \times \frac{99000}{28}\)
= 990 सेकण्ड
= \(\frac{990}{60}\) मिनट
= 16.5 मिनट
अतः आधे टैंक को खाली करने में लगा समय = 16.5 मिनट।

प्रश्न 2.
10 सेमी भुजा वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है ? इस प्रकार बने ठोस के संपूर्ण पृष्ठीय क्षेत्र को पेंट करवाने का ₹ 5 प्रति 100 वर्ग सेमी की दर से व्यय ज्ञात कीजिए। [π = 3.14 लीजिए]
हल:
अर्द्धगोले का अधिकतम व्यास:
= घन के एक किनारे की ल. (a) = 10 सेमी

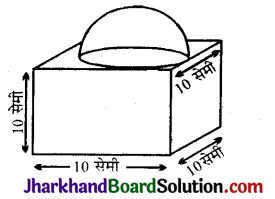
∴ अर्द्धगोले की त्रिज्या, r = \(\frac{10}{2}\) = 5 सेमी
अब ठोस का सम्पूर्ण पृष्ठीय क्षे. = घन का सम्पूर्ण पृष्ठीय क्षेत्रफल + अर्द्धगोलीय का वक्र पृष्ठीय क्षेत्रफल – अर्द्धगोले के आधार का क्षेत्रफल
= 6a² + 2πr² – πr²
= 6 × 10² + 2 × 3.14 × (5)² – 3.14 × (5)² सेमी²
= 600 + 157 – 78.5 cm²
= 678.5 cm²
पेंट करवाने का खर्चा = ₹ 5 प्रति 100 सेमी²
∴ ठोस को पेंट करवाने का खर्चा
= 678.5 × \(\frac{5}{100}\)
= ₹ 33.90 (लगभग)
अतः पेंट करवाने का व्यय = ₹ 33.90 (लगभग)।

प्रश्न 3.
एक ठोस धातु के बेलन के दोनों किनारों से उसी व्यास के अर्द्धगोले के रूप में धातु निकाली गई। बेलन की ऊँचाई 10 सेमी तथा इसके आधार की त्रिज्या 4.2 सेमी है। शेष बेलन को पिघलाकर 1.4 सेमी मोटी बेलनाकार तार बनाई गई तार की लम्बाई ज्ञात कीजिए।
हल:
ठोस धातु के बेलन की ऊँचाई = 10 सेमी
ठोस धातु के बेलन की त्रिज्या = 4.2 सेमी
∴ सभी अर्द्धगोले की त्रिज्या = ठोस धातु के बेलन की त्रिज्या; r = 4.2 सेमी
अब शेष बचे हुए बेलन का आयतन = बेलन का आयतन – 2 × अर्द्धगोले का आयतन
= πr²h – 2 × \(\frac{2}{3}\)πr³
= πr²\(\left(h-\frac{4}{3} r\right)\) = π × (4.2)² \(\left(10-\frac{4}{3} \times 4.2\right)\)
= π(4.2)² × 4.4 सेमी³
बेलनाकार तार की मोटाई = 1.4 सेमी
बेलनाकार तार की त्रिज्या = \(\frac{2}{3}\) = 7 सेमी
माना तार की लम्बाई = H सेमी
प्रश्नानुसार-
बेलनाकार तार का आयतन = शेष बचे हुए बेलन का आयतन
⇒ π × .7 × .7 × H = π × (4.2)².4.4
⇒ H = \(\frac{4.2 \times 4.2 \times 4.4}{.7 \times .7}\)
= 158.4
अतः तार की लम्बाई = 138.4 सेमी

प्रश्न 4.
पानी से भरी हुई अर्द्धगोलाकार टंकी को एक पाइप द्वारा 5 लीटर प्रति सेकण्ड की दर से खाली किया जाता है। यदि टंकी का व्यास 3.5 मीटर है तो कितने समय में आधी खाली हो जायेगी।
हल:
दिया है,
अर्द्धगोलाकार टैंकी का व्यास = 13.5 मीटर
∴ त्रिज्या r = \(\frac{3.5}{2}\) मीटर
अर्द्धगोलाकार टंकी की आयतन

…….5 लीटर पानी को खाली करने में लगा समय = 1 सेकण्ड
∴ \(\frac{67375}{21}\) लीटर पानी को खाली करने में लगा समय
= \(\left(\frac{1}{5} \times \frac{67375}{21}\right)\)
\(\left(\frac{1}{5} \times \frac{67375}{21}\right)\) से. = 641.66 से. = 10.69 मिनट
अतः आधी टंकी को खाली करने में लगभग = 10.69 मिनट।

प्रश्न 5.
आकृति में, PQRS एक वर्गाकार लॉन है जिसकी भुजा PQ = 42 मीटर है। दो वृत्ताकार फूलों की क्यारियाँ भुजा PS तथा QR पर हैं जिनका केन्द्र इस वर्ग के विकणों का प्रतिच्छेन बिन्दु O है। दोनों फूलों की क्यारियों (छायांकित भाग) का कुल क्षेत्रफल ज्ञात कीजिए।

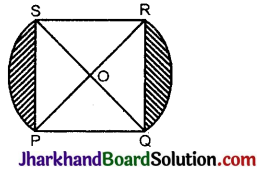
हल:
वर्गाकार लॉन का क्षेत्रफल PQRS = 42 मी × 42 मी
माना OP = OS = x मी
इसलिए x² + x² = (42)²
⇒ 2x² = 42 × 42
x² = 21 × 42 …..(1)
अब भाग POS का क्षेत्रफल = \(\frac{90}{360}\) πx² = \(\frac{1}{4}\) πx²
= \(\frac{1}{4} \times \frac{22}{7}\) × 21 × 42 मी² …..(2)
पुन: ΔPOS का क्षे. = \(\frac{1}{4}\) × वर्गाकार लॉन PQRS का क्षे.
= \(\frac{1}{4}\) × 42 × 42 मी² …..(3)
∠POQ = 90°
∴ फूलों की क्यारियों PSP का क्षे. = खण्ड POS भाग का क्षे. – ΔPOS का क्षे.
= \(\frac{1}{4} \times \frac{22}{7}\) × 21 × 42 – \(\frac{1}{4}\) × 42 × 42
= 33 × 21 – 441 = 693 – 441 = 252
दोनों फूलों की क्यारियों का कुल = 2 × 252 = 504 मी²
अतः दोनों फूलों की क्यारियाँ का कुल क्षे. 504 मी² है।

प्रश्न 6.
3.5 सेमी व्यास तथा 3 सेमी ऊँचे 504 शंकुओं को पिघलाकर एक धात्विक गोला बनाया गया। गोले का व्यास ज्ञात कीजिए। अतः इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [π = \(\frac{22}{7}\) लीजिए]
हल:
शंकु का व्यास = 3.5 सेमी
(r) = \(\frac{3.5}{2}\) सेमी
ऊँचाई (h) = 3 सेमी
अब प्रत्येक शंकु का आयतन = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times\left(\frac{3.5}{2}\right)^2 \times 3\) = 9.625 सेमी³
∴ 504 शंकुओं का आयतन = 504 × 9.625 = 4851 सेमी³
माना धात्विक गोले की त्रिज्या = R
प्रश्नानुसार,
गोले का आयतन = 504 × (शंकु का आयतन)
\(\frac{4}{3}\) πR³ = 4851
R³ = \(\frac{4851 \times 3}{4 \times 3.14}\) = 1157.625
R = 10.5 सेमी
गोले का व्यास = 2R = 2 × 10.5 = 21 सेमी
∴ गोले का पृष्ठीय क्षेत्रफल = 4πR² = 4 × \(\frac{22}{7}\) × (10.5)²
= 1386 सेमी²

प्रश्न 7.
दो घनों, जिनमें से प्रत्येक का आयतन 27 सेमी³ है, तो संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:

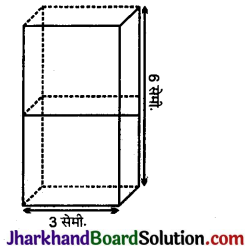
माना
धन की भुजा = a
घन का आयतन = 27 सेमी³
घन का आयतन = 27 भुजा³
27 सेमी³ = a³
a³ = 27
a = 3 सेमी
∴ घनाभ का सम्पूर्ण पृष्ठीय क्षे.
= 2 (ल. × चौ. + चौ. x ऊँ. + ऊँ. x ल.)
= 2 ( 3 × 3 + 3 × 6 + 6 × 3)
= 3(9 + 18 + 18)
= 3(45) = 135 सेमी²

प्रश्न 8.
एक ठोस अर्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल 462 वर्ग सेमी है। इसकी त्रिज्या ज्ञात कीजिए।
हल:
माना अर्धगोले की त्रिज्या r सेमी है।
प्रश्नानुसार,
अर्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल = 462 वर्ग सेमी
⇒ 3πR² = 462
⇒ 3 × \(\frac{22}{7}\) × r² = 462
⇒ r² = \(\frac{462 \times 7}{3 \times 22}\) = 49
⇒ r = \(\sqrt{49}\) = 7 सेमी
अतः अर्धगोले की त्रिज्या = 7 सेमी

प्रश्न 9.
एक चाँदी के घनाभ, जिसकी विमाएँ 8 सेमी × 9 सेमी × 11 सेमी है, को पिघलाकर समान त्रिज्या के सात गोले बनाए गए है। एक चाँदी के गोले की त्रिज्या ज्ञात कीजिए।
हल:
माना गोले की त्रिज्या = r सेमी
घनाभ का आयतन = लम्बाई × चौड़ाई × ऊँचाई
= 8 × 9 × 11 घन सेमी
∵ घनाभ को पिघलाकर सात गोले बनाए गए हैं,
∴ घनाभ का आयतन = 7 गोलों का आयतन
⇒ 8 × 9 × 11 = 7 × \(\frac{4}{3}\) πR³
⇒ 8 × 9 × 11 = \(7 \times \frac{4}{3} \times \frac{22}{7} \times r^3\)
⇒ r³ = \(\frac{8 \times 9 \times 11 \times 3}{4 \times 22}\) = 27
⇒ r³ = (3)³
⇒ r = 3 सेमी
अतः एक गोले की त्रिज्या = 3 सेमी

प्रश्न 10.
कोई बर्तन एक खोखले अर्धगोले के आकार का है। अर्धगोले का व्यास 14 सेमी है। इस बर्तन का आन्तरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है, अर्धगोले का व्यास = 14 सेमी
∴ त्रिज्या = 7 सेमी
∵ गोला खोखला है,
∴ अर्धगोले का आन्तरिक पृष्ठीय क्षेत्रफल = 2πr²
= 2 × \(\frac{22}{7}\) × (7)² वर्ग सेमी
= 308 वर्ग सेमी

प्रश्न 11.
7 मी व्यास वाला एक कुआँ खोदा जाता है और खोदने से निकली हुई मिट्टी को समान रूप से फैलाकर 22 मी × 14 मी × 2.5 मी वाला एक चबूतरा बनाया गया है। कुएं की गहराई ज्ञात कीजिए।
हल:
कुआँ बेलनाकार होता है।
माना कुएँ की गहराई h मी है।
∴ कुएँ से निकली मिट्टी का आयतन = बेलनाकार कुएँ का आयतन
= πr²h
= \(\frac{22}{7}\) × (7)² × घन मी
घनाभाकार चबूतरे का आयतन = 22 × 14 × 2.5 घन मी
प्रश्नानुसार,
\(\frac{22}{7}\) × (7)² × h = 22 × 14 × 2.5
⇒ h = \(\frac{22 \times 14 \times 2.5}{22 \times 7}\)
⇒ h = 17.5 मी
अतः कुएँ की गहराई = 17.5 मी

प्रश्न 12.
एक ठोस बेलन के आकार का है जिसके दोनों सिरे अर्धगोलाकार है। ठोस की कुल लम्बाई 20 सेमी है तथा बेलन का व्यास 7 सेमी है। ठोस का कुल आयतन ज्ञात कीजिए। (π = \(\frac{22}{7}\) प्रयोग कीजिए)
हल:
माना ABCD एक ठोस बेलन है जिसके दोनों सिरों पर दो एक-समान अर्धगोले हैं।

दिया है, पूरे ठोस की लम्बाई = 20 सेमी हैं, 2r = 7
∴ AB की लम्बाई = 20 – 2r
= 20 – 2 × \(\frac{7}{2}\)
h = 13 सेमी
अब, बेलन ABCD का आयतन = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 13\)
= 500.5 सेमी³
दोनों अर्धगोलों का आयतन = 2 × एक अर्धगोले का आयतन
= 2 × \(\frac{2}{3}\)πr³
= \(2 \times \frac{2}{3} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times \frac{7}{2}\)
= 179.67 सेमी³
ठोस का कुल आयतन = बेलन ABCD का आयतन + दोनों अर्धगोलों का आयतन
= 179.67 + 500.5
= 680.17 सेमी³

प्रश्न 13.
एक ही धातु के दो गोलों का भार 1 किलोग्राम तथा 7 किलोग्राम है। छोटे गोले की त्रिज्या 3 सेमी है। दोनों गोलों को पिघलाकर एक बड़ा गोला बनाया गया। नए गोले का व्यास ज्ञात कीजिए।
हल:
माना छोटे गोले की त्रिज्या r₁ तथा बड़े गोले की त्रिज्या r₂ है और माना इनसे मिलकर बनने वाले नए गोले की त्रिज्या R है।
छोटे गोले का आयतन = \(\frac{4}{3}\)πr₁³ [∵ r₁ = 3 ( दिया है)]
= \(\frac{4}{3}\)π(3)³ = 36π घन सेमी
अब,
छोटे गोले के पदार्थ का घनत्व = गोले का द्रव्यमान / गोले का आयतन
छोटे गोले के पदार्थ का आयतन = \(\frac{1}{36 \pi}\)
दोनों गोले एक ही पदार्थ से बने हैं, अतः इनके पदार्थ का घनत्व भी समान होगा।

अतः छोटे गोले का आयतन + बड़े गोले का आयतन = नए गोले का आयतन
⇒ \(\frac{4}{3} \pi r_1^3+\frac{4}{3} \pi r_2^3=\frac{4}{3} \pi R^3\)
⇒ r₁³ + r₂³ = R³
⇒ 27 + 189 = R³
⇒ R³ = 216
R = 6 ⇒ D = 12 सेमी
अतः नए गोले का व्यास 12 सेमी है।

प्रश्न 14.
त्रिज्या 6 सेमी और ऊँचाई 15 सेमी वाले एक लंबवृत्तीय बेलन के आकार का बर्तन आइसक्रीम से पूरा भरा हुआ है। इस आइसक्रीम को 10 बच्चों में बाँटने के लिए बराबर-बराबर शंकुओं में भरा जाना है, जिनका ऊपरी सिरा अर्धगोले के आकार का है। यदि शंक्वाकार भाग की ऊँचाई इसके आधार की त्रिज्या का 4 गुना है, तो आइसक्रीम शंकु की त्रिज्या ज्ञात कीजिए।
हल:
माना R तथा H क्रमशः लंबवृत्तीय बेलन की त्रिज्या तथा ऊँचाई है।
दिया है, R = 6 सेमी तथा H = 15 सेमी
लंब वृत्तीय बेलन में आइसक्रीम का आयतन
= πR²H
= π × 36 × 15
= 540π सेमी³
अब माना कि शंकु के आधार की त्रिज्या r सेमी हैं. तब इसकी ऊँचाई (h) = 4r

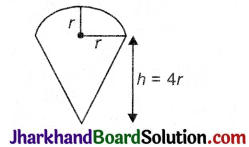
शंकु में आइसक्रीम का आयतन = शंकु का आयतन + अर्द्धगोले का आयतन
= \(\frac{1}{3}\)πr²h + \(\frac{2}{3}\)πr³
= \(\frac{1}{3}\)πr²(h + 2r)
= \(\frac{1}{3}\)πr²(4r + 2r) (∵ h = 4r)
= \(\frac{1}{3}\)πr² × 6r
= 2πr³
अब, 10 × शंकु में आइसक्रीम का आयतन = बेलन में आइसक्रीम का आयतन
⇒ 10 × 2πr³ = 540π
⇒ r³ = 27
⇒ r = 3 सेमी
अतः आइसक्रीम शंकु की त्रिज्या 3 सेमी है।

प्रश्न 15.
6 मी चौड़ी और 1.5 मी गहरी एक नहर में पानी 10 किमी/घंटा की चाल से बह रहा है। 30 मिनट में, यह नहर कितने क्षेत्रफल की सिंचाई कर पाएगी, जबकि सिंचाई के लिए 8 सेमी गहरे पानी की आवश्यकता होती है।
हल:
दिया है, नहर की चौड़ाई = 6 मी तथा गहराई 1.5 मी है व नहर में बहने वाले पानी की चाल 10 किमी/घंटा है, तो नहर में बहने वाला पानी घण्टे में 10 किमी या 10000 मी दूरी तय करेगा।
तथा माना सिंचाई हेतु क्षेत्रफल x मी है।
तब 30 मिनट में पानी का आयतन = 6 × 1.5 × 10000 × \(\frac{30}{60}\)
= 45000 मी³
अब, सिंचाई क्षेत्र का आयतन = नहर के पानी का आयतन
x × \(\frac{8}{100}\) = 45000
x = \(\frac{45000 \times 100}{8}\)
x = 562500 मी² या 56.25 हेक्टेयर

प्रश्न 16.
शंकु के छिन्नक के आकार की ऊपर से खुली एक बाल्डी का आयतन 12308.8 घन सेमी है। इसके ऊपरी तथा निचले वृत्तीय सिरों की त्रिज्याएँ क्रमशः 20 सेमी तथा 12 सेमी हैं। बाल्टी की ऊंचाई तथा इसके बनाने में लगी धातु की चादर का क्षेत्रफल ज्ञात कीजिए। [π = 1.732 लीजिए]
हल:
दिया है, r₁ = 20 सेमी, r₂ = 12 सेमी तथा छिन्नक का आयतन 12308.8 सेमी³ है।

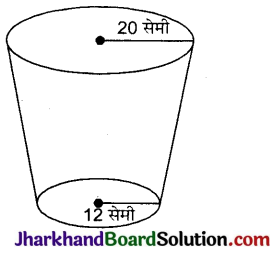
अब,
छिन्नक का आयतन = \(\frac{1}{3}\) × π × h (r₁² + r₂² + r₁r₂)
12308.8 = \(\frac{1}{3}\) × 3.14 × (20² + 12² + 20 × 12)
= \(\frac{1}{3}\) × 3.14 × h(400 + 144 + 240)
12308.8 = \(\frac{1}{3}\) × 3.14(784) × h
h = \(\frac{12308.8 \times 3}{3.14 \times 784}\)
h = 15 सेमी
धातु का क्षेत्रफल = πl(r₁ + r₃) + πr₂²
यहाँ l = \(\sqrt{\left(r_1-r_2\right)^2+h^2}\)
= \(\sqrt{(20-12)^2+15^2}\)
= \(\sqrt{289}\)
= 17 सेमी
धातु का क्षेत्रफल = 3.14 × 17 (20 + 12) + 3.14 × 12²
= 1708.16 + 452.16
= 2160.32 सेमी²

प्रश्न 17.
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्थ गोला खोद कर निकालते हुए, एक वस्तु बनाई गई, जैसा कि दी गई आकृति में दर्शाया गया है। यदि बेलन की ऊँचाई 10 सेमी है और आधार की त्रिज्या 3.5 सेमी है, तो इस वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

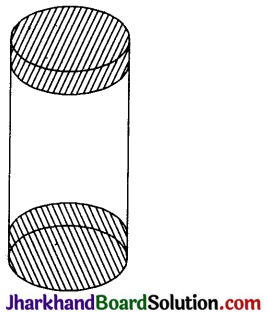
हल:
वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल = बेलन का वक्रपृष्ठीय क्षेत्रफल + 2 × अर्द्धगोले का वक्रपृष्ठीय क्षेत्रफल

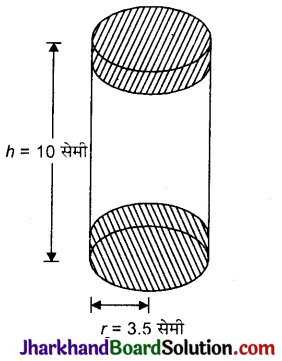
= 2πrh + 2 × 2πr²
= 2πr[h + 2r]
= 2 × \(\frac{22}{7} \times \frac{35}{10}\)[10 + 2 × 3.5]
= 22[17]
= 374 सेमी²

प्रश्न 18.
चावल की एक ढेरी शंकु के आकार की है जिसके आधार का व्यास 24 मी तथा ऊँचाई 3.5 मी है। चावलों का आयतन ज्ञात कीजिए इस ढेरी को पूरा-पूरा ढकने के लिए कितने कैनवस की आवश्यकता हैं?
हल:
शंक्वाकार ढेरी का व्यास = 24 मी
त्रिज्या, r = 12 मी
ऊँचाई, h = 35 मी
तिर्यक ऊँचाई, l = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(3.5)^2+(12)^2}\)
= \(\sqrt{12.25+144}\)
= \(\sqrt{156.25}\)
= 12.5 मी
चावलों का आयतन = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times(12)^2 \times(3.5)\)
= \(\frac{11}{3}\) × 144
= \(\frac{1584}{3}\)
= 528 मी³
ढेरी को ढकने के लिए कैनवास की आवश्यकता = शंकु का वक्रपृष्ठीय क्षेत्रफल
= πrl
= \(\frac{22}{7}\) × 12 × 12.5
= \(\frac{3300}{7}\)
= 471 \(\frac{3}{7}\) मी²

प्रश्न 19.
शंकु के छिन्नक के आकार की एक बाल्टी के निचले तथा ऊपरी किनारों के व्यास क्रमशः 10 सेमी तथा 30 सेमी हैं। यदि बाल्टी की ऊँचाई 24 सेमी है, तो ज्ञात कीजिए :
(i) बाल्टी को बनाने में लगने वाली धातु की शीट का क्षेत्रफल।
(ii) बाल्टी बनाने में सामान्य प्लास्टिक को क्यों नहीं लगाना चाहिए? [π = 3.14 लीजिए]
हल:
बाल्टी के ऊपरी सिरे का व्यास = 30 सेमी
बाल्टी के ऊपरी सिरे की त्रिज्या R = 15 सेमी
बाल्टी के निचले सिरे का व्यास = 10 सेमी
बाल्टी के निचले सिरे की त्रिज्या, r = 5 सेमी
बाल्टी की ऊँचाई, h = 24 सेमी
तिर्यक ऊँचाई, l = \(\sqrt{h^2+(R-r)^2}\)
= \(\sqrt{(24)^2+(15-5)^2}\)
= \(\sqrt{576+100}\)
= \(\sqrt{676}\)
= 26 सेमी

(i) बाल्टी बनाने में लगी धातु की शीट का क्षेत्रफल = छिन्नक का वक्रपृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल
= πl(R + r) + πr²
= π[l(R + r) + r²]
= 3.14[26(15 + 5) + 5²]
= 3.14[520 + 25]
= 3.44(545)
= 1711.3 सेमी²
(ii) बाल्टी बनाने में सामान्य प्लास्टिक इसलिए नहीं लगानीं चाहिये, क्योंकि उसकी शक्ति तथा गलनांक बहुत कम होता है और प्लास्टिक वातावरण के लिए हानिकारक है।

प्रश्न 20.
5.4 मी चौड़ी और 1.8 मी गहरी एक नहर में पानी 25 किमी / घण्टा की गति से बह रहा है। इससे 40 मिनट में कितने प्रतिशत क्षेत्रफल की सिंचाई हो सकती है, यदि सिंचाई के लिए 10 सेमी गहरे पानी की आवश्यकता है।
हल:
नहर की चौड़ाई = 5.4 मी
नहर की गहराई = 1.8 मी
नहर में 1 घण्टे में बहे पानी की लम्बाई = 25 किमी = 25000 मी
नहर में 1 घण्टे में बहे पानी का आयतन
= l × b × h
= 5.4 × 1.8 × 25000
= 243000 मी³
40 मिनट में पानी का आयतन = 243000 × \(\frac{40}{60}\)
= 162000 मी³
10 सेमी ऊँचाई के सींचे जाने वाले खेत का का क्षेत्रफल

= 162000 मी²
= 162 हेक्टेयर

प्रश्न 21.
एक शंकु के छिन्नक की तिर्यक ऊँचाई 4 सेमी है तथा इसके वृत्तीय सिरों की परिमाप 18 सेमी और 6 सेमी है। इस छिन्नक का व्रक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
छिन्नक को तिर्यक ऊँचाई = 4 सेमी
ऊपरी हिस्से का परिमाप = 18 सेमी
⇒ 2πR = 18 सेमी
⇒ R = \(\frac{9}{4}\) सेमी
निचले हिस्से का परिमाप = 6 सेमी
2πr = 6 ⇒ r = \(\frac{3}{8}\) सेमी
छिन्नक का वक्रपृष्ठ = πl[R + r]
= π × 4 × \(\left[\frac{9}{\pi}+\frac{3}{\pi}\right]\)
= π × 4 × \(\frac{12}{\pi}\) = 48 सेमी²

प्रश्न 22.
एक ठोस लोहे के घनाभ की विमाएँ 4.4 मी × 2.6 मी × 2.0 मी है। इसे पिघलाकर 30 सेमी आन्तरिक त्रिज्या और 5 सेमी मोटाई का एक खोखला बेलनाकार पाइप बनाया गया है। पाइप की लंबाई ज्ञात कीजिए।
हल:
पाइप की आन्तरिक त्रिज्या, r = 30 सेमी
पाइप की मोटाई = 5 सेमी
पाइप की बाहरी त्रिज्या = 30 + 5
R = 35 सेमी
माना, पाइप की लम्बाई = h सेमी
खोखले पाइप की आयतन = घनाभ की आयतन
πrh[R² – r²] = l × b × h
\(\frac{22}{7}\) × h[35² – 30²] = 4.4 × 2.6 × 1 × 100 × 100 × 100
\(\frac{22}{7}\) × h × 65 × 5 = 44 × 26 × 1 × 100 × 100
h = \(\frac{44 \times 26 \times 100 \times 100 \times 7}{22 \times 65 \times 5}\)
= 11200 सेमी
⇒ h = 112 मीटर

प्रश्न 23.
किसी वर्षा जल संग्रहण तन्त्र में, 22 मी × 20 मी की छत से वर्षा जल बहकर 2 मी आधार के व्यास तथा 3.5 मी ऊँचाई के एक बेलनाकार टैंक में आता है। यदि टैंक भर गया हो, तो ज्ञात कीजिए कि सेमी में कितनी वर्षा हुई। जल संरक्षण पर अपने विचार व्यक्त कीजिए।
हल:
एकत्रित पानी का आयतन = बेलनाकार टैंक का आयतन
L × B × H = πr²h
20 × 20× H = \(\frac{22}{7}\) × 1 × 1 × 3.5
22 × 20 × H = 11
H = \(\frac{11}{22 \times 20}=\frac{1}{40}\) मीटर
= \(\frac{1}{40} \times 100\)
= \(\frac{5}{2}\) = 2.5 सेमी
अतः 2.5 सेमी वर्षा हुई।
जल संरक्षण अति आवश्यक है, वह सूखे कि स्थिति के समय में कारगर सिद्ध होता है।

प्रश्न 24.
5 सेमी आंतरिक त्रिज्या तथा 24 सेमी ऊँचाई के एक शंक्वाकार बर्तन का \(\frac{3}{4}\) भाग पानी से भरा है। इस पानी को 10 सेमी आंतरिक त्रिज्या के बेलनाकार बर्तन में खाली किया जाता है। बेलनाकार बर्तन में पानी की ऊँचाई ज्ञात कीजिए।
हल:
प्रश्नानुसार,
शंक्वाकार बर्तन में \(\frac{3}{4}\) भाग का आयतन = बेलनाकार बर्तन का आयतन

अतः बेलनाकार बर्तन में पानी की ऊँचाई 1.5 सेमी है।

वस्तुनिष्ठ प्रश्न :

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क).
1. ऐसी वस्तुओं को जो स्थान घेरती हैं ………….. आकृतियाँ लाती हैं।
2. ठोस आकृति की सीमा बनाने वाली समतल आकृतियों का क्षेत्रफल ……………. क्षेत्रफल कहलाता है।
3. कोई वस्तु जितना स्थान घेरती है, उसे उस वस्तु का ……………… कहते है।
4. एक …………… के आयताकार समतल फलक होते हैं।
5. किसी आयत के उसकी एक स्थिर भुजा के परितः घुमाने से प्राप्त आकृति लम्बवृत्तीय ………….. कहलाती हैं।
उत्तर:
1. ठोस,
2. पृष्ठीय,
3. आयतन,
4. घनाभ,
5. बेलन।

निम्न में सत्य / असत्य बताइए :

प्रश्न (ख).
1. बेलन का आयतन 2πrh वर्ग इकाई होता है।
2. खोखले बेलन में लगे पदार्थ का आयतन दोनों बेलनों के आयतनों के योग के बराबर होता है।
3. गोले का आयतन 4πr² घन इकाई होता है।
4. अर्द्धगोले का सम्पूर्ण पृष्ठ = 3πr² वर्ग इकाई ।
5. शंकु का आयतन = πrl घन इकाई
उत्तर:
1. असत्य,
2. असत्य,
3. असत्य,
4. सत्य,
5. असत्य।

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
12π घन सेमी आयतन वाले गोले की त्रिज्या (सेमी में) है :
(A) 3
(B) 3\(\sqrt{3}\)
(C) 3^2/3
(D) 3^1/2
हल:
गोले का आयतन = \(\frac{4}{3}\)πr³
12π = \(\frac{4}{3}\)πr³
r³ = \(\frac{12 \pi \times 3}{4 \pi}\) = 9
r³ = 3²
⇒ r = 3^2/3
अत: सही विकल्प (C) है।

प्रश्न 2.
एक ठोस अर्धगोले का कुल पृष्ठीय क्षेत्रफल हैं:
(A) 3πr²
(B) 2πr²
(C) 4πr²
(D) \(\frac{2}{3}\)πr³
हल:
कुल पृष्ठीय क्षेत्रफल = 2πr² + πr² = 3πr²
अत: सही विकल्प (A) है।

प्रश्न 3.
एक 22 सेमी. आंतरिक किनारे वाले खोखले घन को 0.5 सेमी व्यास वाले गोलाकार कंचो से भरा जाता है तथा यह कल्पना की जाती है कि घन का भाग भरा नहीं जा सकता है। तब घन में समावेशित होने वाले कंचों की संख्या है :
(A) 142296
(B) 142396
(C) 142496
(D) 142596
हल:
दिया है,
घन की आन्तरिक भुजा = 22 सेमी.
तथा गोलाकार कंचे का व्यास = 0.5 सेमी.
∴ गोलाकार कंचे की त्रिज्या (r) = \(\frac{0.5}{2}\) सेमी.
= \(\left(\frac{5}{20}\right)\) सेमी.
∴ 1 गोलाकार कंचे का आयतन = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times\left(\frac{5}{20}\right)^3\)
= \(\frac{4}{3} \times \frac{22}{7} \times \frac{5 \times 5 \times 5}{20 \times 20 \times 20}\)
माना घन में समावेशित होने वाले कंचों की संख्या x है।
तब x कंचों का आयतन = \(x \times \frac{4}{3} \times \frac{22}{7} \times \frac{5 \times 5 \times 5}{20 \times 20 \times 20}\)
= \(\frac{x \times 55}{21 \times 40}\) घन सेमी. ……….(1)
घन का आन्तरिक आयतन = 22 × 22 × 22 घन सेमी.
……. खोखले घन को कंचों से भरा जाता है, तो पन का \(\frac{1}{8}\) भाग भरा नहीं जा सकता है।
∴ खोखले घन का कंचों से भरा गया भाग = 1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)
खोखले घन का कंचों से भरे भाग का आयतन = \(\frac{7}{8}\) × 22 × 22 × 22 घन सेमी. …..(2)
समीकरण (1) तथा (2) से
\(\frac{x \times 55}{21 \times 40}\) = \(\frac{7}{8}\) × 22 × 22 × 22
⇒ x = \(\frac{7 \times 22 \times 22 \times 22 \times 21 \times 40}{55 \times 8}\)
= 14 × 22 × 22 × 21 = 142296
अत: सही विकल्प (A) है।

प्रश्न 4.
यदि दो शंकुओं की त्रिज्याओं में अनुपात 3 : 1 और ऊँचाइयों में अनुपात 1 : 3 है, तो उनके आयतनों में अनुपात होगा :
(A) 2 : 1
(B) 3 : 1
(C) 1 : 3
(D) 1 : 2
हल:
माना दो शंकुओं की त्रिज्याएँ क्रमशः r₁ और r₂ ऊँचाइयाँ h₁ और h₂ हैं।
प्रश्नानुसार, \(\frac{r_1}{r_2}=\frac{3}{1}\) और \(\frac{h_1}{h_2}=\frac{1}{3}\)
दोनों शंकुओं के आयतनों का अनुपात

दोनों शंकुओं के आयतनों का अनुपात = 3 : 1
अत: सही विकल्प (B) है।

प्रश्न 5.
14 सेमी भुजा के एक घन से एक बड़े से बड़ा शंकु काटा जाता है। शंकु का आयतन है:
(A) 766.18 घन सेमी
(B) 817.54 घन सेमी
(C) 1232 घन सेमी
(D) 718.66 घन सेमी।

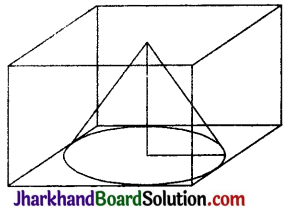
हल:
14 सेमी भुजा के घन से बड़े से बड़ा शंकु काटा जाता है।
अतः शंकु की ऊँचाई (h) = 14 सेमी
शंकु के आधार का व्यास = 14 सेमी
अत: शंकु के आधार की त्रिज्या = व्यास / 2 = \(\frac{14}{2}\)
= 7 सेमी
शंकु का आयतन = \(\frac{1}{3}\)πr²

अत: सही विकल्प (D) है।

प्रश्न 6.
दो गोलों के आयतनों का अनुपात 64 : 27 है। उनके पृष्ठीय क्षेत्रफलों का अनुपात है :
(A) 3 : 4
(B) 4 : 3
(C) 9 : 16
(D) 16 : 9
हल दिया है,
माना कि दो गोलों की त्रिज्याएँ क्रमशः r₁ तथा r₂ है। पहले गोले का आयतन : दूसरे गोले का आयतन = 64 : 27

अत: सही विकल्प (B) है।

प्रश्न 7.
क्रमशः आन्तरिक और बाहरी व्यास 4 सेमी और 8 सेमी वाले धातु के गोलाकार खोल को पिघलाकर आधार व्यास 8 सेमी. के एक शंकु के आकार में ढाला जाता है। इस शंकु की ऊँचाई है:
(A) 12 सेमी
(B) 14 सेमी
(C) 15 सेमी
(D) 18 सेमी
हल:
दिया है,
गोलाकार खोल की आन्तरिक व्यास = 4 सेमी
∴ गोलाकार खोल की आन्तरिक त्रिज्या
(r₁) = \(\frac{4}{2}\) = 2 सेमी
गोलाकार खोल की बाहरी व्यास = 8 सेमी
∴ गोलाकार खोल की बाहरी त्रिज्या
(r₂) = \(\frac{8}{2}\) = 4 सेमी
∴ शंकु का व्यास (r) = \(\frac{8}{2}\) = 4 सेमी
माना शंकु की ऊँचाई h सेमी है।
……. गोलाकार खोल को पिघलाकार शंकु के आकार में ढाला जाता है।
∴ गोलाकार खोल का आयतन = शंकु का आयतन
⇒ \(\frac{4}{3}\)π[r₂³ – r₁³] = \(\frac{1}{3}\)πr²h
⇒ 4[4³ – 2³] = 4² × h
⇒ 4 × [64 – 8] = 16 × h
⇒ 4 × 56 = 16 × h
⇒ h = \(\frac{4 \times 56}{16}\) = 14 सेमी
अत: सही विकल्प (B) है।

प्रश्न 8.
आधार व्यास 2 सेमी. और ऊँचाई 16 सेमी. वाले धातु के एक ठोस बेलन को पिघलाकर समान माप के बारह ठोस गोले बनाए जाते हैं। प्रत्येक गोले का व्यास है:
(a) 4 सेमी
(b) 3 सेमी
(c) 2 सेमी
(d) 6 सेमी
हल:
दिया है,
धातु के ठोस बेलन की ऊंचाई (h) = 16 सेमी
और धातु के ठोस बेलन का व्यास = 2 सेमी
∴ धातु के ठोस बेलन की त्रिज्या (r₁) = \(\frac{2}{2}\) = 1 सेमी
माना कि पिघलाकर समान माप के प्रत्येक ठोस गोले की त्रिज्या r₂ सेमी है।
….. ठोस बेलन को पिघलाकर समान माप के 12 ठोस गोले बनाए जाते हैं।
∴ ठोस बेलन का आयतन = 12 ठोस गोलों का आयतन
⇒ πr₁²h = 12 × \(\frac{4}{3}\)πr₂³
⇒ r₁²h = 16r₂³
⇒ 1² × 16 = 16r₂³
⇒ \(\frac{16}{16}\) = r₂³
⇒ r₂³ = 1 सेमी.
⇒ r₂ = \(\sqrt[3]{1}\) = 1 सेमी
∴ ठोस गोले का व्यास = 2 × 1 = 2 सेमी.
अंत: सही विकल्प (C) है।

प्रश्न 9.
यदि 11 सेमी × 3.5 सेमी × 2.4 सेमी मोम के एक घनाभ से 2.8 सेमी व्यास की एक मोमबत्ती बनाई जाती है। मोमबत्ती की लम्बाई होगी:
(A) 14 सेमी
(B) 15 सेमी
(C) 25 सेमी
(D) 12 सेमी
हल:
दिया है,
घनाभ की विमाएँ = 11 सेमी. × 3.5 सेमी × 2.4 सेमी.
∴ घनाभ का आयतन = 11 × 3.5 × 2.4
= 92.4 घन सेमी
माना मोमबत्ती की ऊँचाई h सेमी है।
मोमबत्ती का व्यास = 2.8 सेमी
मोमबत्ती की त्रिज्या (r) = \(\frac{2.8}{2}\) = 1.4 सेमी
प्रश्नानुसार,
मोमबत्ती का आयतन = घनाभ का आयतन
⇒ πr²h = 92.4
⇒ \(\frac{22}{7}\) × (1.4)² × h = 92.4
⇒ \(\frac{22}{7}\) × 1.4 × 14 × h = 92.4
⇒ h = \(\frac{92.4 \times 7}{22 \times 1.4 \times 1.4}\)
⇒ h = \(\frac{4.2}{0.2 \times 1.4}\) = 15 सेमी
मोमबत्ती की ऊँचाई = 15 सेमी
अत: सही विकल्प (B) है।

प्रश्न 10.
एक जलाशय लम्बवृत्तीय शंकु के छिन्नक के आकार में है। इसका ऊपरी सिरा 8 मीटर तथा पेंदी वाला सिरा 4 मीटर चौड़ा है। यदि यह 6 मीटर गहरा हो, तो इसकी क्षमता है:
(A) 176 मीटर³
(B) 196 मीटर³
(C) 200 मीटर³
(D) 110 मीटर³
हल:
दिया है,
छिन्नक के ऊपरी सिरे का व्यास = 8 मीटर
छिन्नक के ऊपरी सिरे की त्रिज्या (r₁) = \(\frac{8}{2}\) = 4 मीटर
छिन्नक के निचले सिरे का व्यास = 4 मीटर
छिन्नक के निचले सिरे की त्रिज्या (r₂) = \(\frac{4}{2}\) = 2 मीटर
छिन्नक की ऊँचाई (h) = 6 मीटर
छिन्नक का आयतन = \(\frac{1}{3}\)π × (r₁² + r₂² + r₁r₂)h
= \(\frac{1}{3} \times \frac{22}{7}\)(4² + 2² + 4 × 2) × 6
= \(\frac{22}{7}\) × (16 + 4 + 8) × 2
= \(\frac{22 \times 56}{7}\) = 22 × 8 = 176 घन मीटर
अत: सही विकल्प (A) है।

प्रश्न 11.
एक तेल की कुप्पी शंकु के छिन्नक को बेलन से जोड़ने पर बनी है। कुप्पी की ऊँचाई 12 सेमी है। बेलनाकार भाग की त्रिज्या 4 सेमी है और कुप्पी के. ऊपरी सिरे की त्रिज्या 9 सेमी है, तो शंकु के छिन्नक की तिर्यक ऊंचाई होगी:
(A) 13 सेमी
(B) 23 सेमी
(C) 26 सेमी
(D) 13.5 सेमी
हल:
कुप्पी के ऊपरी सिरे की त्रिज्या (r₁) = 9 सेमी
कुप्पी के निचले सिरे की त्रिज्या (r₂) = 4 सेमी
कुप्पी की ऊँचाई (h) = 12 सेमी
शंकु के छिनक की तिर्यक ऊँचाई (l) = \(\sqrt{h^2+\left(r_1-r_2\right)^2}\)
= \(\sqrt{(12)^2+(9-4)^2}\)
= \(\sqrt{(12)^2+(5)^2}\)
= \(\sqrt{144+25}\)
= \(\sqrt{169}\)
= 13 सेमी
अतः सही विकल्प (A) है।

प्रश्न 12.
9 सेमी त्रिज्या के धातु के गोले को पिघलाकर 3 सेमी त्रिज्या और 6 सेमी ऊँचाई के शंकु बनाये जा सकने वाले शंकुओं की संख्या है:
(A) 54
(B) 45
(C) 55
(D) 44
हल:
दिया है,
धातु के गोले की त्रिज्या (R) = 9 सेमी
शंकु की त्रिज्या (r) = 3 सेमी
तथा शंकु की ऊँचाई (h) = 6 सेमी
9 सेमी त्रिज्या वाले गोले का आयतन
\(\frac{4}{3}\)πR² = \(\frac{4}{3}\) × π × (9)²
= \(\frac{4}{3}\) × π × 9 × 9 × 9
= 4 × π × 3 × 81
= 972π घन सेमी
अब 3 सेमी त्रिज्या और 6 सेमी ऊँचाई वाले शंकु का आयतन
\(\frac{1}{3}\)πr²h = \(\frac{1}{3}\) × π × (3)² × 6
= \(\frac{1}{3}\) × π × 9 × 6
= π × 3 × 6 = 18π घन सेमी
गोले का आयतन शंकुओं की संख्या

अत: सही विकल्प (A) है।

प्रश्न 13.
एक ठोस लम्ब वृत्तीय शंकु को उसकी ऊँचाई के बीचों बीच से होकर जाते, शंकु के आधार के समान्तर एक तल द्वारा दो भागों में काटा गया है। इस प्रकार छोटे शंकु के आयतन का पूरे शंकु के आयतन से अनुपात है:
(A) 1 : 2
(B) 1 : 4
(C) 1 : 6
(D) 1 : 8
हल:
माना OAB एक शंकु है जिसकी ऊँचाई h तथा त्रिज्या R है। शंकु को बीचों बीच से आधार के समान्तर काटा गया है। अतः छोठे शंकु की ऊँचाई (h’) = \(\frac{h}{3}\)
माना कि छोटे शंकु की त्रिज्या r है।

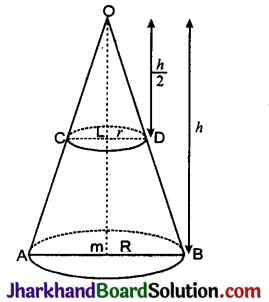
LD || MB
⇒ ∠OLD = ∠OMB (संगत कोण)
ΔOLD तथा ΔOMB में,
∠OLD = ∠OMB
∠LOD = ∠MOB (उभयनिष्ठ कोण)
ΔOLD ~ ΔOMB (AA समरूपता गुणधर्म से)
⇒ \(\frac{O L}{O M}=\frac{L D}{M B}\)
[समरूप त्रिभुजों की भुजाएँ समानुपाती होती हैं]
⇒ \(\frac{\frac{h}{2}}{h}=\frac{r}{R}\)
⇒ \(\frac{h}{2 h}=\frac{r}{R}\)
⇒ \(\frac{1}{2}=\frac{r}{R}\)
⇒ R = 2r
छोटे शंकु का आयतन : पूरे शंकु का आयतन
= πr²h’ : πR²h
= \(\frac{\pi \times r^2 \times \frac{h}{2}}{\pi \times(2 r)^2 \times h}\)
= \(\frac{r^2 \times h}{2 \times 4 r^2 \times h}=\frac{1}{8}\) = 1 : 8
अतः विकल्प (D) सही है।

प्रश्न 14.
तीनों घनों की कोर क्रमशः 3 सेमी, 4 सेमी और सेमी हैं। इनसे बनने वाले एक घन की भुजा है:
(A) 6 सेमी
(B) 5 सेमी
(C) 7 सेमी
(D) 4 सेमी
हल:
पहले घन का आयतन = (3)³ = 27 घन सेमी
दूसरे घन का आयतन = (4)³ = 64 घन सेमी
तीसरे घन का आयतन = (5)³ = 125 घन सेमी
इन तीनों घनों का कुल आयतन = 27 + 64 + 125
= 216 घन सेमी
∵ तीनों घनों से एक नया घन बनता है।
नये घन का आयतन = तीनों घनों का कुल आयतन
(भुजा)³ = 216
भुजा = \(\sqrt[3]{216}\)
= \(\sqrt[3]{6 \times 6 \times 6}\) = 6 सेमी
अतः सही विकल्प (A) है।

प्रश्न 15.
एक घनाभ की माप 18 सेमी × 12 सेमी × 9 सेमी है। इस घनाभ को पिघलाकार 3 सेमी भुजा वाले कितने घन बनाये जा सकते हैं ?
(A) 60
(B) 55
(C) 69
(D) 72
हल:
दिया है,
घनाभ की माप = 18 सेमी × 12 सेमी × 9 सेमी
दिये गये घनाभ का आयतन = 18 × 12 × 9
= 18 × 108
= 1944 घन सेमी
3 सेमी भुजा वाले घन का आयतन = (भुजा)³
= (3)³ = 27 घन सेमी
घनाभ को पिघलाकर बनाये गये घनों की संख्या = घनाभ का आयतन / 1 घन का आयतन
= \(\frac{1944}{27}\) = 72
अतः सही विकल्प (D) है।