JAC Class 10 Maths Important Questions Chapter 8 त्रिकोणमिति का परिचय

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 8 त्रिकोणमिति का परिचय Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 8 त्रिकोणमिति का परिचय

लघुत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
यदि tan A = \(\frac{3}{4}\) हो, तो sec A(1 – sin A)(sec A + tan A) का मान ज्ञात कीजिए।
हल:
दिया है कि
tan A = \(\frac{A B}{B C}=\frac{3}{4}\)

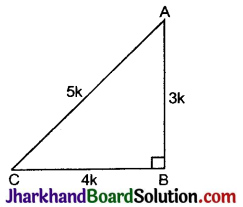
माना कि BC = 4k तथा AB = 3k
समकोण त्रिभुज ABC में,
पाइथागोरस प्रमेय से
AC² = AB² + BC²
= (3k)² + (4k)²
= 9k² + 16k²
= 25k²

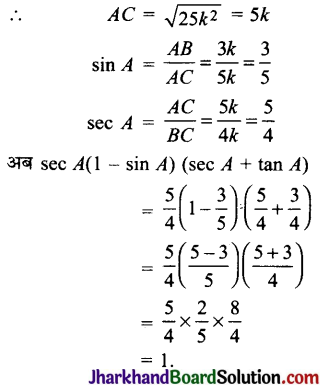
प्रश्न 2.
cos² 12° + cos² 78° का मान ज्ञात कीजिए।
हल:
cos² 12° + cos² 78°
cos² (90° – 78°) + cos² 78° = 0
[∵ cos (90° – θ) = sin θ]
sin² 78° + cos² 78° = 1.

प्रश्न 3.
मान ज्ञात कीजिए :
\(\frac{2 \cos 65^{\circ}}{\sin 25^{\circ}}-\frac{\tan 20^{\circ}}{\cot 70^{\circ}}-\sin 90^{\circ}\) + tan 5° tan 35° tan 60°.tan 55° tan 85°
हल:
\(\frac{2 \cos 65^{\circ}}{\sin 25^{\circ}}-\frac{\tan 20^{\circ}}{\cot 70^{\circ}}\) – sin 90° + tan 5° tan 35° tan 60°.tan 55° tan 85°
= \(\frac{2 \cos \left(90^{\circ}-25^{\circ}\right)}{\sin 25^{\circ}}-\frac{\tan \left(90^{\circ}-70^{\circ}\right)}{\cot 70^{\circ}}\) – 1 + tan (90° – 85°). tan 85° \(\sqrt{3}\).tan (90° – 55°) tan 55°
[∵ tan 60° = \(\sqrt{3}\) sin 90° = 1]
= \(\frac{2 \sin 25^{\circ}}{\sin 25^{\circ}}-\frac{\cot 70^{\circ}}{\cot 70^{\circ}}\) – 1 + cot 85° tan 85° \(\sqrt{3}\).cot 55°. tan 55°
[∵ cos (90° – θ) = sin θ, tan (90° – θ) = cot θ]
= 2 – 1 – 1 + \(\frac{1}{\tan 85^{\circ}}\).tan 85°\(\sqrt{3}\).\(\frac{1}{\tan 55^{\circ}}\)
= 1 × \(\sqrt{3}\) × 1
= \(\sqrt{3}\)
अत: \(\frac{2 \cos 65^{\circ}}{\sin 25^{\circ}}-\frac{\tan 20^{\circ}}{\cot 70^{\circ}}\) – sin 90° + tan 5° tan 35° tan 60°.tan 55°.tan 85° = \(\sqrt{3}\)

प्रश्न 4.
सिद्ध कीजिए कि :
\(\frac{\sin \theta}{1+\cos \theta}+\frac{1+\cos \theta}{\sin \theta}\) = 2 cosec θ.
हल:

= \(\frac{1+1+2 \cos \theta}{\sin \theta(1+\cos \theta)}=\frac{2+2 \cos \theta}{\sin \theta(1+\cos \theta)}\)
= \(\frac{2(1+\cos \theta)}{\sin \theta(1+\cos \theta)}=\frac{2}{\sin \theta}\)
= 2 cosec θ = R.H.S.
∴ L.H.S. = R.H.S.

प्रश्न 5.
यदि sin θ + cos θ = \(\sqrt{3}\), तब सिद्ध कीजिए कि tan θ + cot θ = 1.
हल:
दिया है,
sin θ + cos θ = \(\sqrt{3}\)
(sin θ + cos θ)² = (\(\sqrt{3}\))²
sin² θ + cos² θ + 2 sin θ cos θ = 3
⇒ 1 + 2 sin θ cos θ = 3
⇒ 2 sin θ cos θ = 3 – 1 = 2
⇒ 2 sin θ cos θ = \(\frac{2}{2}\) = 1
⇒ sin θ cos θ = sin² θ + cos² θ [∵ 1 = sin² θ + cos² θ]
⇒ \(\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin \theta \cos \theta}=1\)
⇒ \(\frac{\sin ^2 \theta}{\sin \theta \cos \theta}+\frac{\cos ^2 \theta}{\sin \theta \cos \theta}=1\)
⇒ \(\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\sin \theta}=1\)
⇒ tan θ + cot θ = 1.

प्रश्न 6.
यदि tan θ + sec θ, तब सिद्ध कीजिए कि sec θ = \(\frac{l^2+1}{2 l}\)
हल:
दिया है,
tan θ + sec θ = l

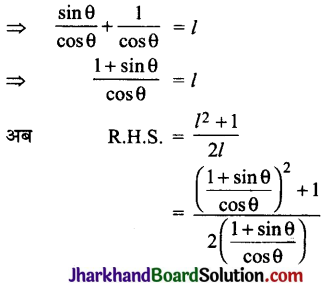
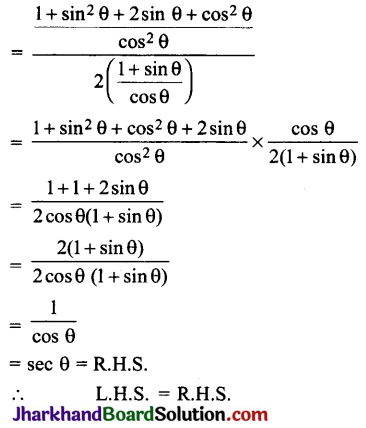
प्रश्न 7.
यदि 3 cot A = 4 तो \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) का मान ज्ञात कीजिए।
हल:
3 cot A = 4
cot A = \(\frac{4}{3}\)

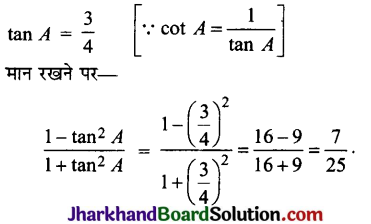
प्रश्न 8.
सिद्ध कीजिए कि :
tan⁴ θ + tan² θ = sec⁴ θ – sec² θ.
हल:
L.H.S. = tan⁴ θ + tan² θ
= tan2 θ + (tan2 θ + 1)
= (sec² θ – 1) (sec² θ – 1 + 1) [∵ tan² θ = sec² θ – 1]
= (sec² θ – 1) (sec² θ)
= sec⁴ θ – sec² θ
= R.H.S.
∴ L.H.S. = R.H.S.

प्रश्न 9.
यदि x = r sin A cos C, y = r sin A sin C तथा z = r cos A है, तो सिद्ध कीजिए कि x² + y² + z² = r² है।
हल:
दिया है,
x = r sin A cos C, y = sin A sin C तथा
z = r cos A
L.H.S. = x² + y² + z²
= (r sin A cos C)² + (r sin A sin C)² + (r cos A)²
= r² sin² A cos² C + r² sin² A sin² C + r² cos A
= r² sin² A (cos² C + sin² C) + r² cos² A
= r² sin² A + r² cos² A [∵ sin² C + cos² C = 1]
= r² (sin² A + cos² A)
= r²
R.H.S. = r²
∴ L.H.S. = R.H.S.

प्रश्न 10.
दिखाइये कि
tan 36° tan 17° tan 54° tan 73° = 1.
हल:
L.H.S. = tan 36° tan 17° tan 54° tan 73°
= tan (90° – 54°) tan (90° – 73°) tan 54° tan 73°
= cot 54° cot 73° tan 54° tan 73°
= 1 = R.H.S.

प्रश्न 11.
यदि cos A = \(\frac{12}{13}\), तो cot A का मान परिकलित कीजिए।
हल:
एक ΔABC की रचना करते हैं, जिसमें ∠B = 90° है।
दिया है, cos A = \(\frac{12}{13}\)
आधार / कर्ण = \(\frac{12}{13}\)
आधार = 12k
तथा कर्ण = 13k

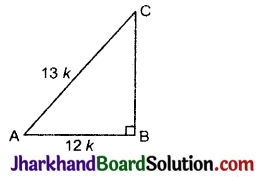
ΔABC में पाइथागोरस प्रमेय से
AC² = AB² + BC²
⇒ BC² = AC² – AB²
⇒ BC² = (13k)² – (12k)²
⇒ BC² = 169k² – 144k²
⇒ BC² = 25k²
⇒ BC ± 5k
cot A = आधार / लम्ब
= \(\frac{12 k}{5 k}\)
= \(\frac{12}{5}\)

प्रश्न 12.
त्रिकोणमितीय अनुपात tan A को sec A के पदों में लिखिए।
हल:
∵ sec² A = 1 + tan² A
⇒ tan² A = sec² A – 1
⇒ tan A = \(\sqrt{\sec ^2 A-1}\)

प्रश्न 13.
(i) यदि cos 3A = sin (A – 34°) हो, जहाँ A एक न्यूनकोण है तो A का मान ज्ञात कीजिए।
(ii) निम्नलिखित सर्वसमिका सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यूनकोण है।
\(\frac{1+\cot ^2 A}{1+\tan ^2 A}=\left(\frac{1-\cot A}{1-\tan A}\right)^2\)
हल:
(i) दिया है, cos 3A = sin(A – 34°)
⇒ cos 3A = cos[90° – (A – 34°)]
⇒ 3A = 90° – (A – 34°)
⇒ 3A = 90° – A + 34°
⇒ 4A = 124°
⇒ A = 31°

प्रश्न 14.
(i) (1 + tan θ + sec θ) ( 1 + cot θ – cosec θ) का मान ज्ञात कीजिए।
(ii) सिद्ध कीजिए: \(\frac{\tan A-\sin A}{\tan A+\sin A}=\frac{\sec A-1}{\sec A+1}\)
हल:
(i) (1 + tan θ + sec θ) ( 1 + cot θ – cosec θ)

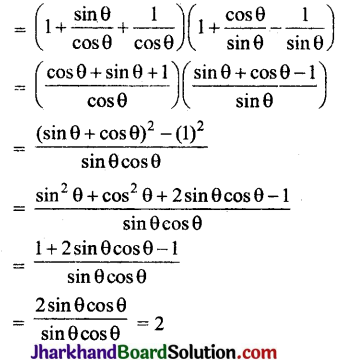
प्रश्न 15.
सिद्ध कीजिए :
2(sin⁶ θ + cos⁶ θ) – 3(sin⁴ θ + cos⁴ θ) + 1 =0
हल:
L.H.S. = 2(sin⁶ θ + cos⁶ θ) – 3(sin⁴ θ + cos⁴ θ) + 1
= 2[(sin² θ)³ + (cos² θ)³] – 3(sin⁴ θ + cos⁴ θ) + 1
= 2[(sin² θ + cos² θ) {sin² θ)² + (cos² θ)² – sin² θ cos² θ}] – 3(sin⁴ θ + cos⁴ θ) + 1
[∵ a³ + b³ = (a + b)(a² + b² – ab)]
= 2[1·(sin⁴ θ + cos⁴ θ – sin² θ cos² θ] – 3(sin⁴ θ + cos⁴ θ) + 1
= 2 sin⁴ θ + 2 cos⁴ θ – 2 sin² θ cos² θ – 3sin⁴ θ – 3 cos⁴ θ + 1
= -sin⁴ θ – cos⁴ θ – 2 sin² θ cos² θ + 1
= -[sin⁴ θ + cos⁴ θ + 2 sin² θ cos² θ] + 1
= -[(sin² θ + cos² θ)²] + 1
= – [(1)²] + 1
= 1 + 1 = 0 = R.H.S.

प्रश्न 16.
सिद्ध कीजिए:

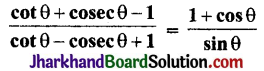
हल:

प्रश्न 17.
मान ज्ञात कीजिए :

हल:

प्रश्न 18.
सिद्ध कीजिए:

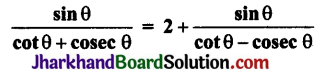
हल:


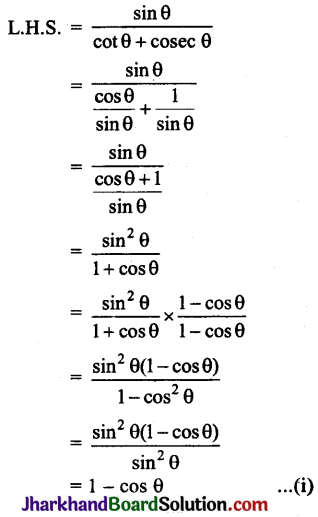
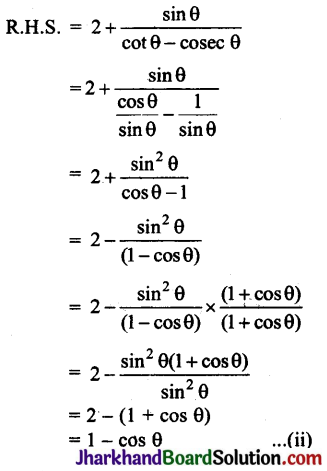
समीकरण (i) व (ii) से,
L.H.S. = R.H.S.

प्रश्न 19.
यदि sin (A + 2B) = \(\frac{\sqrt{3}}{2}\) तथा cos (A + 4B) = 0 है, जहाँ A तथा B न्यूनकोण हैं, तो A तथा B ज्ञात कीजिए।
हल:
दिया है,
sin(A + 2B) = \(\frac{\sqrt{3}}{2}\)
sin(A + 2B) = sin 60° (∵ sin 60° = \(\frac{\sqrt{3}}{2}\))
A + 2B = 60° …..(i)
तथा cos(A + 4B) = 0
cos(A + 4B) = cos 90° (∵ cos 90° = 0)
A + 4B = 90° ……(ii)
समीकरण (i) व (ii) को हल करने पर,
B = 15° तथा A = 30°

प्रश्न 20.
सिद्ध कीजिए :
\(\frac{\sin A-\cos A+1}{\sin A+\cos A-1}=\frac{1}{\sec A-\tan A}\)
हल:

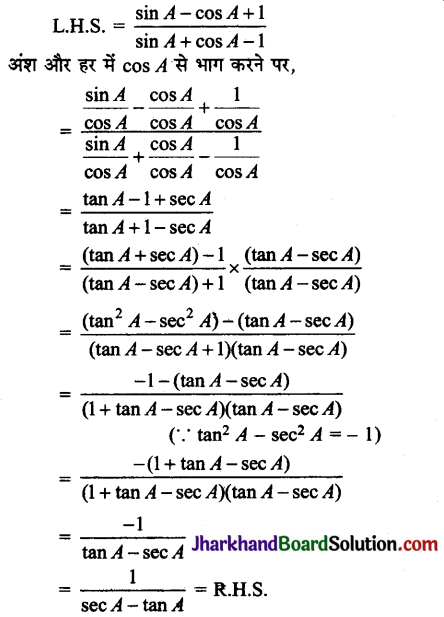
प्रश्न 21.
सिद्ध कीजिए:

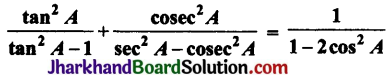
हल:

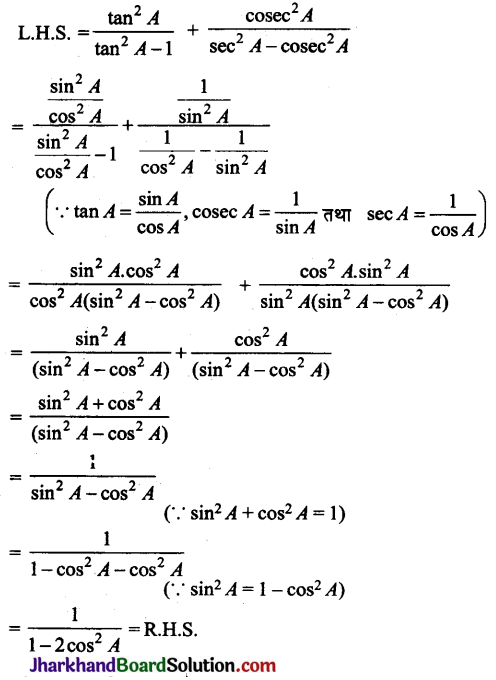
प्रश्न 22.
यदि sec θ = x + \(\frac{1}{4 x}\), x ≠ 0, तो (sec θ + tan θ) ज्ञात कीजिए :
हल:
sec θ = x + \(\frac{1}{4 x}\)
sec θ = \(\frac{4 x^2+1}{4 x}\)
दोनों पक्षों का वर्ग भरने पर प्राप्त होता है-

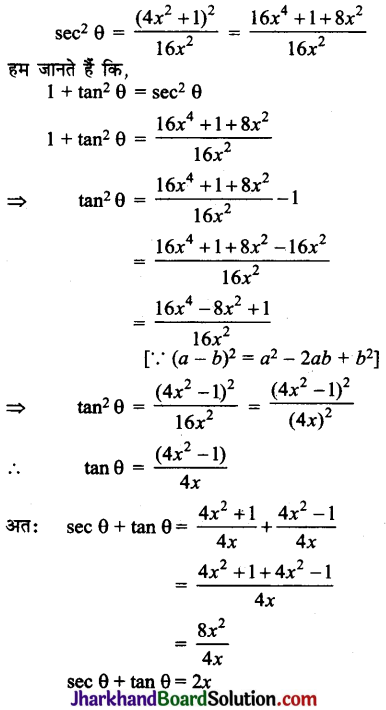
प्रश्न 23.
(1) यदि 4 tan θ = 3 है, तो \(\left(\frac{4 \sin \theta-\cos \theta+1}{4 \sin \theta+\cos \theta-1}\right)\) का मान ज्ञात कीजिए।
(ii) यदि tan 2A = cot (A – 18°), जहाँ 2A एक न्यून कोण है, तो A का मान ज्ञात कीजिए।
हल:
(i) यदि 4 tan θ = 3
tan θ = \(\frac{3}{4}\)
लम्ब = 3k; आधार = 4k; कर्ण = ?
पाइथागोरस प्रमेय से,
(कर्ण)² = (लम्ब)² + (आधार)²
= (3k)² + (4k)²
= 9k² + 16k²
= 25k²
कर्ण = 5k

(ii) यदि tan 2A = cot(A – 18°)
⇒ cot(90° – 2A) = cot(A – 18°)
⇒ 90° – 2A = A – 18°
-2A – A = – 18° – 90°
-3A = -108°
A = \(\frac{108^{\circ}}{3}\)
A = 36°.

प्रश्न 24.
सिद्ध कीजिए:
\(\frac{\sin A-2 \sin ^3 A}{2 \cos ^3 A-\cos A}\) = tan A.
हल:

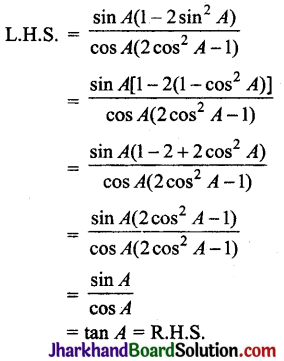
प्रश्न 25.
सिद्ध कीजिए:
\(\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}\) = sec θ – tan θ
हल:

प्रश्न 26.
सिद्ध कीजिए:
\(\frac{\tan ^2 \theta}{1+\tan ^2 \theta}+\frac{\cot ^2 \theta}{1+\cot ^2 \theta}=1\)
हल:

प्रश्न 27.
सिद्ध कीजिए : (1 + tan A – sec A) × (1 + tan A + sec A) = 2 tan A
हल:
L.H.S. = (1 + tan A – sec A) × (1 + tan A + sec A)
= {(1 + tan A) – sec A} {(1 + tan A) + sec A}
= (1 + tan A)² – sec² A
= 1 + tan² A + 2 tan A – sec² A
= sec² A + 2 tan A – sec² A
= 2 tan A = R.H.S.

प्रश्न 28.
सिद्ध कीजिए कि :

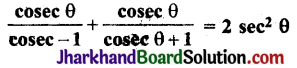
हल:

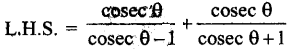
प्रश्न 29.
यदि x = 3 sin θ + 4 cos θ तथा y = 3 cos θ – 4 sin θ, तो ज्ञात कीजिए : x² + y² = 25
हल:
दिया है, x = 3 sin θ + 4 cos θ
x² = (3 sin θ + 4 cos θ)²
= 9 sin² θ + 16 cos² θ + 24 sin θ cos θ
तथा y = 3 cos θ – 4 sin θ
y² = (3 cos θ – 4 sin θ)²
= 9 cos² θ + 16 sin² θ – 24 sin θ cos θ
L.H.S. = x² + y²
= 9 sin² θ + 16 cos² θ + 24 sin θ cos θ + 9 cos² θ + 16 sin² θ – 24 sin θ cos θ
= 25 sin² θ + 25 cos² θ
= 25(sin² θ + cos² θ)
= 25 × 1 = 25 = R.H.S.

प्रश्न 30.
यदि sin θ + sin² θ = 1 है, तो सिद्ध कीजिए : cos² θ + cos⁴ θ = 1
हल:
दिया है,
sin θ + sin² θ = 1
⇒ sin θ = 1 – sin² θ
⇒ sin θ = cos² θ
अब cos² θ + cos⁴ θ = cos² θ + (cos² θ)²
= cos² θ + (sin θ)²
= cos² θ + sin² θ
= 1 = R.H.S.

वस्तुनिष्ठ प्रश्न :

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क).

1. \(\frac{\cos 80^{\circ}}{\sin 10^{\circ}}\) + cos 59° cosec 31° का मान …………… \frac{\cos 80^{\circ}}{\sin 10^{\circ}}है ।
2. \(\left(\sin ^2 \theta+\frac{1}{1+\tan ^2 \theta}\right)\) का मान ………………. है।
3. (1 + tan² θ) (1 – sin θ) (1 + sin θ) का मान ………………….. है।
4. sin 20° cos 70° + sin 70° cos 20° का मान है ……………….. ।
5. sin 65° + sin² 25° का मान है …………………… ।

उत्तर:

1. 2,
2. 1,
3. 1,
4. 1,
5. 1

निम्न में सत्य / असत्य बताइये :

प्रश्न (ख).

1. समकोण त्रिभुज में समकोण की सम्मुख भुजा को लंब कहते हैं।
2. sin व cos के मान सदैव 1 से कम या 1 के बराबर होते हैं।
3. cosee व sec के मान सदैव से अधिक या 1 के बराबर होते हैं।
4. यदि cot θ = \(\frac{12}{5}\) है, sin θ का मान \(\frac{13}{5}\) है।
5. tan² 60° + sin² 45° का मान \(\frac{7}{2}\) है।

उत्तर:

1. असत्य,
2. सत्य,
3. सत्य,
4. असत्य,
5. सत्य ।

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
यदि cos (10° + θ) = sin 30° है, तो θ का मान है:
(A) 50°
(B) 40°
(C) 80°
(D) 20°
हल:
cos (10° + θ) = sin 30°
cos(10° + θ) = sin(90° – 60°)
cos (10° + θ) = cos 60°
10° + θ = 60°
θ = 60° – 10° = 50
अत: सही विकल्प (A) है।

प्रश्न 2.
यदि sin A = cos A, 0 ≤ A ≤ 90° है, तो कोण A बराबर है:
(A) 30°
(B) 60°
(C) 0°
(D) 45°
हल:
sin A = cos A
⇒ sin A = sin (90° – A )
⇒ A = 90° – A
⇒ 2A = 90°
⇒ A = 45°
अतः सही विकल्प (D) है।

प्रश्न 3.
8 cot² A – 8 cosec² A बराबर है:
(A) 8
(B) 1
(C) – 8
(D) – \(\frac{1}{8}\)
हल:
8 cot² A – 8 cosec² A
= 8 cot² A – 8(1 + cot² A)
= 8 cot² A – 8 – 8 cot² A
= -8
अत: सही विकल्प (C) है।

प्रश्न 4.
यदि cos A = \(\frac{\sqrt{3}}{2}\), 0° < A < 90° है, तो A बराबर है:
(A) \(\frac{\sqrt{3}}{2}\)
(B) 30°
(C) 60°
(D) 1
हल :
cos A = \(\frac{\sqrt{3}}{2}\)
⇒ cos A = cos 30°
⇒ A = 30°
अतः सही विकल्प (B) है।

प्रश्न 5.
θ का ऐसा मान जिसके लिए sin (44° + θ) = cos 30° है, होना :
(A) 46°
(B) 60°
(C) 16
(D) 90°
हल:
sin(44° + θ) = cos 30°
⇒ sin(44° + θ) = cos(90° – 60°)
⇒ sin(44° + θ) = sin 60°
⇒ 44° + θ = 60°
⇒ θ = 60° – 44° = 16°
अत: सही विकल्प (C) है।

प्रश्न 6.
2 sin² 60° + 3 cot² 30° – tan 45° का मान होना :
(A) \(\frac{2}{19}\)
(B) \(\frac{12}{19}\)
(C) \(\frac{19}{2}\)
(D) इनमें से कोई नहीं।
हल:
2 sin² 60° + 3 cot² 30° – tan 45°
= 2 × \(\left(\frac{\sqrt{3}}{2}\right)^2\) + 3 × \((\sqrt{3})^2\) – 1
= 2 × \(\frac{3}{4}\) + 3 × 3 – 1
= \(\frac{3}{2}\) + 8 = \(\frac{19}{2}\)
अतः सही विकल्प (C) है।

प्रश्न 7.
यदि ΔABC का ∠C समकोण है, ता cos (∠A + ∠B) का मान है :
(A) 0
(B) 1
(C) \(\frac{1}{2}\)
(D) \(\frac{\sqrt{3}}{2}\)
हल:
दिया है, ΔABC का C समकोण है।

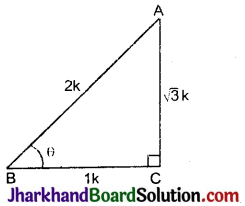
∵ हम जानते हैं कि त्रिभुज के तीनों कोणों का योग 180° होता है।
∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠B + 90° = 180°
⇒ ∠A + ∠B = 180° – 90°
⇒ ∠A + ∠B = 90°
दोनों तरफ cos लेने पर
⇒ cos (∠A + ∠B) = cos 90°
⇒ cos (∠A + ∠B) = 0
अत: विकल्प (A) सही है।

प्रश्न 8.
यदि sin A + sin² A = 1, तब व्यंजक (cos² A + cos² A) का मान हैं :
(A) 1
(B) \(\frac{1}{2}\)
(C) 2
(D) 3
हल:
दिया है,
sin A + sin² A = 1
⇒ sin A = 1 – sin² A
⇒ sin A = cos² A ……(1)
अब cos² A + cos⁴ A = cos² A + (cos² A)²
= cos² A + sin² A
= 1
[(1) का प्रयोग करने पर]
अत: विकल्प (A) सही है।

प्रश्न 9.
sin (45° + θ) – cos (45° – θ) बराबर है:
(A) 2 cos θ
(B) 0
(C) 2 sin θ
(D) 1
हल:
sin (45° + θ) – cos (45° – θ)
= sin (45° + θ) – cos [90° – (45° + θ)]
[∵ (45° – θ) = {90° – (45° + θ)}]
= sin (45° + θ) – sin (45° + θ)
[∵ cos (90° – θ) = sin θ = 0]
अतः विकल्प (B) सही है।

प्रश्न 10.
दिया गया है कि sin α = \(\frac{1}{2}\) और cos β = \(\frac{1}{2}\) तब (α + β) का मान है:
(A) 0°
(B) 30°
(C) 60°
(D) 90°
हल:
दिया है,
sin α = \(\frac{1}{2}\)
⇒ sin α = sin 30°
⇒ α = 30°
और cos β = \(\frac{1}{2}\)
⇒ cos β = cos 60°
⇒ β = 60°
अतः α + β = 30° + 60° = 90°
अतः विकल्प (D) सही है।

प्रश्न 11.
यदि sin θ – cos θ = θ तब (sin⁴ θ + cos⁴ θ) का मान है:
(A) 1
(B) \(\frac{3}{4}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{4}\)
हल:
दिया है,
sin θ – cos θ = 0 ⇒ sin θ = cos θ
⇒ \(\frac{\sin \theta}{\cos \theta}\) = 1 ⇒ tan θ = tan 45°
⇒ θ = 45°
अब sin⁴ θ + cos⁴ θ = sin⁴ 45° + cos⁴ 45°
= \(\left(\frac{1}{\sqrt{2}}\right)^4+\left(\frac{1}{\sqrt{2}}\right)^4\)
= \(\frac{1}{4}+\frac{1}{4}\)
= \(\frac{2}{4}\)
= \(\frac{1}{2}\)
अत: विकल्प (C) सही है।

प्रश्न 12.
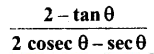बराबर है:
(A) tan θ
(B) cos θ
(C) sin θ
(D) cot θ.
हल:

अतः सही विकल्प (C)।

प्रश्न 13.
यदि sin θ = \(\frac{1}{2}\) हो, तो \(\frac{1-2 \sin ^2 \theta}{\sin \theta}\) का मान ज्ञात कीजिए ।
(A) 1
(B) 0
(C) 2
(D) – 1
हल:

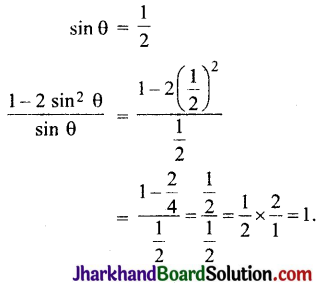
अतः विकल्प (A) सही है।

प्रश्न 14.
यदि sec θ + tan θ = 7 है, तो sec θ – tan θ बराबर है:
(A) \(\frac{1}{7}\)
(B) 7
(C) 6
(D) 49
हल:
∵ हम जानते हैं कि
sec² θ – tan² θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
⇒ 7 × (sec θ – tan θ) = 1
[दिया है : sec θ + tan θ = 7]
sec θ – tan θ = \(\frac{1}{7}\)
अतः विकल्प (A) सही है।

प्रश्न 15.
यदि 5 tan θ = 12 है, तो \(\frac{13 \sin \theta}{3}\) का मान है :
(A) 2
(B) 4
(C) 12
(D) 1
हल:
दिया है,
5 tan θ = 12
tan θ = \(\frac{12}{5}=\frac{A B}{B C}\)

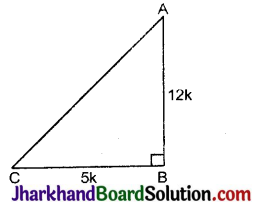
माना कि AB = 12k तथा BC = 5k
समकोण ΔABC में,
AC² = BC² + AB² (पाइथागोरस प्रमेय से)
⇒ AC² = (5k)² + (12k)²
⇒ AC² = 25k² + 144k²
⇒ AC² = 169k²
⇒ AC = \(\sqrt{169 k^2}\)
⇒ AC = 13k
∴ sin θ = \(\frac{A B}{A C}\)
= \(\frac{12 k}{13 k}=\frac{12}{13}\)
अब \(\frac{13 \sin \theta}{3}\)
= \(\frac{13 \times 12}{3 \times 13}\)
= 4
अतः विकल्प (B) सही है।