JAC Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल

Students should go through these JAC Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल

भूमिका :
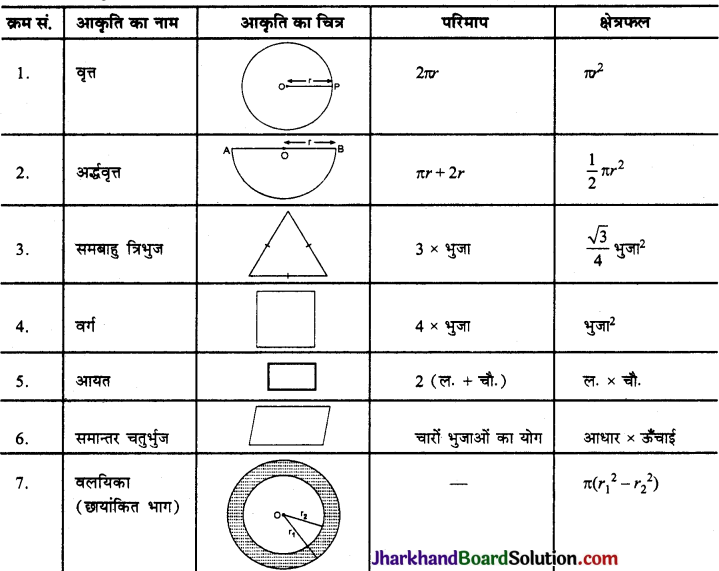
पिछली कक्षाओं में हमने समान्तर चतुर्भुअत : समचतुर्भुज तथा वर्ग के परिमाप तथा क्षेत्रफल के बारे में पढ़ा था। इस अध्याय में हम प्रारम्भ में वृत्त के परिमाप तथा क्षेत्रफल का पुनरावलोकन करेंगे तथा त्रिज्यखण्ड, वृत्तखण्ड का क्षेत्रफल ज्ञात करने के बारे में सीखेंगे। हम वृत्तों के भागों तथा वृत्तों से सम्बद्ध समतल आकृतियों के कुछ संयाजनों के क्षेत्रफलों के बारे में भी अध्ययन करेंगे।
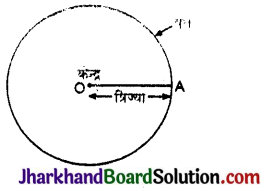
→ वृत्त (Circle) : वृत्त एक ऐसे बिन्दु का बिन्दु पथ है जो एक समतल में एक नियत बिन्दु से सदैव समान (अचर) दूरी पर गति करता है।
→ केन्द्र (Centre) : निश्चित बिन्दु को वृत्त का केन्द्र (O) कहते हैं।
→ त्रिज्या (Radius) : एक रेखाखण्ड जो वृत्त पर एक बिन्दु तथा इसके केन्द्र को जोड़ती है. त्रिज्या कहलाती है।
→ व्यास (Diameter) : केन्द्र से होकर गुजरने वाली जीवा जिसके अन्तः बिन्दु वृत्त पर होते हैं, वृत्त का व्यास कहलाता है।
व्यास = 2 × त्रिज्या
→ जीवा (Chord) : वृत्त पर दो बिन्दुओं को जोड़ने वाले रेखाखण्ड को वृत्त की जीवा कहते हैं।
→ चाप (Arc) : वृत्त पर दो बिन्दुओं के बीच की दूरी को वृत्त का चाप कहते हैं।
→ वृत्तीय क्षेत्र (Circular region) : वह क्षेत्र जिसमें सभी बिन्दु या तो वृत्त पर या वृत्त के अन्दर स्थित होते हैं वृत्तीय क्षेत्र कहलाता है।
→ अर्द्धवृत्तीय क्षेत्र (Semi circular region) : जब दो चाप बराबर होते हैं तब प्रत्येक एक अर्द्धवृत्त होता है तथा दोनों वृत्तखण्ड व त्रिज्यखण्ड बराबर होते हैं और प्रत्येक को अर्द्धवृत्तीय क्षेत्र से जाना जाता है।
→ संकेन्द्रीय वृत्त (Concentric Circles) : ऐसे दो या दो से ज्यादा वृत्त जिनका केन्द्र समान हो तथा त्रिज्याएँ विभिन्न हों, संकेन्द्रीय वृत्त कहलाते हैं।

वृत्त का परिमाप और क्षेत्रफल – एक समीक्षा
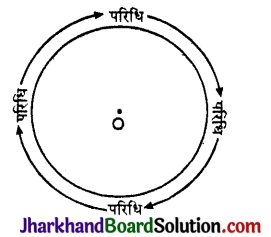
वृत्त की परिधि (Circumference of Circle) :
वृत्त का एक चक्कर लगाने पर तय की गई दूरी को वृत्त का परिमाप या परिधि कहते हैं। किसी भी वृत्त की परिधि और व्यास का अनुपात एक निश्चित अचर राशि होती है। इस अनुपात की अचर राशि को ग्रीक अक्षर π द्वारा प्रदिर्शित करते हैं।

अतः π = परिधि / व्यास
परिधि = π × व्यास
= π × 2 = 2πr
वृत्त की परिधि = 2πr
व्यवहार में π का मान प्रायः \(\frac{22}{7}\) अथवा 3.14 लिया जाता है परन्तु π एक अपरिमेय संख्या है जिससे इसका दशमलव अनावर्ती और असान्त है। आर्यभट्ट ने इसका मान 3.1416 ज्ञात किया था जो दशमलव के 4 स्थानों तक शुद्ध है।

वृत्त का क्षेत्रफल (Area of Circle) :

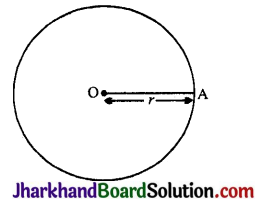
वृत्त का क्षेत्रफल = \(\frac{1}{2}\) × r × (वृत्त की परिधि)
= \(\frac{1}{2}\) × r × (2πr) = πr²
अतः वृत्त का क्षेत्रफल = π(त्रिज्या)²
वृत्त का व्यास वृत्त को दो समान भागों में विभाजित करता है। अतः
अर्द्धवृत्त का परिमाप = πr + 2r
अर्द्धवृत्त का क्षेत्रफल = \(\frac{1}{2}\)πr²

वलयिका का क्षेत्रफल (Area of an Annullus) :

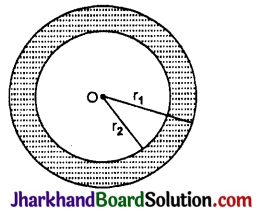
चित्र में, एक वलयिका का केन्द्र O है और जिसकी बाह्य और अन्तः त्रिज्याएँ क्रमशः r₁ और r₂ (r₁ > r₂) हैं।
वलयिका का क्षेत्रफल = दोनों वृत्तों के बीच का क्षेत्रफल
= बड़े वृत्त का क्षेत्रफल – छोटे वृत्त का क्षेत्रफल
= πr₁² – πr₂²
= π(r₁² – r₂²)
= π × (त्रिज्याओं के वर्गों का अन्तर)
अतः वलयिका का क्षेत्रफल = π(r₁² – r₂²)

त्रिज्यरखण्ड और वृत्तरखण्ड के क्षेत्रफल :
वृत्त के त्रिज्यखण्ड का क्षेत्रफल (Area of a Sector of a Circle) :
किसी भी वृत्त की दो त्रिज्याओं और एक चाप से घिरे हुए क्षेत्र को वृत्त का त्रिज्यखण्ड (Sector) कहते हैं।
चित्र में, वृत्त का एक त्रिज्यखण्ड AOB है। माना कि ∠AOB = θ है और θ < 180° जब कोण 6 का मान बढ़ता है तो चाप AB की लम्बाई भी उसी अनुपात में बढ़ती है। जब कोई चाप वृत्त के केन्द्र पर 180° का कोण अन्तरित करता है, तो

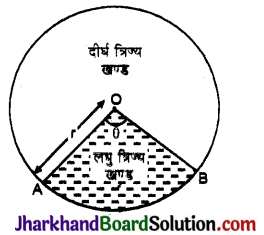
चाप की लम्बाई = अर्द्धवृत्त के चाप की लम्बाई
= πr
∵ केन्द्र पर 180° कोण अन्तरित करने वाले चाप की लम्बाई = πr
∴ केन्द्र पर θ कोण अन्तरित करने वाले चाप की लम्बाई = \(\frac{\pi r \theta}{180^{\circ}}=2 \pi r \times \frac{\theta}{360^{\circ}}\)
इसी प्रकार, जब कोई चाप वृत्त के केन्द्र पर 180° का कोण अन्तरित करता है, तो उसके संगत त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi r^2}{2}\)
∴ वृत्त के केन्द्र पर θ कोण अन्तरित करने पर बने त्रिज्यखण्ड का क्षेत्रफल
= \(\frac{\pi r^2 \theta}{2 \times 180^{\circ}}\)
= \(\frac{\pi r^2 \theta}{360^{\circ}}=\pi r^2 \times \frac{\theta}{360^{\circ}}\)
यदि r त्रिज्या के वृत्त में कोण θ के त्रिज्यखण्ड के चाप की लम्बाई L और क्षेत्रफल A है, तो
L = \(\frac{\pi r \theta}{180^{\circ}}=2 \pi r \times \frac{\theta}{360^{\circ}}\)
और A = \(\frac{\pi r^2 \theta}{360}=\pi r^2 \times \frac{\theta}{360^{\circ}}\)
चाप की लम्बाई (L) और त्रिज्यखण्ड के क्षेत्रफल (A) में सम्बन्ध :
A = \(\frac{1}{2}\)Lr
यहाँ कोण θ को डिग्री में लेते हैं।

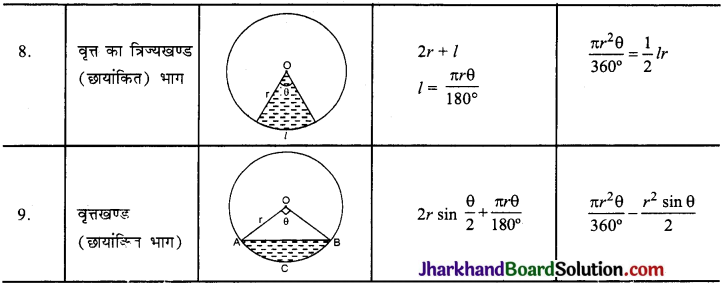
वृत्तखण्ड का क्षेत्रफल (Area of Segment of a Circle) :
वृत्त की प्रत्येक जीवा वृत्त को दो भागों में विभाजित करती है। इससे बने प्रत्येक भाग को वृत्तखण्ड कहते हैं। छोटे भाग को लघु वृत्तखण्ड तथा बड़े भाग को दीर्घ वृत्तखण्ड कहते हैं।
चित्र में, वृत्त का केन्द्र O हैं और इसकी त्रिज्या r है। जीवा PQ वृत्त को दो भागों में विभाजित करती है। हमें लघु वृत खण्ड PRQ का क्षेत्रफल ज्ञात करना है।

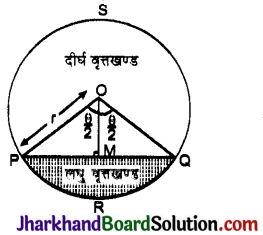
माना ∠POQ = θ
ΔΡΟΜ ≅ ΔQΟΜ (RHS सर्वांगसमता नियम से)
∠POM = ∠QOM = \(\frac{\theta}{2}\)
त्रिज्यखण्ड OPRQ का क्षेत्रफल = लघु वृत्तखण्ड PRQ का क्षेत्रफल + ΔPOQ का क्षेत्रफल
∴ लघु वृत्तखण्ड PRQ का क्षेत्रफल = त्रिज्यखण्ड OPRQ का क्षेत्रफल – ΔPOQ का क्षेत्रफल

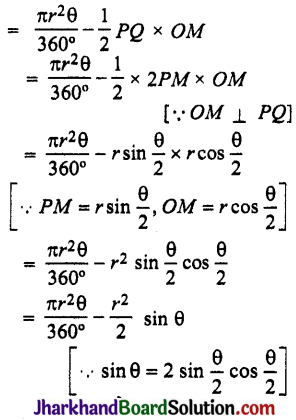
यदि हम दीर्घ वृत्तखण्ड का क्षेत्रफल ज्ञात करना चाहें, तो वृत्त के क्षेत्रफल में से लघु वृत्तखण्ड का क्षेत्रफल घटाकर ज्ञात कर सकते हैं।
अतः दीर्घ वृत्तखण्ड PSQ का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड PRQ का क्षेत्रफल
= πr² – \(\left[\frac{\pi r^2 \theta}{360^{\circ}}-\frac{r^2}{2} \sin \theta\right]\)
∴ दीर्घ वृत्तखण्ड PSQ का क्षेत्रफल = πr² – \(\frac{r^2}{2}\left[\frac{\pi \theta}{180^{\circ}}-\sin \theta\right]\)

समतल आकृतियों के संयोजन के क्षेत्रफल (Areas of Combinations of Plane Figures) :
समतल आकृतियों के छायांकित भाग का क्षेत्रफल ज्ञात करने के लिए निम्न सूत्रों की आवश्यकता होगी :