JAC Class 10 Maths Notes Chapter 14 सांख्यिकी

Students should go through these JAC Class 10 Maths Notes Chapter 14 सांख्यिकी will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 14 सांख्यिकी

भूमिका :
पिछली कक्षाओं में आपने विभिन्न आलेखों जैसे कि दंड आलेख, आयत चित्र, बारम्बारता बहुभुज के माध्यम से दिए हुए आँकड़ों को अवर्गीकृत एवम् वर्गीकृत बारम्बारता बंटनों में व्यवस्थित करना सीखा था तथा अवर्गीकृत आँकड़ों की केन्द्रीय प्रवृत्ति की मापें जैसे कि माध्य, माध्यक, बहुलक के बारे में भी अध्ययन किया था। इस अध्याय में हम वर्गीकृत आँकड़ों के माध्य, माध्यक और बहुलक कैसे ज्ञात किया जाता है सीखेंगे और संचयी बारम्बारता, संचयी बारम्बारता वक्रों, जो तोरण कहलाती है, को किस प्रकार खींचा जाता है, सीखेंगे।
→ सांख्यिकी (Statistics) : सांख्यिकी वह विज्ञान है, जिसमें आँकड़ों का संग्रह तथा वर्गीकरण किया जाता है तथा उनका विश्लेषण करके उनकी व्याख्या की जाती है।
सांख्यिकी को लैटिन शब्द ‘स्टेट्स (Status) या जर्मन शब्द स्टे (Statistic ) या इटेलियन शब्द स्टेटिस्टा (Statista) से लिया गया है।
→ प्रेक्षण (Observation) : सांख्यिकीय आँकड़ों का प्रत्येक पद प्रेक्षण कहलाता है।
→ बारम्बारता (Frequency) : किसी सारणी में किसी पद की बारम्बारता कई बार हो, तो वह पद जितनी बार आता है उसे पद की बारम्बारता कहते हैं।
→ बारम्बारता सारणी (Frequency table) : वर्ग अन्तराल के अनुसार वर्गीकरण करके जो सारणी बनती है उसे बारम्बारता सारणी कहते हैं।
→ वर्ग की सीमाएँ (Class limits) : वर्ग को निश्चित करने के लिए दो संख्याएँ प्रयोग की जाती हैं, जो उस वर्ग की सीमाएँ कहलाती हैं।
पहली संख्या वर्ग की निम्न सीमा तथा दूसरी संख्या वर्ग की उच्च सीमा कहलाती है।
→ वर्ग अन्तराल (Class size) : किसी वर्ग की उच्च सीमा तथा निम्न सीमा का अन्तर वर्ग अन्तराल कहलाता है।
→ वर्ग चिह्न (Class marks) : एक वर्ग अन्तराल का मध्य बिन्दु या वर्ग चिह्न उसकी उच्च और निम्न सीमाओं का औसत मान होता है।

→ संचयी बारम्बारता (Cumulative Frequency) : किसी वर्ग की संचयी बारम्बारता उस वर्ग तथा उस वर्ग तक के सभी वर्गों की बारम्बारताओं के योग बराबर होती है।
(i) समान्तर माध्य (Arithmetic Mean) : “वह मान है जो दिये हुए आँकड़ों के योगफल को, आँकड़ों की संख्या से भाग देने पर प्राप्त होता है।”
(ii) बहुलक (Mode) : सांख्यिकीय आँकड़ों में जिस पद की बारम्बारता सबसे अधिक होती है, बहुलक कहलाता है अथवा दिए गए आँकड़ों (प्रेक्षणों) में सबसे अधिक बार आने वाले आँकड़ों को बहुलक कहते हैं।
(iii) माध्यक (Median) : केन्द्रीय प्रवृत्ति का ऐसा मापक जो आँकड़ों में सबसे बीच के प्रेक्षण का मान देता है माध्यक कहलाता है।
केन्द्रीय प्रवृत्ति-“आँकड़ों में से किसी एक आँकड़े के पास जाने की उनकी प्रवृत्ति को केन्द्रीय प्रवृत्ति कहते हैं।”

1. प्राप्त आँकड़ों से समान्तर माध्य ज्ञात करना :
इस प्रकार यदि किसी चर राशि के n मान क्रमश: x₁, x₂, ……, x_n हों तो उनका
समान्तर माध्य = \(\frac{x_1+x_2+\ldots \ldots+x_n}{n}\) या \(\bar{x}=\frac{1}{n} \sum_{i=1}^n x_i\) [सूत्र रूप] …..(i)
प्रतीक : (i) Σ (सिग्मा) ग्रीक वर्णमाला का एक अक्षर है और गणित में इसको योग या संकलन (Summation) की प्रक्रिया दर्शाने के लिए प्रयोग में लाया जाता है।
\(\sum_{i=1}^n x_i=x_1+x_2+\ldots \ldots \ldots+x_n\)
(ii) \(\bar{x}\) [x bar] द्वारा समान्तर माध्य प्रकट किया जाता है।
(iii) समान्तर माध्य को संक्षेप में माध्य भी कहते हैं।

2. यदि आँकड़े बारम्बारता सारणी के रूप में दिए हों तो माध्य का अवकलन निम्न प्रकार किया जाता है:
(i) प्रत्यक्ष विधि (Direct Method)
(ii) कल्पित माध्य विधि (Assumed Mean Method) या संक्षेप विधि (Shortcut Method)
(iii) पद-विचलन विधि (Step-deviation Method)
अवर्गीकृत बारम्बारता बंटन से समान्तर माध्य :
क्रिया पद (Working Steps) :
पद I : प्रत्येक विचर को उसकी बारम्बारता से गुणा (f_i × x_i) कीजिए।
पद II : ऐसे सभी गुणनफलों का योगफल ज्ञात कीजिए।
पद III : उपर्युक्त योगफल में बारम्बारता के योगफल का भाग दीजिए।
पद IV : इस प्रकार प्राप्त भागफल समान्तर माध्य होगा।
प्रत्यक्ष विधि में निम्नलिखित सूत्र का प्रयोग किया जाता है:
माध्य = \(\bar{x}=\frac{\sum f_i x_i}{\sum f_i}\)

वर्गीकृत आँकड़ों का समान्तर माध्य :
क्रिया पद (Working Steps) :
पद I : वर्गीकृत बंटन में प्रत्येक वर्ग के मध्यमानों को ज्ञात कर उन्हें विचर x से प्रदर्शित कीजिए।

पद II : प्रत्येक वर्ग के मध्यमान को उसकी संगत बारम्बारता से गुणा कीजिए। (किसी वर्ग का मध्यमान उस वर्ग की निम्न एवं उच्च, दोनों सीमाओं के योगफल का आधा होता है।)
पद III : उपर्युक्त सभी गुणनफलों के योगफल में बारम्बारताओं के योगफल का भाग दीजिए।
पद IV : यह भागफल ही समान्तर माध्य होगा।
प्रत्यक्ष विधि में निम्नलिखित सूत्र का प्रयोग किया जाता है :
माध्य x \(\bar{x}=\frac{\sum f_i x_i}{\sum f_i}\)

कल्पित माध्य विधि (Assumed mean method) या संक्षेप विधि (Short-cut method) :
समान्तर माध्य (\(\bar{x}\)) = \(A+\frac{\sum f_i d_i}{\sum f_i}\)
जहाँ di = x_i – A, A = कल्पित माध्य
Σf_i = N = बारम्बारताओं का योग
नोट : सामान्यतः कल्पित माध्य विचर x का वह मान (अथवा मध्यमान) लिया जाता है जिसकी बारम्बारता अधिकतम हो। ऐसा करने से गणितीय परिकलन सरल हो जाता है।

पद-विचलन विधि (Step-deviation method) : इस विधि में विचलनों d_i = x_i – A के सभी मानों को किसी एक उभयनिष्ठ संख्या (माना h) से भाग देते हैं। ऐसी स्थिति में इन सभी विचलनों को h से विभाजित करते हुए नये विचलन \(u_i=\frac{x_i-A}{h}\) के रूप में लेते हैं।

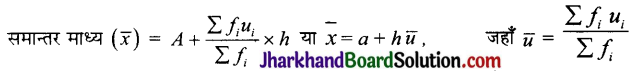
जहाँ \(u_i=\frac{x_i-A}{h}\)
A = कल्पित माध्य
h = वर्ग माप
Σf_i = N = बारम्बारताओं का योगे

वर्गीकृत आँकड़ों का बहुलक :
आँकड़ों के किसी संग्रह या संकलन में जिस प्रेक्षण की बारम्बारता (आवृत्ति) अधिकतम होती है, उस प्रेक्षण के मान को बहुलक कहते हैं।
जैसे: (i) एक कक्षा के 20 छात्रों की आयु वर्षों में निम्न प्रकार हैं, इसका बहुलक ज्ञात करना है :
15 16 13 14 14 13 15 14 13 13
14 12 15 14 16 13 14 14 13 15
उक्त बंटन से स्पष्ट है कि आयु 14 वर्ष सबसे अधिक 7 बार आया है। इसकी बारम्बारता सबसे अधिक है। अतः बहुलक 14 होगा।
(ii) कुछ विद्यार्थियों के प्राप्तांक निम्न प्रकार हैं, इनका बहुलक ज्ञात करना है :

हल: यहाँ प्राप्तांक 34 की बारम्बारता सबसे अधिक 20 है।
अतः बहुलक = 34 अंक होगा।

वर्गीकृत बारम्बारता बंटन से बहुलक :
(Mode from Grouped Frequency Distribution)
वर्गीकृत बारम्बारता बंटन से बहुलक निकालने के लिए अग्र क्रिया पद हैं:
पद I. वर्गीकृत बारम्बारता बंटन के जिस वर्ग की बारम्बारता सबसे अधिक होती है, उसे बहुलक वर्ग (modal class) कहते हैं। सर्वप्रथम बहुलक वर्ग को ज्ञात करते हैं।
पद II. बहुलक वर्ग के माध्यम से निम्न सूत्र का प्रयोग करते हुए बहुलक ज्ञात करते हैं:
बहुलक = \(l+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)
जहाँ l = बहुलक वर्ग की निम्न सीमा
f₁ = बहुलक वर्ग की बारम्बारता
f₀ = बहुलक वर्ग से ठीक पूर्व वर्ग की बारम्बारता
f₂ = बहुलक वर्ग के ठीक बाद के वर्ग की बारम्बारता
h = बहुलक वर्ग का अन्तराल

माध्यिका या माध्यक (Median) :
1. अवर्गीकृत या व्यक्तिगत श्रेणी से माध्यिका (Median from Ungrouped or Individual Series) : यदि किसी चर राशि x के मानों को आरोही (ascending) या अवरोही (descending) क्रम में रखा जाए, तो इस श्रेणी के मध्य (बीच) के पद को श्रेणी की माध्यिका या माध्यक (Median) कहते हैं।
(i) यदि पदों की संख्या विषम है, तो मध्य में एक ही पद \(\frac{n+1}{2}\) वाँ होगा।
माध्यक (M) = \(\frac{n+1}{2}\) वाँ होगा।
(ii) यदि पदों की संख्या सम है, तो

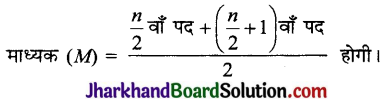
संचयी बारम्बारता बंटन का आलेखीय निरूपण (Graphical Representation of Cumulative Frequency) :
बारम्बारता बहुभुज तथा वक्र बनाने की दो विधियाँ हैं :
(1) ‘से कम’ विधि, (2) ‘से अधिक’ विधि।
(1) ‘से कम विधि’ (‘Less than’ method) : (i) वर्ग अन्तरालों की उच्च सीमा से प्रारम्भ करते हैं तथा वर्ग बारम्बारताओं को जोड़कर संचयी बारम्बारता (c.f.) बनाते हैं।
(ii) एक उचित पैमाना लेकर वर्गों की उच्च सीमा को X-अक्ष के अनुदिश निरूपित करते हैं।
(iii) एक उचित पैमाना लेकर संचयी बारम्बारताओं को Y-अक्ष के अनुदिश निरूपित करते हैं।
(iv) ग्राफ पर बिन्दुओं (x_i, f_i) को अंकित करते हैं, जहाँ x_i किसी वर्ग की उच्च सीमा तथा f_i संगत संचयी बारम्बारता है।
(v) चरण (iv) से प्राप्त बिन्दुओं को हाथ से वक्र के रूप में जोड़कर संचयी बारम्बारता वक्र अथवा तोरण प्राप्त करते है।

(2) से अधिक’ विधि (‘More than’ method) :
(i) वर्ग अन्तरालों की निम्न सीमा से प्रारम्भ करते हैं तथा बारम्बारताओं के योग में से प्रत्येक वर्ग की बारम्बारता घटाकर संचयी बारम्बारता बंटन प्राप्त करते हैं।
(ii) एक उचित पैमाना लेकर वर्गों की निम्न सीमा को X-अक्ष के अनुदिश निरूपित करते हैं।
(iii) एक उचित पैमाना लेकर संचयी बारम्बारताओं को Y-अक्ष के अनुदिश निरूपित करते हैं।
(iv) ग्राफ पर बिन्दुओं (x_i, f_i) को अंकित करते हैं, जहाँ x_i किसी वर्ग की निम्न सीमा तथा fi संगत संचयी बारम्बारता हैं।
(v) चरण (iv) से प्राप्त बिन्दुओं को हाथ से वक्र से रूप में जोड़कर बारम्बारता वक्र अथवा तोरण प्राप्त करते हैं।

तोरण अथवा वक्र द्वारा माध्यक ज्ञात करने की विधि : (i) ग्राफ पेपर पर दो प्रकार के बारम्बारता वक्रों में से एक खींचते हैं।
(ii) \(\frac{N}{2}\)(N = Σf_i) ज्ञात कर, Y-अक्ष पर संगत बिन्दु अंकित करते हैं।
(iii) इस संगत बिन्दु से X-अक्ष के समान्तर रेखा खींचते हैं जो वक्र को एक बिन्दु (माना P) पर काटती है।
(iv) यह बिन्दु P का भुज अर्थात् बिन्दु P का x-निर्देशांक माध्यिका होगी।