JAC Class 10 Maths Notes Chapter 2 बहुपद

Students should go through these JAC Class 10 Maths Notes Chapter 2 बहुपद will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 2 बहुपद

भूमिका :
पिछली कक्षाओं में हमने एक व्यंजक बहुपद तथा उनकी घातों, गुणनखंड तथा गुणक के बारे में पढ़ा है। स्मरण रहे कि P(x), x चर में एक बहुपद है P(x) में x की उच्चतम घात बहुपद की घात कहलाती है। उदाहरण के लिए, 4y² – 5y + 9, y चर में एक बहुपद है, जिसकी घात 2 है।
इस अध्याय में हम रैखिक तथा द्विघातीय बहुपदों के ज्यामितीय निरूपण (Geometrical Representation) और उनके शून्यकों के ज्यामितीय अर्थ के साथ-साथ बहुपद के गुणांकों और शून्यांकों के बीच सम्बन्धों का अध्ययन करेंगे।

बहुपद के प्रकार :
→ एकपदी (Monomial): ऐसे बहुपद को जिसमें केवल एक पद हो, एकपदी (monomial) कहते हैं:
जैसे : x², ax, 3x², a²x³, \(\frac{1}{2}\)x⁴ इत्यादि।

→ द्विपदी (Binomial): ऐसे बहुपद को जिसमें केवल दो पद हों, द्विपदी (binomial) कहते हैं; जैसे: ax + b, 5x² + 3x, a²xⁿ + b इत्यादि ।

→ त्रिपदी (Trinomial) ऐसे बहुपद को जिसमें केवल तीन पद हों, त्रिपदी (trinomial) कहते हैं: जैसे 3x² + 5x – 7, ax² + bx + c, ….. इत्यादि।

→ शून्य बहुपद (Zero polynomial): यदि किसी बहुपद में सभी पदों के गुणांक शून्य हों तो वह शून्य बहुपद कहलाता है। जैसे : p(x) = 0.
एक घात वाले बहुपद को रैखिक बहुपद, दो घात वाले बहुपद को द्विघात बहुपद और तीन घातों वाले बहुपद को त्रिघात बहुपद कहते हैं।

→ बहुपद की घात (Power of polynomial) चर x के बहुपद p(x) में x की उच्चतम घात को बहुपद की घात कहते हैं।
उदाहरण के लिए: (i) बहुपद p(x) = x⁵ + 4x³ – 3x² + 2x – 3 में चर राशि x की उच्चतम घात का पद है। जिसका घातांक 5 है। अतः बहुपद की घात 5 होगी।
(ii) बहुपद p(y) = 3y³ + 4y² – y + 8 में चर राशि की उच्चतम घात का पद 3y3 है, जिसका घातांक 3 है। अतः बहुपद P(y) की घात 3 होगी।

→ अचर बहुपद (Costant Polynomial): शून्य घात वाला बहुपद नियतांक या अचर बहुपद कहलाता है।
जैसे: p(x) = 7, g(x) = –\(\frac{3}{2}\), h(y) = 2, p(t) = 1 इत्यादि में किसी भी चर की घात शून्य होगी। अत: इस प्रकार के बहुपद अचर बहुपद कहलाते हैं।

→ रैखिक बहुपद (Linear Polynomial): घात 1 वाला बहुपद रैखिक बहुपद कहलाता है।
जैसे: 2x + 3, \(\sqrt{3}\)x + 5, y + \(\sqrt{2}\), x – \(\frac{2}{11}\), 3t + 4 इत्यादि सभी रैखिक बहुपद हैं।

→ द्विघात बहुपद (Quadratic Polynomial): घात 2 वाला बहुपद द्विघात बहुपद कहलाता है। द्विघात (Quadratic) शब्द क्वाड्रेट (quadrate) शब्द से बना है जिसका अर्थ वर्ग अर्थात् घात 2 है।
जैसे : f(x) = 2x² + 3x – \(\frac{4}{5}\), g(y) = 2y² – 3
h(u) = 2 – u² + \(\sqrt{3}\)u, p(v) = \(\sqrt{3}\)v² – \(\frac{4}{3}\)v + \(\frac{1}{2}\), इत्यादि द्विघात बहुपद हैं जिनके गुणांक वास्तविक संख्याएँ हैं।
व्यापक रूप से चर x में कोई द्विघात बहुपद f(x) = ax² + bx + c के रूप में होता है, जहाँ a, b, c वास्तविक संख्याएँ हैं, जहाँ a ≠ 0 है।

→ त्रिघात बहुपद (Cubic Polynomial) : घात 3 का बहुपद त्रिघात बहुपद कहलाता है।
जैसे : f(x)= \(\frac{9}{5}\)x³ – 2x² + \(\frac{7}{3}\)x – \(\frac{1}{5}\), g(x) = 2 – x³ तथा h(y) = 3y³ – 2y² + y + 1
चर x में एक त्रिघात बहुपद का व्यापक रूप निम्न है :
f(x) = ax³ + bx² + cx + d, जहाँ a, b, c, d वास्तविक संख्याएँ हैं जहाँ a ≠ 0 है।

बीजीय व्यंजक (Algebraic Expression) : कुछ निश्चित चर तथा अचर राशियों के योग, अन्तर, गुणन, भाग इत्यादि के संयोग से बने पद को बीजीय व्यंजक कहते हैं।
उदाहरणार्थ : f(x) = x³ – 6x² + x + 9, f(x) = -3x² + 2x – 1 तथा f(x) = 4x + 3 इत्यादि
इस प्रकार के बीजीय व्यंजकों को बहुपद (Polynomial) कहते हैं।
बहुपद : बीजीय व्यंजक के बहुपद होने के लिए निम्नलिखित शर्तें पूर्ण होनी चाहिए :
1. चर राशि का घातांक एक धनात्मक पूर्णांक हो।
2. पदों की संख्या निश्चित (सीमित) हो।
3. प्रत्येक पद में चर का गुणांक एक वास्तविक संख्या हो।
यदि x एक चर, प्राकृत संख्या और a₀, a₁, a₂, a₃, ….. a_n वास्तविक सख्याएँ हैं तो
p(x) = a₀ + a₁x + a₂x² + …… +a_nxⁿ
p(x) को चर x में एक बहुपद कहते हैं।
जहाँ a₀, a₁x, a₂x², a₃x³, …… इसके पद (Term) कहलाते हैं और a₀, a₁, a₂, a₃….. उनके गुणांक (Coefficient) कहलाते हैं।
उदाहरण के लिए:
(i) p(x) = 3x – 2 [चर x में एक बहुपद है।]
(ii) q(y) = 3y² – 2y + 4 [चर y मेँ एक बहुपद है।]
(iii) f(u) = \(\frac{1}{2}\)u³ – 3u² + 2u – 4 [चर u में एक बहुपद है।]
क्योंकि इन सभी (i), (ii) एवं (iii) की घात धनात्मक पूर्णांक है तथा प्रत्येक पद में चर राशि का गुणांक एक वास्तविक संख्या है।

निम्न व्यंजकों पर ध्यान दीजिए:
(i) p(x) = 2x² – 3\(\sqrt{x}\) यह बहुपद नहीं है क्योंकि \(\sqrt{x}\) या x^1/2 में x की घात \(\sqrt{2}\) है जो कि पूर्णांक नहीं है।
(ii) f(x) = \(\frac{1}{2 x^2-2 x+5}\) में भी x के घात धन पूर्णांक नहीं हैं अतः यह बहुपद नहीं है।
(iii) q(u) = x³ – \(\frac{1}{x^2}\) + 3 में \(\frac{1}{x^2}\) या x^-2 में x की घात -2 है, जो कि धन पूर्णाक नहीं है। अतः बहुपद नहीं है।

बहुपद का मान (Value of Poynomial): यदि f(x) चर x में एक बहुपद है और कोई वास्तविक संख्या है तो f(x) में x के स्थान पर α का मान रखने से प्राप्त वास्तविक संख्या बहुपद f(x) का x = α पर मान होगा और इसे f(α) द्वारा व्यक्त करते हैं।
जैसे: (i) f(x) = 2x² – 3x – 2 के x = 1 और x = -2 पर मान ज्ञात कीजिए ।
x = 1 पर, f(1) = 2(1)² – 3(1) – 2 = 2 × 1 – 3 × 1 – 2 = 2 – 3 – 2 = -3
x = -2 पर, f(-2) = 2(-2)² – 3(-2) – 2 = 2 × (+4) + 6 – 2 = 8 + 6 – 2 = 12
(ii) यदि बहुपद f(x) = x³ – 6x² + 11x – 6 है, x = -1 पर बहुपद का मान ज्ञात कीजिए।

बहुपद के शून्यक (Zeroes of Polynomial) : यदि किसी बहुपद p(x) में चर x के स्थान पर a (एक वास्तविक संख्या) प्रतिस्थापित करने पर p(a) = 0 हो, तो को बहुपद p(x) का शून्यक (Zero) कहते हैं। अर्थात् किसी भी बहुपद के शून्यकं ज्ञात करने का अर्थ होता है समीकरण p(x) = 0 को हल करना।
जैसे : (i) p(x) = 2x³ + 3x² + 3x + 2 का शून्यक ज्ञात करना है।
x = 0 पर, p(0) = 2(0)³ + 3(0)² + 3(0) +2
P(0) = 2 अर्थात p(0) ≠ 0
अत: शून्य, बहुपद p(x) का शून्यक नहीं है।
x = -1 पर, p(-1) = 2(-1)³ + 3(-1)² + 3(-1) + 2 = – 2 + 3 – 3 + 2 = 0
P(-1) = 0
अत: -1 बहुपद p(x) का एक शून्यक है।

विशेष :
(i) प्रत्येक रैखिक बहुपद का एक और केवल एक ही शून्यक होता है।
(ii) द्विघात बहुपद के दो शून्यक होते हैं।
(iii) त्रिघात बहुपद के तीन शून्यक होते हैं।
(iv) प्रत्येक बहुपद के वास्तविक शून्यक नहीं होते हैं।
जैसे : x² + a, x² + 2 तथा y² + y + 1 का कोई भी वास्तविक शून्यक नहीं है।
p(x) = x² + 6x + 15 का कोई शून्यक नहीं होता।
हल: माना कि p(x) = x² + 6x + 15
∴ p(x) = {x² + 2. (3). x + 9} + 6 = (x + 3)² + 6
यहाँ हम देखते हैं कि x के प्रत्येक वास्तविक मान के लिए (x + 3)² कभी भी ऋणात्मक मान ग्रहण नहीं कर सकता। अत: (x + 3)² का मान सदैव शून्य से बड़ा ही होगा। परिणामस्वरूप f(x) का मान भी 6 या उससे अधिक होगा।
इसलिए p(x) का कोई शून्यक विद्यमान नहीं है।

बहुपद के आलेख एवं शून्यकों का ज्यामितीय अर्थ :
बहुपद p(x) के ज्यामितीय आलेख को x अक्ष जिन बिन्दुओं पर प्रतिच्छेद करता है, उन बिन्दुओं के भुज या x-निर्देशांक बहुपद p(x) के शून्यक (zeroes) के रूप में जाने जाते हैं।
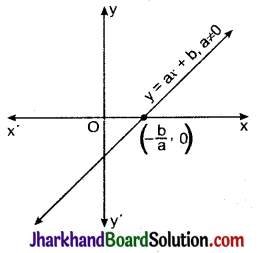
रैखिक बहुपद : व्यापक रूप में एक रैखिक बहुपद f(x) = ax + b, a ≠ 0 के लिए ग्राफ एक सरल रेखा प्राप्त होती है, जो x अक्ष को ठीक एक बिन्दु \(\left(-\frac{b}{a}, 0\right)\) पर काटती है।
अत: रैखिक बहुपद p(x) = ax + b, a ≠ 0 का केवल एक शून्यक होगा क्योंकि बहुपद का आलेख x-अक्ष पर केवल एक बिन्दु पर काटता है।

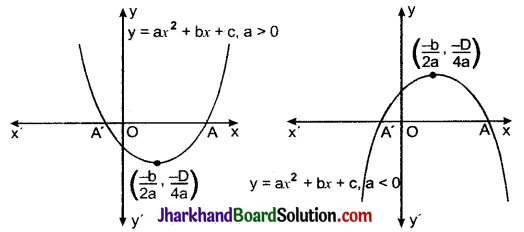
(ii) द्विघात बहुपद : किसी द्विघात समीकरण ax² + bx + c, a ≠ 0 के लिए ग्राफ दो में से किसी एक आकार का हो सकता है या तो ऊपर की ओर खुला (∪ की तरह) अथवा नीचे की ओर खुला (∩ की तरह) का होता है जो कि a > 0 या a < 0 पर निर्भर करता है।
इन वनों को परवलय (Parabola) कहते हैं।
बहुपद ax² + bx + c, जहाँ a ≠ 0 के शून्यक ठीक-ठीक उन बिन्दुओं के x-निर्देशांक होते हैं जहाँ बहुपद y = ax² + bx + c को निरूपित करने वाला ग्राफ (परवलय) x-अक्ष को प्रतिच्छेद करता है।
y = ax² + bx + c, के ग्राफ के आकार (परवलय) की तीन स्थितियाँ सम्भव हो सकती हैं।

स्थिति (I) : जब बहुपद ax² + bx + c के दो अलग-अलग गुणनखण्ड हैं:
इस स्थिति में ax² + bx + c का ग्राफ x-अक्ष को दो भिन्न-भिन्न बिन्दुओं A और A’ पर प्रतिच्छेद करता है तो इन बिन्दुओं के x निर्देशांक बहुपद ax² + bx + c के दो शून्यक होते हैं।
परवलय y = ax² + bx + c के शीर्ष के निर्देशांक \(\left(\frac{-b}{2 a}, \frac{-D}{4 a}\right)\) हैं, जहाँ D = b² – 4ac है।

किसी बहुपद के शून्यकों और गुणांकों में सम्बन्ध :
व्यापक रूप में, यदि द्विघात बहुपद p(x) = ax² + bx + c, जहाँ a ≠ 0 के शून्यक α और β हों, तो हम जानते हैं कि (x – α) और (x – β), p(x) के गुणनखण्ड होते हैं।
अतः ax² + bx + c = k(x – α) (x – β),
जहाँ k एक अचर है
= k[x² – (α + β)x + αβ]
ax² + bx + c = kx² – k(α + β)x + kαβ
दोनों पक्षों से x², x के गुणांकों तथा अचर पदों की तुलना करने पर,
a = k, b = – k (a + B) और c = kαβ
इससे प्राप्त होता है, α + β = \(\frac{-b}{a}\), αβ = \(\frac{c}{a}\)

व्यापक रूप में, यदि त्रिघात बहुपद ax³ + bx² + cx + d के शून्यक α, β और γ हों, तो हम जानते हैं कि (x – α), (x – β) और (x – γ) बहुपद के गुणनखण्ड होते हैं। अतः
ax³ + bx² + cx + d = k(x – α) (x – β) (x – γ), जहाँ k एक अचर है।
= k[{x² – (α + β)x + αβ} (x – γ)]
= k[x³ – (α + β + γ)x² + (αβ + βγ + γα)x – αβγ]
= kx³ – k(α + β + γ)x² + k (αβ + βγ + γλ) x – kλβγ
दोनों पक्षों से x³, x², x के गुणांकों और अचर पदों की तुलना करने पर,
a = k, b = -k(α + β + γ)
तथा c = k(αβ + βγ + γλ), d = -kαβγ
इससे प्राप्त होता है :

बहुपदों के लिए यूक्लिड की विभाजन एल्गोरिथ्म :
माना कि p(x) और g(x) कोई दो बहुपद हैं, जहाँ g(x) ≠ 0 हो तो बहुपद q(x) और r(x) ऐसे प्राप्त किए जा सकते हैं कि
p(x) = g(x) × q(x) + r(x)
जहाँ r(x) = 0 है अथवा r(x) की घात < g(x) की घात है।
उक्त परिणाम बहुपदों के लिए विभाजन एल्गोरिथ्म कहलाता है।