Students should go through these JAC Class 10 Maths Notes Chapter 4 द्विघात समीकरण will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 10 Maths Notes Chapter 4 द्विघात समीकरण
भूमिका :
द्विघात का शाब्दिक अर्थ वर्ग (square) है तथा द्विघातीय शब्द का आशय ‘वर्ग के समान’ से है। अतः वह समीकरण जिसमें अज्ञात राशि (चर) की उच्चतम घात (Index) 2 हो, द्विघात अथवा वर्ग समीकरण कहलाती है। जब हम द्विघात बहुपद को शून्य के तुल्य कर देते हैं, तो हमें द्विघात समीकरण प्राप्त होती है। जैसे- p(x) = ax2 + bx + c; a ≠ 0. एक द्विघात बहुपद है। यदि p(x) = 0 कर दें, तो ax2 + bx + c = 0; a ≠ 0 द्विघात समीकरण कहलाती है।
(1) द्विघात बहुपद (Quadratic Polynomial): वह बहुपद जिसकी घात 2 हो द्विघात बहुपद कहलाता है। द्विघात का व्यापक रूप ax2 + bx + c है। जहाँ a, b, c वास्तविक संख्याएँ हैं, a ≠ 0 तथा x एक चर है।
(2) समीकरण (Equation): किसी बहुपद को शून्य के बराबर करने से प्राप्त रैखिक व्यंजक को एक समीकरण कहते हैं। बराबर चिन्ह द्वारा इसे दो भागों में बाँटा जा सकता है। बायाँ पक्ष को L.H.S. तथा दायाँ पक्ष को R.H.S. कहते हैं।
उदाहरणार्थं- (i) x + 5 = 0 (रैखिक समीकरण)
बायाँ पक्ष = दायाँ पक्ष
(ii) 2y2 + 3y + 4 = 0 (द्विघात समीकरण)
(3) समीकरण के मूल (Roots of an equation): एक वास्तविक संख्या (a), समीकरण P(x) = 0 का एक मूल कहलाती है। यदि P(a) = 0 यदि P(x) = 0 एक द्विघात समीकरण हो, तो बहुपद P(x) के शून्यक समीकरण P(x) = 0 के मूल कहलाते हैं।
(4) काल्पनिक मूल (Imaginary roots ) : यदि किसी समीकरण के मूल वास्तविक संख्याएँ न हों तो उन्हें हम काल्पनिक मूल कहेंगे।
(5) चाल = दूरी / समय
(6) दूरी = चाल × समय
(7) समय = दूरी / चाल
![]()
द्विघात समीकरण (Quadratic Equation) :
दो घात की बहुपदीय समीकरण को द्विघात समीकरण कहते हैं व्यापक रूप में इसे इस प्रकार से व्यक्त किया जाता है, ax2 + bx + c = 0; जहाँ a, b, c वास्तविक संख्याएँ हैं तथा a≠ 0
व्यापक द्विघात समीकरण में x2 का गुणांक a, x का गुणांक b तथा c स्वतन्त्र अचर होता है।
3x2 + x – 2 = 0, x2 – 2x + 1 = 0; 4x2 + 4x + 1 = 0 आदि द्विघात समीकरण के कुछ उदाहरण हैं।
द्विघात समीकरण के मूल (Roots of a Quadratic Equation) : यदि संख्याएँ α और β द्विघात बहुपद ax2 + bx + c के शून्यक हों अर्थात् यदि संख्याएँ α तथा β द्विघात समीकरण ax2 + bx + c = 0 को सन्तुष्ट करती हों, तब c तथा द्विघात समीकरण ax2 + bx + c = 0 के मूल कहलाते हैं।
उदाहरण के लिए, द्विघाती बहुपद P(x) = x2 – x – 2 में
x = 2 रखने पर, P(2) = (2)2 – (2) – 2 = 4 – 2 – 2 = 4 – 4 = 0
x = – 1 रखने पर, P(-1) = (-1)2 – (-1) – 2 = 1 + 1 – 2 = 0
∴ 2 और -1 बहुपद के शून्यक हैं।
अतः 2 और -1 द्विघात समीकरण x2 – x – 2 = 0 के मूल कहलायेंगे।
टिप्पणी- (i) उपर्युक्त उदाहरण में 2 और -1 समीकरण x2 – x – 2 = 0 के मूल हैं, शून्यक नहीं।
(ii) शून्यर्कों का सम्बन्ध बहुपद से होता है जबकि मूलों का सम्बन्ध समीकरण से होता है।
द्विघात समीकरण को हल करने की विधियाँ :
द्विघात समीकरण को निम्नलिखित तीन विधियों द्वारा हल अर्थात् मूल ज्ञात किये जाते हैं-
(i) गुणनखण्ड विधि,
(ii) पूर्ण वर्ग बनाकर,
(iii) श्रीधर आचार्य सूत्र विधि द्वारा।
गुणनखण्ड विधि द्वारा द्विघात समीकरणों को हल करना :
(1) समीकरण को इस प्रकार व्यवस्थित करते हैं कि ‘=’ चिन्ह के दायीं ओर केवल शून्य तथा बाय और समीकरण के शेष सभी पद हों।
(2) बाई ओर के व्यंजक के रैखिक गुणनखण्ड प्राप्त करते हैं।
(3) अन्त में, प्रत्येक गुणनखण्ड को अलग-अलग शून्य के बराबर रखकर अज्ञात राशि के मान ज्ञात करते हैं जो समीकरण के अभीष्ट हल होते है।
![]()
पूर्ण वर्ग बनाकर द्विघात समीकरण का हल :
द्विघात समीकरण ax2 + bx + c = 0 को पूर्ण वर्ग बनाकर निम्नलिखित चरणों में हल किया जाता है:
(i) समीकरण में चर x सम्बन्धी सभी पदों को बाय ओर रखकर अचर पद को दायीं ओर रखते हैं।
(ii) x2 के गुणांक (यदि कोई हों) से दोनों पक्षों को भाग करते हैं ताकि x2 का गुणांक 1 (इकाई) बन जाए।
(iii) दोनों पक्षों में,
x के गुणांक के आधे का वर्ग अर्थात्  जोड़ने पर बायाँ पक्ष पूर्ण वर्ग बन जाएगा।
जोड़ने पर बायाँ पक्ष पूर्ण वर्ग बन जाएगा।
(iv) अन्त में दोनों पक्षों का वर्गमूल लेकर के मान ज्ञात करते हैं।
द्विघात समीकरण का श्रीधराचार्य विधि द्वारा हल :
हिन्दू गणितज्ञ श्रीधराचार्य ने द्विघात समीकरण ax2 + bx + c = 0, a ≠ 0 को पूर्ण वर्ग बनाने की विधि से हल ज्ञात करने के लिए मानक सूत्र दिया है। इसकी स्थापना एवं विवेचना आगे दी गई है।
माना समीकरण है : ax2 + bx + c = 0, a ≠ 0
⇒ x2 + \(\frac{b}{a}\)x + \(\frac{c}{a}\) = 0 (दोनों पक्षों में a का भाग देने पर)
⇒ x2 + \(\frac{b}{a}\)x = –\(\frac{c}{a}\)
अब x के गुणांक (\(\frac{b}{a}\)) के आधे (\(\frac{b}{2 a}\)) के वर्ग (\(\frac{b}{2 a}\))2 = \(\frac{b^2}{4 a^2}\) को समीकरण के दोनों पक्षों में जोड़ने पर,

श्रीधराचार्य सूत्र की निम्न प्रकार से व्याख्या की जा सकती है :
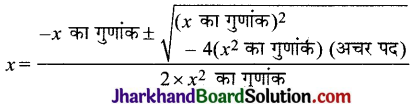
द्विघात समीकरण के मूल ज्ञात करने के इस सूत्र को द्विघाती सूत्र (Quadratic formula) कहते हैं।
![]()
मूलों की प्रकति :
विविक्तकर (Discriminant) राशि b2 – 4ac द्विघात समीकरण ax2 + bx + c = 0 की विविक्तकर कहलाती है। इसे संकेत Δ या D द्वारा व्यक्त किया गया है।
अत: D = b2 – 4ac;
जहाँ a, b, c वास्तविक संख्याएँ हैं।
द्विघात समीकरण के मूलों की प्रकृति : द्विघात समीकरण ax2 + bx + c = 0 के विविक्तकर D = b2 – 4ac के विभिन्न प्रकार के मानों के अनुरूप द्विघात समीकरण के मूलों की प्रकृति निम्न प्रकार प्रदर्शित की जा सकती है:
(i) यदि D = b2 – 4ac > 0 हो, तो समीकरण के मूल वास्तविक एवं पृथक्-पृथक् होंगे, अर्थात् यदि α और β दो मूल हों तो α = \(\frac{-b+\sqrt{b^2-4 a c}}{2 a}\)
तथा β = \(\frac{-b-\sqrt{b^2-4 a c}}{2 a}\)
(ii) यदि D = b2 – 4ac = 0 हो, तो समीकरण के मूल वास्तविक तथा समान होंगे अर्थात् α = \(-\frac{b}{2 a}\) = β
(iii) D = b2 – 4ac < 0 हो, तो समीकरण के कोई वास्तविक मूल नहीं होंगे अर्थात् दोनों मूल काल्पनिक होंगे।
अर्थात् द्विघात समीकरण ax2 + bx + c = 0; a ≠ 0 के मूलों की प्रकृति उसके विविक्तकर D = b2 – 4ac के मान पर निम्नवत् निर्भर करती है-
| विविक्तकर D = b2 – 4ac | मूलों की प्रकृति |
| धनात्मक तथा पूर्ण वर्ग | वास्तविक, परिमेय तथा भिन्न |
| धनात्मक (> 0) | वास्तविक, अपरिमेय तथा भिन्न |
| ऋणात्मक (< 0) | अधिकल्पित अर्थात् वास्तविक नहीं |
| शून्य (0) | वास्तविक परिमेय और समान |