JAC Class 10 Maths Notes Chapter 7 निर्देशांक ज्यामिति

Students should go through these JAC Class 10 Maths Notes Chapter 7 निर्देशांक ज्यामिति will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 7 निर्देशांक ज्यामिति

भूमिका :
किसी समतल में यदि किसी बिन्दु की स्थिति ज्ञात करनी हो तो दो संख्याओं की आवश्यकता पड़ती है। इन संख्याओं को बिन्दु के निर्देशांक कहते हैं। इससे सम्बन्धित ज्यामिति की शाखा को निर्देशांक ज्यामिति कहते हैं।

→ माना किसी समतल में दो परस्पर लम्बवत् रेखाएँ XOX’ और YOY’ हैं जो कि बिन्दु O पर प्रतिच्छेद करती हैं। इन्हें निर्देशांक अक्ष (Coordinate axes) कहते हैं और O को मूलबिन्दु (Origin) कहते हैं। XOX’ और YOY’ परस्पर लम्बवत् हैं। अत: XOX’ और YOY’ समकोणिक अक्ष या आयतीय निर्देशांक अक्ष (Rectangular axes) कहते हैं।

→ किसी बिन्दु की y-अक्ष से दूरी उस बिन्दु का x-निर्देशांक या भुज (abscissa) कहलाती है तथा उस बिन्दु की x अक्ष से दूरी उस बिन्दु का J-निर्देशांक या कोटि (ordinate) कहलाती है।
→ x- अक्ष पर स्थित किसी बिन्दु के निर्देशांक (x, 0) के रूप के होते हैं तथा y-अक्ष पर स्थित किसी बिन्दु के निर्देशांक (0, y) के रूप के होते हैं।
→ यदि हमें किसी बिन्दु के निर्देशांक ज्ञात हों तो उसका आलेख कागज पर अंकित कर सकते हैं जैसा कि हम अध्याय 2 में पढ़ चुके हैं कि y = ax² + bx + c (a ≠ 0) का आलेख एक परवलय (Parabola) होता है।
(1) निर्देशांक अक्ष (Coordinate Axes) : समतल पर किसी बिन्दु की स्थिति ज्ञात करने के लिए परस्पर दो लम्बवत् रेखाएँ खींची जाती हैं। जिसमें क्षैतिज रेखा को x-अक्ष तथा लम्बवत् रेखा को y-अक्ष कहते हैं। इन रेखाओं को निर्देशांक अक्ष कहते हैं।
(2) मूल बिन्दु (Origin): दो निर्देशांक अक्षों के प्रतिच्छेद बिन्दु को मूल बिन्दु कहते हैं। इसे सामान्यतः O से प्रदर्शित करते हैं।
(3) चतुर्थाश (Quadrants) : दो लम्बवत् निर्देशांक अक्षों द्वारा विभाजित चार भागों को चतुर्थांश कहते हैं।
(4) संरेखीय बिन्दु (Collinear points) : यदि तीन या तीन से ज्यादा बिन्दु एक सीधी रेखा पर स्थित हों तो उन्हें संरेखीय बिन्दु कहते हैं ।

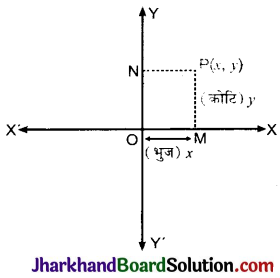
एक बिन्दु के कार्तीय निर्देशांक (Cartesian Co-ordinates ) : माना एक समतल में बिन्दु P के निर्देशांक ज्ञात करने के लिए बिन्दु P से XOX’ या x- अक्ष पर लम्बे PM और YOY या y-अक्ष पर लम्ब PN डालते हैं। मूल बिन्दु 0 से M की दिष्ट दूरी (OM x) बिन्दु P का x-निर्देशांक या भुज (abscissa) और M से P की दिष्ट दूरी (MP = y) बिन्दु P का y-निर्देशांक या कोटि (ordinate) कहलाता है। बिन्दु जिसका भुज और कोटि हो, बिन्दु (x, y) अर्थात् P(x, y) कहलाता है। बिन्दु के निर्देशांक सदैव क्रमित युग्म (x, y) में निरूपित किये जाते हैं अर्थात् बिन्दु के निर्देशांक लिखते समय x-निर्देशांक पहले और y-निर्देशांक बाद में लिखते हैं और इन्हें अल्प विराम () से अलग करते हुए छोटे कोष्ठक में लिखते हैं।

चतुर्थांश में निर्देशांकों के चिह्न (Sign of co-ordinates in quadrants) : दोनों अक्ष XOX’ और YOY’ समतल को चार भागों में विभाजित करते हैं। इन्हें चतुर्थांश कहते हैं XOY, YOX’, X’OY’ और Y’OX को क्रमशः प्रथम, द्वितीय, तृतीय और चतुर्थ चतुर्थांश कहते हैं। हम सदैव OX और OY दिशाओं को धनात्मक और OX’ और OY’ दिशाओं को ऋणात्मक लेते हैं।

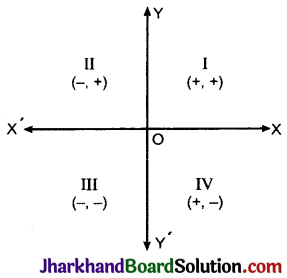
यदि समतल में किसी बिन्दु P के निर्देशांक (x, y) हों, तो
प्रथम चतुर्थांश में x > 0, y > 0; निर्देशांक (+, +)
द्वितीय चतुर्थाश में x < 0, y > 0; निर्देशांक (-, +)
तृतीय चतुर्थांश में x < 0, y < 0; निर्देशांक (-, -)
चतुर्थं चतुर्थांश में x > 0, y < 0; निर्देशांक (+, -)

दूरी सूत्र :
माना XOX’ और YOY’ निर्देशांक अक्ष हैं और समतल में स्थित दो बिन्दु P (x₁, y₁) और Q (x₂, y₂) हैं जिनके बीच की दूरी ज्ञात करनी है। बिन्दु P और Q से x- अक्ष पर लम्ब क्रमश: PM और ON डालते हैं और P से QN पर लम्ब PR डाला। अत: OM = बिन्दु P का भुज = x₁
इसी प्रकार :

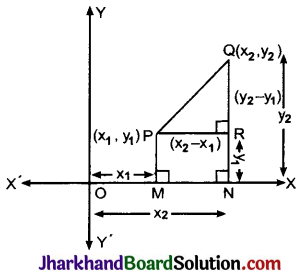
ON = x₂, PM = y₁ और QN = y₂
अत: चित्रानुसार, PR = MN = ON – OM = x₂ – x₁
और QR = QN – RN = QN – PM = y₂ – y₁
अतः समकोण त्रिभुत्र PRQ में पाइथागोरस प्रमेय से,
PQ² = PR² + QR²
या PQ² = (x₂ – x₁)² + (y₂ – y₁)²
या PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

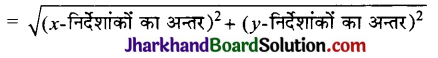
जो कि दो बिन्दुओं के बीच की दूरी का सूत्र है।
विशेष स्थिति : मूलबिन्दु O(0, 0) से किसी बिन्दु P(x, y) की दूरी OP = \(\sqrt{x^2+y^2}\)
ध्यान रखने योग्य बिन्दु :
→ x-अक्ष पर स्थित प्रत्येक बिन्दु की कोटि अर्थात् y-निर्देशांक = 0
→ y-अक्ष पर स्थित प्रत्येक बिन्दु का भुज अर्थात् x-निर्देशांक = 0
→ यदि किसी बिन्दु का भुज शून्य और कोटि धनात्मक है, तो वह बिन्दु धन y-अक्ष पर स्थित होगा।
→ यदि किसी बिन्दु का भुज शून्य और कोटि ऋणात्मक है, तो वह बिन्दु ऋण y-अक्ष पर स्थित होगा।
→ यदि किसी बिन्दु का भुज धनात्मक और कोटि शून्य है, तो वह बिन्दु धन x-अक्ष पर स्थित होगा।
→ यदि किसी बिन्दु का भुज ऋणात्मक और कोटि शून्य है, तो वह बिन्दु ऋण x-अक्ष पर स्थित होगा।

विभाजन सूत्र :
दो बिन्दुओं के मध्य दूरी का आन्तरिक और बाह्य विभाजन (Internal and external division of distance between two points) : माना समतल में दो बिन्दु A और B हैं। यदि रेखा AB पर कोई बिन्दु P, A व B के मध्य स्थित हो, तो इस प्रकार के विभाजन को आन्तरिक विभाजन कहते हैं। यदि विभाजन बिन्दु P, A और B के मध्य में नहीं होकर A के बायीं ओर या B के दायीं ओर स्थित हो, तो ऐसे विभाजन को बाह्य विभाजन कहते हैं।
(i) आन्तरिक विभाजन (Internal division ) : माना समतल में स्थित दो बिन्दु (x₁, y₁) और B(x₂, y₂) हैं और बिन्दु P (x, y) रेखाखण्ड AB को m₁ : m₂ में आन्तरिक रूप से विभाजित करता है बिन्दु A, P और B से x-अक्ष पर डाले गये लम्ब क्रमश: AL, PM और BN हैं। बिन्दु A से PM पर लम्ब AQ और बिन्दु P से BN पर लम्ब PR डाला, तब

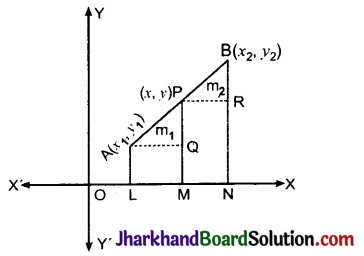
OL = x₁, OM = x, ON = x₂
AL = y₁, PM = y और BN = y₂
∴ AQ = LM = OM – OL = x – x₁
PR = MN = ON – OM = x₂ – x
PQ = PM – QM = PM – AL = y – y₁
BR = BN – RN = BN – PM = y₂ – y
चित्र में, त्रिभुज AQP और त्रिभुज PRB स्पष्टतः समरूप त्रिभुज हैं।

(ii) बाह्य विभाजन (External Division) : माना समतल में स्थित बिन्दु A(x₁, y₁) और B(x₂, y₂) हैं। बिन्दु P(x, y) रेखाखण्ड AB को m₁ : m₂ मैं बाह्य विभाजित करता है। बिन्दु A, B और P से x-अक्ष पर डाले गये लम्ब क्रमश: AL, BN और PM हैं। बिन्दु A से PM पर लम्ब AQ और B से PM पर लम्ब BR डाला, तब OL = x₁, ON = x₂, OM = x, AL = y₁, BN = y₂ और PM = y
∴ AQ = LM = OM – OL = x – x₁
BR = NM = OM – ON = x – x₂
PQ = PM – QM = PM – AL = y – y₁
और PR = PM – RM = PM – BN = y – y₂
चित्र में, त्रिभुज AQP और त्रिभुज BRP स्पष्टत: समरूप त्रिभुज हैं।


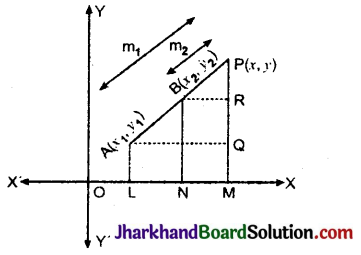
इसको विभाजन सूत्र (Section formula) कहा जाता है। इसी सूत्र को A. P और B से y-अक्ष पर लम्ब डालकर और ऊपर की भाँति प्रक्रिया अपनाकर भी प्राप्त किया जा सकता है। यदि P रेखाखण्ड AB को K : 1 के अनुपात में विभाजित करें तो बिन्दु P के निर्देशांक \(\left(\frac{K x_2+x_1}{K+1}, \frac{K y_2+y_1}{K+1}\right)\) होंगे।
विशेष स्थिति : यदि बिन्दु P रेखाखण्ड AB का मध्य-बिन्दु हो, अर्थात् P, AB को 1 में विभाजित करता हो, तो P के निर्देशांक \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

त्रिभुज का क्षेत्रफल :
(i) जब किसी त्रिभुज का आधार और इसका शीर्षलम्ब (ऊँचाई) दिया हो, तो इसका क्षेत्रफल निम्न सूत्र द्वारा परिकलित किया जा सकता है :
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × शीर्ष लम्ब (ऊंचाई)

(ii) यदि किसी त्रिभुज के तीनों शीर्षो के निर्देशांक दिए हाँ तो :
माना कि ABC एक त्रिभुज है, जिसके शीर्ष A(x₁, y₁), B (x₂, y₂) और C (x₃, y₃) हैं बिन्दुओं A, B और C से X-अक्ष पर लम्ब AP, BQ और CR खींचे। बिन्दुओं A, B और C से स्पष्टत: ABQP, APRC और BQRC सभी समलम्ब हैं जैसा कि आकृति में है।

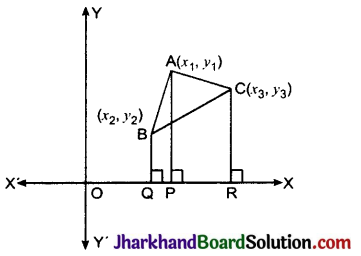
अब, आकृति से स्पष्ट कि
ΔABC का क्षेत्रफल = समलम्ब ABQP का क्षेत्रफल + समलम्ब APRC का क्षेत्रफल – समलम्ब BQRC का क्षेत्रफल
हम यह भी जानते हैं कि

एक समलम्ब का क्षेत्रफल = \(\frac{1}{2}\) (समान्तर भुजाओं का योग) × (उनके बीच की दूरी)
अतः ΔABC का क्षेत्रफल
= \(\frac{1}{2}\)(BQ + AP) QP + \(\frac{1}{2}\)(AP + CR)PR – \(\frac{1}{2}\)(BQ + CR)QR
= \(\frac{1}{2}\)(y₂ + y₁)(x₁ – x₂) + \(\frac{1}{2}\)(y₁ + y₃)(x₃ – x₁) – \(\frac{1}{2}\)(y₂ + y₃)(x₃ – x₂)
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x3(y₁ – y₂)]
अत: ΔABC का क्षेत्रफल निम्न व्यंजक का संख्यात्मक मान है :
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]