JAC Class 10 Maths Notes Chapter 8 त्रिकोणमिति का परिचय

Students should go through these JAC Class 10 Maths Notes Chapter 8 त्रिकोणमिति का परिचय will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 8 त्रिकोणमिति का परिचय

भूमिका :
त्रिकोणमिति के अंग्रेजी शब्द Trigonometry की व्युत्पत्ति ग्रीक शब्दों ‘tri’ (जिसका अर्थ है, तीन), ‘gon’ (जिसका अर्थ है, भुजा) और ‘metron’ (जिसका अर्थ है, माप) से हुई है। वस्तुत: त्रिकोणमिति में एक त्रिभुज की भुजाओं और कोणों के बीच के सम्बन्धों का अध्ययन करते हैं।

पाइथागोरस प्रमेय (Pythagoras Theorem) : “किसी समकोण त्रिभुज में समकोण बनाने वाली भुजाओं के वर्गों का योग त्रिभुज के कर्ण के वर्ग के बराबर होता है।”
(कर्ण)² = (समकोण बनाने वाली एक भुजा)² + (समकोण बनाने वाली दूसरी भुजा)²
चित्र में ΔABC समकोण त्रिभुज है, जिसमें ∠B = 90°, कर्ण = CA तथा समकोण बनाने वाली भुजाएँ क्रमश: AB और BC हैं।

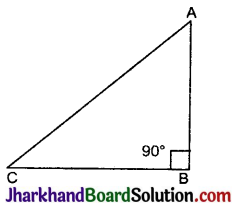
∴ भुजाओं में सम्बन्ध :
(AC)² = (AB)² + (BC)²
यदि दो भुजाओं की माप ज्ञात हो, तो तीसरी भुजा की माप ज्ञात कर सकते हैं।
→ त्रिकोणमिति (Trigonometry): त्रिकोणमिति गणित की वह शाखा है, जिसके अन्तर्गत एक त्रिभुज की भुजाओं और कोणों के बीच के सम्बन्धों का अध्ययन किया जाता है।
→ त्रिकोणमितीय अनुपात (Trigonometric Ratios): एक समकोण त्रिभुज में किसी न्यून कोण के सापेक्ष भुजाओं के अनुपात का अध्ययन त्रिकोणमितीय अनुपात कहलाता है।
→ त्रिकोणमितीय सर्वसमिकाएँ (Trigonometric Identities): एक कोण के त्रिकोणमितीय अनुपातों से सम्बन्धित समीकरण को त्रिकोणमितीय सर्वसमिका कहते हैं। जबकि यह सम्बन्धित कोण (कोणों) के सभी मानों के लिए सत्य होता है।
→ पूरक कोण (Complimentary angles): यदि दो कोणों का योग 90° हो, तो उन कोणों को परस्पर पूरक कोण कहते हैं।
→ sin θ : प्रतीक sin θ का प्रयोग कोण θ, के sinθ के संक्षिप्त रूप में किया गया है।
→ cos θ : प्रतीक cos θ का प्रयोग कोण θ, के cosinθ के संक्षिप्त रूप में किया गया है।
→ tan θ : प्रतीक tan θ का प्रयोग कोण θ के tangent के संक्षिप्त रूप में किया गया है।
→ cot θ : प्रतीक cot θ का प्रयोग कोण θ के, cotangent के संक्षिप्त रूप में किया गया है।
→ sec θ : प्रतीक sec θ का प्रयोग कोण θ के, secant के संक्षिप्त रूप में किया गया है।
→ cosec θ : प्रतीक cosec θ का प्रयोग कोण θ, के cosecant के संक्षिप्त रूप में किया गया है।

त्रिकोणमितीय अनुपात :
समकोण त्रिभुज ABC की भुजाओं के कुछ अनुपातों का उसके न्यूनकोणों के सापेक्ष अध्ययन को त्रिकोणमितीय अनुपात कहते हैं।
समकोण त्रिभुज ABC में ∠B समकोण और न्यूनकोण A के सापेक्ष त्रिकोणमितीय अनुपातों को निम्नांकित प्रकार से परिभाषित कर सकते हैं-


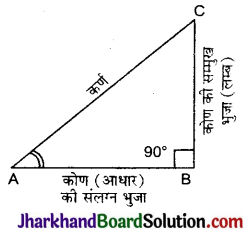
टिप्पणी : cosec A, sec A और cot A अनुपातों sin A, cos A और tan A के क्रमशः व्युत्क्रम हैं।

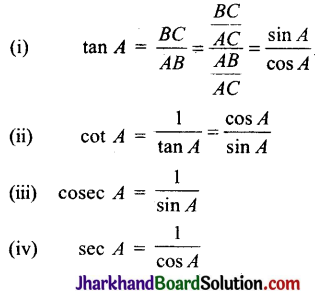
इसलिए, समकोण त्रिभुज के एक न्यूनकोण के त्रिकोणमितीय अनुपात, त्रिभुज के कोण और उसकी भुजाओं की लम्बाई के बीच के सम्बन्ध को व्यक्त करते हैं।

त्रिकोणमितीय अनुपातों में पारस्परिक सम्बन्ध (Relations among Trigonometric Ratios) :
(i) sin और cosec त्रिकोणमितीय अनुपात परस्पर व्युत्क्रम (Reciprocal) हैं।
(ii) cos और sec त्रिकोणमितीय अनुपात परस्पर व्युत्क्रम हैं।
(iii) tan और cot त्रिकोणमितीय अनुपात, परस्पर व्युत्क्रम हैं।

इन्हें निम्न प्रकार से भी व्यक्त किया जा सकता है :

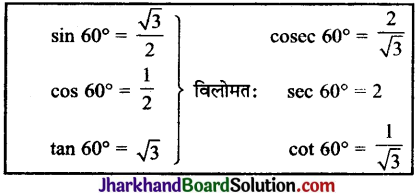
sin² θ + cos² θ =1
sin² θ = 1 – cos² θ
cos² θ = 1 – sin² θ
sec² = 1 + tan² θ
sec² θ – tan² θ = 1
tan² θ = sec²2 θ – 1
cosec² θ = 1 – cot² θ
cosec² θ – 1 = cot² θ
cosec² θ – cot² θ = 1
अग्रांकित सारणी की सहायता से प्रत्येक त्रिकोणमितीय अनुपात को दूसरे त्रिकोणमितीय अनुपातों में परिवर्तित किया जा सकता है :

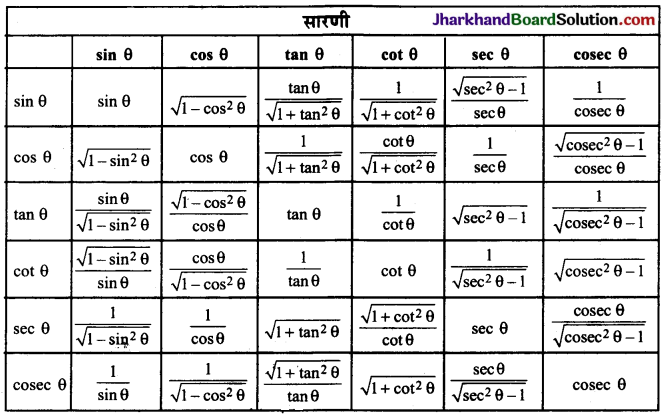
कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात :
0° तथा 90° के त्रिकोणमितीय अनुपात: यदि समकोण ΔABC में कर्ण AC तथा ΔABC’ में कर्ण AC’ बराबर लम्बाई के हैं। दोनों त्रिभुजों से हम देखते हैं कि θ का मान ज्यों-ज्यों बढ़ाते जाते हैं, त्यों-त्यों उसकी सम्मुख भुजा की लम्बाई बढ़ती जाती है। इसके विपरीत θ का मान कम करने पर उसकी सम्मुख भुजा की लम्बाई कम होती जाती है।

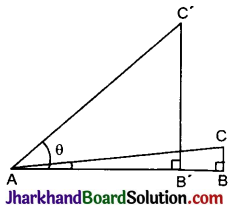
यदि θ का मान घटते घटते शून्य हो जाए, तो उस स्थिति में θ की सम्मुख भुजा BC शून्य और आधार भुजा AB = AC हो जाती है तथा बिन्दु C बिन्दु B के ठीक ऊपर होगा।
∴ sin 0° = \(\frac{B C}{A C}=\frac{0}{A C}\) = 0
तथा cos 0° = \(\frac{A B}{A C}=\frac{A C}{A C}\) = 1 (∵ AB = AC)
tan 0° = \(\frac{\sin 0^{\circ}}{\cos 0^{\circ}}=\frac{0}{1}\) = 0

sin 0° = 0
cos 0° = 1
tan 0° = 0
विलोमतः
cosec 0° = अपरिभाषित
sec 0° = 1
cot 0° = अपरिभाषित
यदि समकोण ΔABC में 6 का मान बढ़ाने पर ∠θ के सामने की भुजा BC की लम्बाई बढ़ती है और आधार भुजा घटती है। θ = 90° की स्थिति में BC भुजा, कर्ण AC के बराबर हो जाती है और बिन्दु के ठीक ऊपर होता है और भुजा AB शून्य हो जाती है।
sin 90° = \(\frac{B C}{A C}=\frac{A C}{A C}=1\)
(∵ 90° पर BC = AC)
तथा cos 90° = \(\frac{A B}{A C}=\frac{0}{A C}\)
tan 90° = \(\frac{\sin 90^{\circ}}{\cos 90^{\circ}}=\frac{1}{0}\) = ∞ (अपरिभाषित)
sin 90° = 1
cos 90° = 0
tan 90° = अपरिभाषित
cosec 90° = 1
विलोमत: sec 90° = अपरिभाषित
cot 90° = 0
30° और 60° के त्रिकोणमितीय अनुपात : एक समबाहु त्रिभुज ABC लेते हैं। जिसका प्रत्येक कोण 60° का होता है।
∴ ∠A = ∠B = ∠C = 60°
शीर्ष A से भुजा BC पर लम्ब AD डालते हैं।

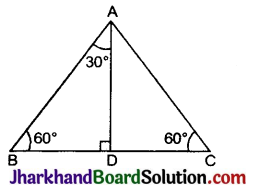
अर्थात् AD ⊥ BC
ΔABD ≅ ΔACD, (RHS सर्वांगसमता नियम से)
∴ BD = DC
∠BAD = ∠CAD (CPCT)
अत: ΔABD एक समकोण Δ है, जिसका कोण D समकोण है।
जहाँ ∠BAD = 30° और ∠ABD = 60°
माना AB = BC = CA = 2a
तब BD = \(\frac{1}{2}\)BC = \(\frac{1}{2}\) × 2a = a
समकोण ΔABD में,
AD² = AB² – BD²
= (2a)² – (a)²
= 4a² – a² = 3a²
AD = a\(\sqrt{3}\)
अब sin 30° = \(\frac{B D}{A B}=\frac{a}{2 a}=\frac{1}{2}\)
cosec 30° = \(\frac{1}{\sin 30^{\circ}}=\frac{1}{\frac{1}{2}}=2\)

45° के त्रिकोणमितीय अनुपात : समकोण ΔABC में, जिसका ∠B = 90° है। यदि एक ∠A = 45°, तो दूसरा ∠B = 45° का होगा।

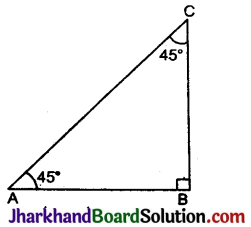
अर्थात्
∠A = ∠C = 45°
∴ AB = BC
माना AB = BC = a
पाइथागोरस प्रमेय से,
AC² = AB² + BC² = a² + a²
⇒ AC² = 2a²
∴ AC = \(\sqrt{2}\)a.

विशेष कोणों के त्रिकोणमितीय अनुपातों की सारणी (Tables of Trigonometric Ratios of Particular Angles)

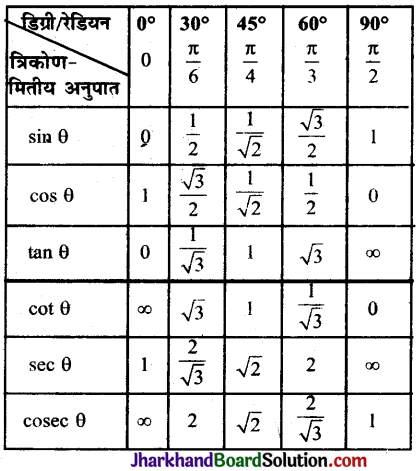
पूरक कोणों के त्रिकोणमितीय अनुपात (Trignometrical Ratios of Complementary Angles) :
यदि दो कोणों का योग 90° के बराबर हो, तो वे दोनों कोण एक-दूसरे के पूरक कहलाते हैं। एक समकोण ΔABC में ∠B समकोण है। इसलिए
∠A + ∠C = 90° ⇒ ∠C = 90° – A
अर्थात् ∠A व ∠C एक-दूसरे के पूरक हैं।

∠A के लिए त्रिकोणमितीय अनुपात :
कर्ण = AC, लम्ब = BC, आधार = AB

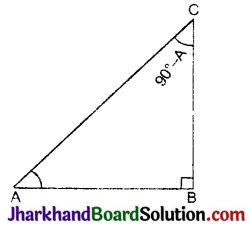
अब ∠C = (90° – A) के लिए त्रिकोणमितीय अनुपात :
कर्ण = AC, आधार = BC, लम्ब = AB
sin ( 90° – A) = लम्ब / कर्ण = \(\frac{A B}{A C}\)
cos (90° – A) = \(\frac{B C}{A C}\)
tan (90° – A) = \(\frac{A B}{B C}\)
cot (90° – A ) = \(\frac{B C}{A B}\)
sec (90° – A) = \(\frac{A C}{B C}\)
cosec (90° – A) = \(\frac{A C}{A B}\)
∠A और ∠C के त्रिकोणमितीय अनुपातों की तुलना करने पर,
sin ( 90° – A) = \(\frac{A B}{A C}\) = cos A
cos (90° – A) = \(\frac{B C}{A C}\) = sin A
tan (90° – A) = \(\frac{A B}{B C}\) = cot A
cot (90° – A ) = \(\frac{B C}{A B}\) = tan A
sec (90° – A) = \(\frac{A C}{B C}\) = cosec A
cosec (90° – A) = \(\frac{A C}{A B}\) = sec A

टिप्पणी : जब हम कोण को बदलेंगे, तो sin θ, cos θ, tan θ, cot θ, sec θ, cosec θ भी परिवर्तित हो जायेंगे। याद रखने के लिए ‘co’ को जोड़िए यदि यह नहीं है तो ‘co’ को हटाइए।

त्रिकोणमितीय सर्वसमिकाएँ :
एक समकोण ΔABC में ∠B समकोण है। पाइथागोरस प्रमेय से,
AB² + BC² = AC² …..(1)

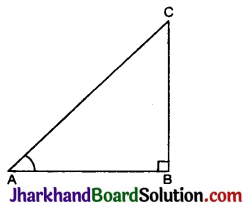
समीकरण (1) के प्रत्येक पदों को AC² से विभाजित करने पर,
\(\frac{A B^2}{A C^2}+\frac{B C^2}{A C^2}=\frac{A C^2}{A C^2}\)
या \(\left(\frac{A B}{A C}\right)^2+\left(\frac{B C}{A C}\right)^2=1\)
या (cos A)² + (sin A)² = 1
अर्थात् cos² A + sin² A = 1, जहाँ 0° ≤ A ≤ 90°
sin² A + cos² A = 1 …..(2)
अब समीकरण (1) को AB² से विभाजित करने पर,
\(\frac{A B^2}{A B^2}+\frac{B C^2}{A B^2}=\frac{A C^2}{A B^2}\)
या \(\left(\frac{A B}{A B}\right)^2+\left(\frac{B C}{A B}\right)^2=\left(\frac{A C}{A B}\right)^2\)
अर्थात् 1 + tan² A = sec² A …..(3)
अब समीकरण (1) को BC2 से विभाजित करने पर,
\(\frac{A B^2}{B C^2}+\frac{B C^2}{B C^2}=\frac{A C^2}{B C^2}\)
⇒ \(\left(\frac{A B}{B C}\right)^2+\left(\frac{B C}{B C}\right)^2=\left(\frac{A C}{B C}\right)^2\)
⇒ cot² A + 1 = cosece² A ….( 4 )
इन सर्वसमिकाओं का प्रयोग करके हम प्रत्येक त्रिकोणमितीय अनुपात को, दूसरे त्रिकोणमितीय अनुपातों के पदों में व्यक्त कर सकते हैं,
sin² θ + cos² θ = 1
⇒ sin² θ = 1 – cos² θ
या cos² θ = 1 – sin² θ
1 + tan² θ = sec² θ
⇒ tan² = sec² θ – 1
या sec² θ – tan² θ = 1
cot² θ + 1 = cosec² θ
⇒ cot² θ = cosec² θ – 1
या cosec² θ – cot² θ = 1