Students should go through these JAC Class 10 Maths Notes Chapter 9 त्रिकोणमिति का अनुप्रयोग will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 10 Maths Notes Chapter 9 त्रिकोणमिति का अनुप्रयोग
भूमिका :
इस अध्याय में हम उन विधियों के विषय में पढ़ेंगे जिनमें त्रिकोणमिति का प्रयोग हमारे आसपास के जीवन से जुड़ा होता है। त्रिकोणमिति की आवश्यकता रवगोलकी में पृथ्वी से ग्रहों और तारों की दूरियाँ परिकलित करने में होती थी। त्रिकोणमिती का प्रयोग भूगोल और नौचालन, मानचित्र बनाने और देशांतर और अक्षांश के सापेक्ष एक द्वीप की स्थिति ज्ञात करने में की जाती है।
इस अध्याय में हम अध्ययन करेंगे कि वास्तविक माप के बिना, त्रिकोणमिति का प्रयोग विभिन्न वस्तुओं की ऊँचाइयाँ और दूरियाँ ज्ञात करने में किया जाता है।
ऊंचाइयाँ और दूरियाँ :
दृष्टि रेखा (Line of sight) : प्रेक्षक की आँख से प्रेक्षक द्वारा देखी गई वस्तु के बिन्दु को मिलाने वाली रेखा को दृष्टि रेखा कहते हैं, अथवा जब हम किसी वस्तु (object) को देखते हैं, तो हमारी आँख और वस्तु को जोड़ने वाली रेखा को दृष्टि रेखा कहते हैं।
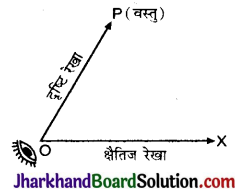
चित्र में आँख बिन्दु पर है और वस्तु की स्थिति P है। अत: OP दृष्टि रेखा होगी।
![]()
पूरक कोण (Complimentary angles) : यदि दो कोणों का योग 90° हो, तो ये कोण पूरक कोण कहलाते हैं।
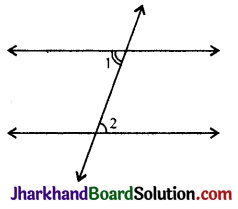
आन्तरिक एकान्तर कोण (Alternate interior angles) : यदि दो रेखाओं को एक तिर्यक रेखा काटती है तो दोनों रेखाओं के अन्दर तिर्यक रेखा के विपरीत दिशा में बने कोण एकान्तर कोण कहलाते हैं, यदि दोनों रेखाएँ परस्पर समान्तर हैं, तो बने आन्तरिक एकान्तर कोण बराबर होते हैं।
उन्नयन कोण (Angle of elevation): जब कोई वस्तु, आँख से ऊपर हो, तो दृष्टि रेखा, क्षैतिज के साथ जो कोण बनता है उसे उन्नयन या उन्नतांश या उन्नति कोण कहते हैं।
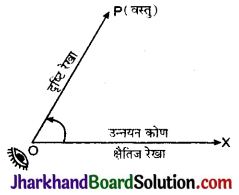
चित्र में आँख बिन्दु पर है और वस्तु (object) की स्थिति P है। अतः OP दृष्टि रेखा है जो क्षैतिज रेखा OX से कोण ∠XOP बनाती है। अतः उन्नयन कोण = ∠XOP
![]()
अवनमन कोण (Angle of depression) : जब कोई वस्तु, आँख से नीचे हो, तो दृष्टि रेखा, क्षैतिज के साथ जो कोण बनता है उसे अवनमन या अवनति कोण कहते हैं।
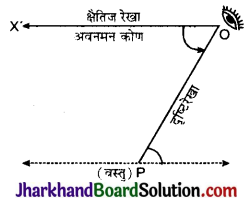
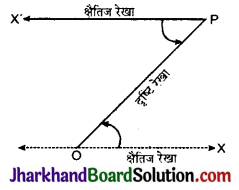
चित्र में आँख बिन्दु पर और वस्तु (object) की स्थिति P है अतः OP दृष्टि रेखा है जो क्षैतिज रेखा OX’ से कोण X’OP बनाती है। अतः अवनमन कोण = X’OP
ऊँचाई एवं दूरी की समस्याओं को हल करते समय निम्नलिखित बिन्दुओं को ध्यान में रखना चाहिए :
(i) सर्वप्रथम प्रश्न को ध्यानपूर्वक पढ़ने के उपरान्त चित्र बनाकर समकोण त्रिभुज का निर्माण करते हैं।
(ii) समकोण त्रिभुज में ज्ञात कोण के त्रिकोणमितीय अनुपातों (sine, cosine, tangent) आदि को ज्ञात भुजा के पदों में व्यक्त करते हैं।
(iii) चित्र में स्पष्ट है कि O का P के सापेक्ष उन्नयन कोण = P का O के सापेक्ष अवनमन कोण।
चित्र में वस्तुओं द्वारा प्रेक्षक की आंख पर अन्तरित अवनमन कोणों के उदाहरण :
