JAC Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.1

Jharkhand Board JAC Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Exercise 1.1

प्रश्न 1.
निम्नलिखित संख्याओं का H. C. F. ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए:
(i) 135 और 225
(ii) 196 और 38220
(iii) 867 और 255
हल:
(i) चरण 1. क्योंकि, संख्याएँ 135 और 225 इस प्रकार हैं कि
225 > 135

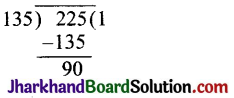
अत: 225 और 135 के लिए यूक्लिड
विभाजन प्रमेयिका का प्रयोग करने पर
225 = 135 × 1 + 90
चरण 2. ∵ शेषफल शून्य नहीं है।
∴ 135 और 90 पर यूक्लिड विभाजन प्रमेयिका प्रयोग करने पर,

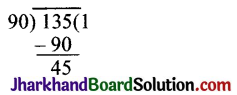
135 = 90 × 1 + 45

चरण 3. 90 और 45 पर यूक्लिड विभाजन प्रमेयिका का प्रयोग करने पर,

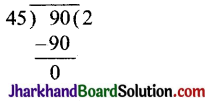
90 = 45 × 2 + 0
∵ शेषफल 0 प्राप्त हो गया।
∴ चरण 3 में भाजक 45 है।
अतः 135 और 225 का H.C.F. = 45

(ii) चरण 1. क्योंकि संख्याएँ 196 और 38220 इस प्रकार हैं कि
38220 > 196

अत: 38220 और 196 के लिए यूक्लिड विभाजन प्रमेयिका का प्रयोग करने पर
38220 = 196 × 195 + 0
∵ शेषफल शून्य प्राप्त हो गया है। इस स्थिति में भाजक 196 है।
∴ 38220 और 196 का H.C.F. = 196

(iii) चरण 1. ∵ संख्याएँ 867 और 255 इस प्रकार हैं कि
867 > 255
अत: 867 और 255 के लिए यूक्लिड विभाजन प्रमेयिका का प्रयोग करने पर

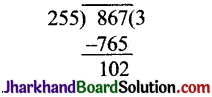
867 = 255 × 3 + 102

चरण 2. ∵ शेषफल 0 नहीं है।
∴ 102 और 255 पर पुन: यूक्लिड विभाजन प्रमेयिका का प्रयोग करने पर,

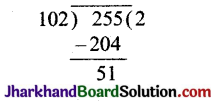
255 = 102 × 2 + 51

चरण 3. 51 और 102 पर पुनः यूक्लिड विभाजन प्रमेयिका का प्रयोग करने पर,

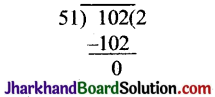
102 = 51 × 2 +0
∵ शेषफल 0 प्राप्त हो गया है।
∴ चरण 3 का भाजक 51 है।
अत: 867 और 255 का H.C.F = 51.

प्रश्न 2.
दर्शाइए कि कोई भी धनात्मक विषम पूर्णांक 6q + 1 या 6q + 3 या 6q + 5 के रूप का होता है, जहाँ 9 कोई पूणांक है।
हल:
माना कि a एक धनात्मक विषम पूर्णांक है। और (b = 6) के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग करने पर,
a = 6q + r, जहाँ 0 ≤ r < 6
∵ 0 ≤ r < 6 के लिए सम्भावित शेषफल 0, 1, 2, 3, 4 और 5 हैं।
∴ a = 6q + 0 या a = 6q + 1
या a = 6q + 2 या a = 6q + 3
या a = 6q + 4 या a= 6q + 5
के रूप का हो सकता है।
जहाँ q = भागफल है तथा a = विषम पूर्णांक हैं।
∴ यह 6q, 6q + 2, 6q + 4 के रूप का नहीं हो सकता है। [सभी 2 से विभाज्य हैं।]
अतः कोई भी धनात्मक विषम पूर्णांक 6q + 1 या 6q + 3 या 6q + 5 के रूप का हो सकता है।

प्रश्न 3.
किसी परेड में 616 सदस्यों वाली एक सेना (आर्मी) की टुकड़ी को 32 सदस्यों वाले एक आर्मी बैंड के पीछे मार्च करना है। दोनों समूहों को समान संख्या वाले स्तम्भों में मार्च करना है। उन स्तम्भों की अधिकतम संख्या क्या है, जिसमें वे मार्च कर सकते हैं ?
हल:
सेना के दो समूहों वाले बैण्ड की कुल संख्या 616 और 32 है।
∵ हमें स्तम्भों की अधिकतम संख्या ज्ञात करनी है।
∴ अधिकतम संख्या के लिए HCF निकालेंगे।
चरण 1. ∵ 616 > 32, ∴ 616 और 32 पर यूक्लिड विभाजन प्रमेयिका का प्रयोग करने पर,

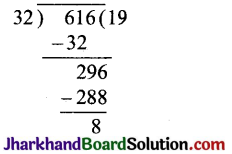
616 = 32 × 19 + 8

चरण 2. ∵ शेषफल 0 नहीं है।
∴ 8 और 32 पर पुन: यूक्लिड विभाजन प्रमेयिका का प्रयोग करने पर,

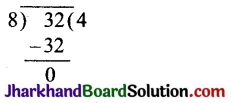
32 = 8 × 4 + 0
यहाँ शेषफल 0 है।
∵ चरण 2 में भाजक 8 है।
∴ 616 और 32 का H.C.F. = 8
अतः मार्च करने के लिए अधिकतम स्तम्भों की संख्या = 8.

प्रश्न 4.
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का वर्ग, किसी पूर्णांक m के लिए 3m या 3m + 1 के रूप का होता है।
हल:
माना a कोई धनात्मक पूर्णांक है तब यह 3q या 3q + 1 या 3q + 2 के रूप का होता है।
अतः इसकी तीन स्थितियाँ सम्भव हैं।
स्थिति I: जब a = 3q
⇒ (a)² = (3q)² = 9q² = 3(3q²) = 3m (जहाँ 3q² = m है)
स्थिति II : a = 3q + 1
⇒ (a)² = (3q + 1)² = 9q² + 6q + 1
= 3q (3q + 2) + 1 = 3m + 1 [जहाँ m = q(3q + 2) है]
स्थिति III: 3q + 2
⇒ (a)² = 3q + 2
(a)² = (3q + 2)²
= 9q² + 12q + 4
= (9q² + 12q + 3) + 1
= 3 (q² + 4q + 1) + 1
= 3m + 1
[जहाँ m = q² + 4q + 1 है]
a² के सभी विस्तारों से स्पष्ट है कि a², 3 से विभाजित होता है और शेषफल या तो शून्य बचता है या 1 बचता है।
अतः किसी धन पूर्णांक का वर्ग किसी पूर्णांक m के लिए 3m या 3m + 1 के रूप का होता है।

प्रश्न 5.
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का घन 9m, 9m + 1 या 9m + 8 के रूप का होता है।
हल:
माना a कोई धनात्मक पूर्णांक है। तब यह 3b या 3b + 1 या 3b + 2 के रूप का होता है।
अतः इसकी तीन स्थितियाँ सम्भव हैं।
स्थिति I: जब a = 3b तो
(a)³ = (3b)³ = 27b³ = 9(3b³) = 9m ……(1)
[जहाँ m = 3b³ है।]
स्थिति II: जब a = 3b + 1 तो
a³ = (3b + 1)³
⇒ a³ = (3b)³ + 3.3b.1 (3b + 1) + (1)³
⇒ a³ = (27b³ + 27b² + 9b) + 1
⇒ a³ = 9[3b³ + 3b² + b] + 1.
a³ = 9m + 1 ……(2)
[जहाँ m = 3b³ + 3b² + b]
स्थिति III: जब a = 3b + 2 तो a³ = (3b + 2)³
⇒ a³ (3b)³ + 3.3b.2(3b+2) + (2)³
⇒ a³ = [27b³ + 18b(3b + 2)] + 8
⇒ a³ = 9[3b³ + 6b² + 4b] + 8
⇒ a³ = 9m + 8
[जहाँ m= 3b³ + 6b² + 4b] … (3)
समीकरण (1), (2) व (3) को देखने पर हम पाते हैं कि a³, 9 से भाग्य है।
तब इन्हें क्रमश: a³ = 9m
या a³ = 9m + 1
या a³ = 9m + 8 लिखा जा सकता है।
अतः किसी धन पूर्णांक का घन 9m, 9m + 1 या 9m + 8 के रूप का होता है।