JAC Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.2

Jharkhand Board JAC Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Exercise 1.2

प्रश्न 1.
निम्नलिखित संख्याओं को अभाज्य गुणनखण्डों के गुणनफल के रूप में व्यक्त कीजिए :
(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429
हल:
(i) दी गई पूर्णांक संख्या 140 है।

140 = 2 × 2 × 5 × 7
= 2² × 5 × 7

(ii) दी गई संख्या 156 है।

156 = 2 × 2 × 3 × 13
= 2² × 3 × 13

(iii) दी गई संख्या 3825 है।

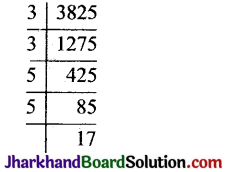
∴ 3825 = 3 × 3 × 5 × 5 × 17
= 3² × 5² × 17

(iv) दी गई संख्या 5005 हैं।

∴ 5005 = 5 × 7 × 11 × 13.

(v) दी गई संख्या 7429 है।

∴ 7429 = 17 × 19 × 23

प्रश्न 2.
पूर्णांकों के निम्नलिखित युग्मों के महत्तम समापवर्तक (H.C.F) और लघुत्तम समापवर्त्य (L.C.M.) ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = H.C.F × L.C.M. है।
(i) 26 और 91
(ii) 510 और 92
(iii) 336 और 54
हल:
(i) दी गई संख्याएँ 26 और 91 हैं।

26 और 91 के उभयनिष्ठ अभाज्य गुणनखण्डों का (न्यूनतम घातों में) गुणनफल = (13)¹ = 13
और 26 और 91 के अधिकतम घातांक में सभी अभाज्य गुणनखण्डों का गुणनफल = 2 × 7 × 13 = 182
अत: महत्तम समापवर्तक (H.C.F.) = 13
तथा लघुत्तम समापवर्त्य (L.C.M.) = 182
अब संख्याओं का गुणनफल = 26 × 91 = 2366
और H.C.F. × L.C.M = 13 × 182 = 2366
अतः संख्याओं का गुणनफल H.C.F. × L.C.M

(ii) दी गई संख्याएँ 510, 92 हैं।
\(\begin{array}{l|l}
2 & 92 \\
\hline 2 & 46 \\
\hline & 23
\end{array}\)
∴ 92 = 2 × 2 × 23 = (2)² × (23)¹
\(\begin{array}{l|r}
2 & 510 \\
\hline 3 & 255 \\
\hline 5 & 85 \\
\hline & 17
\end{array}\)
510 = 2 × 3 × 5 × 17
= (2)¹ × (3)¹ × (5)¹ × (17)¹
92 और 510 के उभयनिष्ठ अभाज्य गुणनखण्डों का (न्यूनतम घाड़ों में) गुणनफल = (2)¹ = 2
अतः H.C.F. = 2
तथा 92 और 510 के अधिकतम घातांक में सभी अभाज्य गुणनखण्डों का गुणनफल
= (2)² × (3)¹ × (5)¹ × (17)¹ × (23)¹
= 23460
अत: L.C.M. = 23460
अतः महत्तम समापवर्तक (H.C.F) = 2 तथा लघुत्तम समापवर्त्य (L..C.M.) = 23460
अब संख्याओं का गुणनफल 92 × 510 = 46920
और H.C.F. × L.C.M. = 2 × 23460
= 46920
अतः संख्याओं का गुणनफलं = H.C.F. × L.C.M.

(iii) दी गई संख्याएँ 336 और 54 हैं।
\(\begin{array}{c|c}
2 & 336 \\
\hline 2 & 168 \\
\hline 2 & 84 \\
\hline 2 & 42 \\
\hline 3 & 21 \\
\hline & 7
\end{array}\)
336 = 2 × 2 × 2 × 2 × 3 × 7= 2⁴ × 3¹ × 7¹
\(\begin{array}{c|r}
2 & 54 \\
\hline 3 & 27 \\
\hline 3 & 9 \\
\hline & 3
\end{array}\)
54 = 2 × 3 × 3 × 3 = 2¹ × 3³
अब दोनों संख्याओं के उभयनिष्ठ अभाग्य गुणनखण्डों का (न्यूनतम घातों में) गुणनफल 2¹ × 3¹ = 6
∴ H.C.F. = 6
और दोनों संख्याओं के अधिकतम घातों में सभी अभाज्य गुणनखण्डों का गुणनफल = 2⁴ × 3³ × 7
= 16 × 27 × 7
= 3024
∴ L.C.M. = 3024
अतः महत्तम समापवर्तक (H.C.F.) = 6
और लघुत्तम समापवर्त्य (L.C.M.) = 3024
∵ संख्याओं का गुणनफल 54 × 336 = 18144
और H.C.F. × L.C.M. = 6 × 3024 = 18144
अतः संख्याओं का गुणनफल = H.C.F. × L.C.M.

प्रश्न 3.
अभाज्य गुणनखण्ड विधि द्वारा निम्नलिखित पूर्णांकों के म. स. (H.C.F.) और ल. स. (L..C.M.) ज्ञात कीजिए :
(i) 12, 15 और 21
(ii) 17, 23 और 29
(iii) 8, 9 और 25
हल:
(i) दी गई संख्याएँ 12, 15 और 21 हैं।
इनके अभाज्य गुणनखण्ड करने पर
12 = 2 × 2 × 3 = (2)² × 3
15 = 3 × 5
तथा 21 = 3 × 7
तीनों संख्याओं के उभयनिष्ठ अभाज्य गुणनखण्डों का (न्यूनतम घातों में) गुणनफल 3¹ = 3
∴ H.C.F. = 3
तथा तीनों संख्याओं के अभाज्य गुणनखण्डों का (अधिकतम घातों में) गुणनफल = 2² × 3 × 5 × 7
= 4 × 3 × 5 × 7 = 420
∴ L.C.M. = 420
अत: महत्तम समापवर्त (H.C.F) = 3
और लघुत्तम समापवर्त्य (L..C.M.) = 420

(ii) दी गई संख्याएँ 17, 23 और 29 हैं।
इनके अभाज्य गुणनखण्ड करने पर,
17 = 1 × 17, 23 = 1 × 23
तथा 29 = 1 × 29
उभयनिष्ठ अभाज्य गुणनखण्डों का (न्यूनतम घार्तो में) गुणनफल = 1
∴ H.C.F. = 1
अभाग्य गुणनखण्डों का (अधिकतम घातों में) गुणनफल = 17 × 23 × 29
= 11339
∴ L.C.M. = 11339
अत: H.CF. = 1 और L.C.M. = 11339

(iii) दी गई संख्याएँ 8, 9 और 25 के अभाज्य गुणनखण्ड करने पर,
8 = 2 × 2 × 2 = 2³
9 = 3 × 3 = 3²
25 = 5 × 5 = 5²
उभयनिष्ठ अभाज्य गुणनखण्डों का (न्यूनतम घातों में) गुणनफल = 1
∴ H.C.F. = 1
अभाज्य गुणनखण्डों का (अधिकतम घातों में) गुणनफल
= (2)³ × (3)² × (5)²
= 8 × 9 × 25 = 1800
∴ L.C.M. = 1800
अतः H.C.F. = 1 और L.C.M. = 1800.

प्रश्न 4.
यदि H.C.F. (306, 657) = 9 तो है। LCM (306, 657) ज्ञात कीजिए।
हल:
हम जानते हैं कि

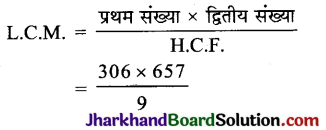
= 34 × 657 = 22338
अत: L.C.M. (306, 657) = 22338

प्रश्न 5.
जाँच कीजिए कि क्या किसी प्राकृत संख्या n के लिए, संख्या 6ⁿ अंक 0 पर समाप्त हो सकती है।
हल:
माना किसी प्राकृत संख्या n के लिए 6ⁿ अंक 0 पर समाप्त होती है।
तब 6ⁿ, 5 से विभाज्य होगा।
∴ 6ⁿ = (2 × 3)ⁿ
अतः स्पष्ट है कि 6ⁿ के अभाज्य गुणनखण्डों में 2 या 3 के अतिरिक्त कोई अन्य अभाज्य गुणनखण्ड नहीं है।
∴ 6ⁿ का कोई गुणनखण्ड 5 नहीं हो सकता है।
अतः 6ⁿ, अंक शून्य पर समाप्त नहीं हो सकती है।

प्रश्न 6.
व्याख्या कीजिए कि 7 × 11 × 13 + 13 और 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 भाज्य संख्याएं क्यों हैं ?
हल:
7 × 11 × 13 + 13 = 13[7 × 11 + 1]
= 13(77 + 1)
= 13 × 78
= 13 × 2 × 3 × 13
= 2 × 3 × 13 × 13
∵ 2, 3 और 13 अभाज्य संख्याएँ हैं। अतः अंकगणित की आधारभूत प्रमेय के अनुसार प्रत्येक भाज्य संख्या अभाज्य संख्याओं के एक गुणनफल के रूप में गुणनखंडित की जा सकती है।
अतः यह एक भाज्य संख्या है।
इसी प्रकार
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
= 5[7 × 6 × 4 × 3 × 2 × 1 + 1]
= 5(1008 + 1)
= 5 × 1009
∵ 5 और 1009 अभाज्य संख्याएँ हैं। अतः अंकगणित की आधारभूत प्रमेय के अनुसार यह एक भाज्य संख्या है।

प्रश्न 7.
किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं। मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारम्भ करके एक ही दिशा में चलते हैं कितने समय बाद वे पुनः प्रारम्भिक स्थान पर मिलेंगे ?
हल:
सोनिया द्वारा मैदान का एक चक्कर लगाने में लगा समय = 18 मिनट
रवि द्वारा मैदान का एक चक्कर लगाने में लगा समय = 12 मिनट
वे पुन: प्रारम्भिक स्थान पर मिलेंगे = L.C.M. (18, 12)
∴ 18 और 12 के अभाज्य गुणनखण्ड हैं:
18 = 2 × 3 × 3
= 2 × (3)²
12 = 2 × 2 × 3
= (2)² × 3
L.C.M. (18, 12) = (2)² × (3)²
= 4 × 9 = 36
अतः सोनिया और रवि प्रारम्भिक स्थान पर 36 मिनट बाद मिलेंगे।