JAC Class 10 Maths Solutions Chapter 11 रचनाएँ Ex 11.1

Jharkhand Board JAC Class 10 Maths Solutions Chapter 11 रचनाएँ Ex 11.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 11 रचनाएँ Exercise 11.1

निम्नलिखित में से प्रत्येक के लिए रचना का औचित्य भी दीजिए :

प्रश्न 1.
7.6 सेमी लम्बा एक रेखाखण्ड खींचिए और इसे 5 : 8 के अनुपात में विभाजित कीजिए। दोनों भागों को मापिए ।
हल :
दिया है : रेखाखण्ड AB = 7.6 सेमी ।
रचना के चरण :
1. एक रेखाखण्ड AB = 7.6 सेमी खींचा।
2. रेखाखण्ड AB के बिन्दु A से न्यूनकोण बनाती हुई किरण AX खींची।
3. किरण AX के परकार की सहायता से (5 + 8) = 13 समान भाग किये।

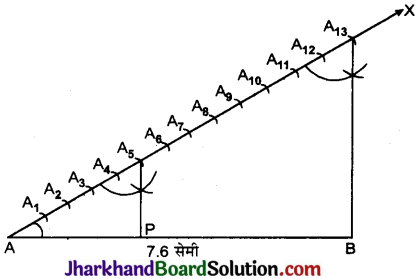
4. BA₁₃ को मिलाया।
5. बिन्दु A₅ से A₁₃B के समान्तर रेखा A₅P खींची जो AB को बिन्दु P पर प्रतिच्छेद करती है अर्थात् ∠BA₁₃A = ∠PA₅A बनाया।
तब AP : PB = 5 : 8
अत: रेखा AB के AP व PB अभीष्ट भाग हैं।
औचित्य (उपपत्ति) : ΔAA₅P तथा AA₁₃B में,
A₁₃B || A₅P
∴ आधारभूत समानुपातिकता प्रमेय से,

अत: बिन्दु P, AB को 5 : 8 के अनुपात में विभाजित करता है।
दोनों भागों को मापने पर,
AP = 2.9 सेमी
तथा PB = 4.7 सेमी।
वैकल्पिक विधि :
रचना 1. एक रेखाखण्ड AB = 7.6 सेमी खींचा।
2. AB के बिन्दु A से AB रेखाखण्ड के ऊपर की ओर न्यूनकोण बनाती हुई किरण AX खींची।
3. AB के बिन्दु B से AB रेखाखण्ड के नीचे की ओर उतना ही कोण (∠BAX) बनाती हुई BY किरण खींची।
4. किरण AX के बिन्दु 4 से समान लम्बाई के आठ बराबर भाग किए अर्थात् AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈ हों।

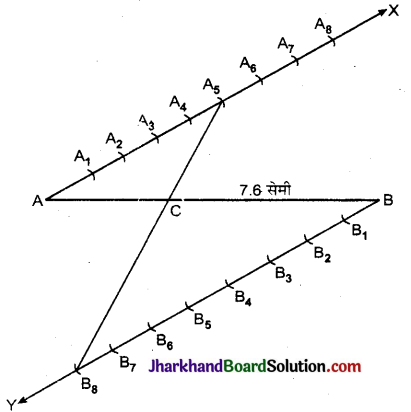
5. किरण BY के बिन्दु B से समान लम्बाई के आठ बराबर भाग किए अर्थात् BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇ = B₇B₈ हो।
6. A₅B₈ को मिलाया, जो AB को बिन्दु C पर काटता है, तब
AC : CB = 5 : 8.
औचित्य (उपपत्ति) : ΔACA₅ और Δ BCB₈ में,
∠ACA₅ = ∠BCB₈ [शीर्षाभिमुख कोण]
∠CAA₅ = ∠CBB₈ [रचना से]
∴ ΔACA₅ ~ ΔBCB₈ [AA समरूपता कसौटी]
∴ समरूप त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

प्रश्न 2.
4 सेमी, 5 सेमी और 6 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{2}{3}\) गुनी हों।
हल :
माना ΔABC है जिसमें AB = 5 सेमी, AC = 4 सेमी और BC = 6 सेमी ।

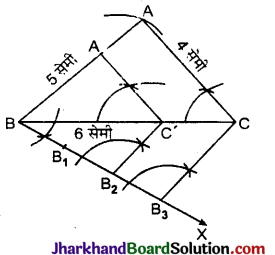
रचना के चरण :

1. एक रेखाखण्ड BC = 6 सेमी खींचा।
2. B को केन्द्र मानकर 5 सेमी की त्रिज्या से एक चाप लगाया।
3. C को केन्द्र मानकर 4 सेमी के बराबर त्रिज्या से चाप लगाइए जो पहले चाप को 4 बिन्दु पर काटता है।
4. AB और AC को मिलाइए। अतः ΔABC वांछित त्रिभुज है।
5. आधार BC के नीचे की ओर कोई न्यूनकोण बनाती BX किरण खींची।
6. BX किरण पर तीन बिन्दु इस प्रकार अंकित किए कि BB₁ = B₁B₂ = B₂B₃ हो ।
7. B₃C को मिलाया।
8. B₃C के समान्तर B₂C’ रेखा खींची जो BC को C’ पर काटती है।
9. बिन्दु C’ से CA के समान्तर C’A’ रेखा खींची अर्थात् ∠ACB = ∠A’C’B बनाया।

इस प्रकार ΔA’BC’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{2}{3}\) गुनी हैं।
औचित्य (उपपत्ति) : अब ΔB₂BC’ और ΔB₃BC में,
∠B = ∠B [उभयनिष्ठ]
∠BB₂C’ = ∠BB₃C [रचना से]
∴ ΔB₂BC’ ~ ΔB₃BC [A-A समरूप कसौटी से]
∴ समरूप त्रिभुजों की संगत भुजाएँ एकसमान अनुपात में होंगी।

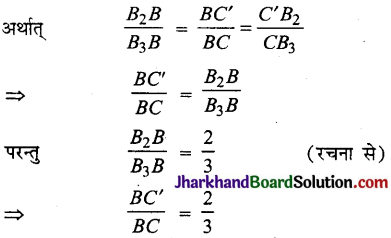
इसी प्रकार ΔA’BC’ और ΔABC में,
∠B = ∠B (उभयनिष्ठ)
∠A’C’B = ∠ACB (रचना से)
∴ ΔA’BC’ ~ ΔABC (A-A समरूपता कसौटी से)
∴ आधारभूत समानुपातिक प्रमेय से,
\(\frac{A’B}{AB}\) = \(\frac{BC’}{BC}\) = \(\frac{C’A’}{CA}\) = \(\frac{2}{3}\)
⇒ A’B = \(\frac{2}{3}\)AB
और BC’ = \(\frac{2}{3}\)BC
C’A’ = \(\frac{2}{3}\)CA.

प्रश्न 3.
5 सेमी, 6 सेमी और 7 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{7}{5}\) गुनी हों।
हल :
माना कि त्रिभुज ABC है जिसमें AB = 7 सेमी, BC = 6 सेमी और AC = 5 सेमी है।

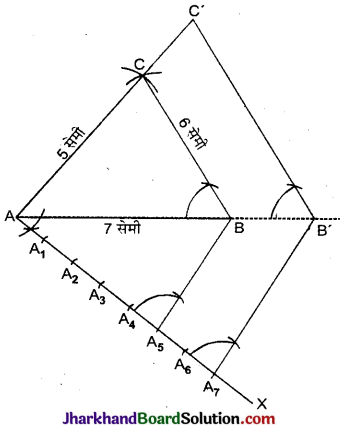
रचना के चरण :

1. सर्वप्रथम AB रेखाखण्ड 7 सेमी खींचा।
2. रेखाखण्ड AB के बिन्दु से परकार में 5 सेमी का चाप लेकर एक चाप लगाया तथा बिन्दु B से 6 सेमी त्रिज्या का दूसरा चाप लगाया जो पहले वाले चाप को C बिन्दु पर काटता है।
3. AC व BC को मिलाया। इस प्रकार ΔABC प्राप्त हुआ।
4. आधार AB के नीचे की ओर कोई न्यूनकोण बनाती हुई AX किरण खींची।
5. किरण AX पर सात बिन्दु A₁, A₂, A₃, A₄, A₅, A₆, A₇ इस प्रकार अंकित किए कि
   AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇
6. BA₅ को मिलाया।
7. बिन्दु A₇ से A₅B के समान्तर एक रेखा A₇B’ खींची। माना कि यह AB को बढ़ाने पर B’ पर इस प्रकार मिलती है कि AB’ = \(\frac{7}{5}\)AB
8. बिन्दु B’ से BC के समान्तर एक रेखा B’C खींची जो AC को बढ़ाने पर C’ पर मिलती है।

ΔAB’C’ अभीष्ट त्रिभुज है।
औचित्य (उपपत्ति) : अब ΔAA₅B और ΔAA₇B’ में,
∠A = ∠A (उभयनिष्ठ)
∠AA₅B = ∠AA₇B’ (संगत कोण)
∴ ΔAA₅B ~ ΔAA₇B’ (A-A समरूपता कसौटी से)
∴ समरूप त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होती हैं।

पुन: ΔABC और ΔAB’C’ में,
∠A = ∠A (उभयनिष्ठ)
∠ABC = ∠AB’C’ (रचना से)
∴ ΔABC ~ ΔAB ‘C’ [A-A समरूपता कसौटी से]
समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं।

अत: ΔAB’C’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{7}{5}\) गुनी हैं।

प्रश्न 4.
आधार 8 सेमी तथा ऊँचाई 4 सेमी के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की 1\(\frac{1}{2}\) गुनी हों।
हल :
माना कि आधार AB = 8 सेमी और ऊँचाई 4 सेमी वाला एक समद्विबाहु ΔABC है।
रचना के चरण :
1. रेखाखण्ड AB = 8 सेमी खींचा।
2. रेखाखण्ड AB का लम्ब समद्विभाजक किया जो AB रेखाखण्ड को M बिन्दु पर काटता है।
3. बिन्दु M को केन्द्र मानकर लम्ब समद्विभाजक में से 4 सेमी काटा, जिस पर C बिन्दु अंकित किया।
4. AC, BC को मिलाकर त्रिभुज ABC प्राप्त किया।
5. बिन्दु A पर AB के नीचे की ओर न्यूनकोण बनाती हुई किरण AX खींची।

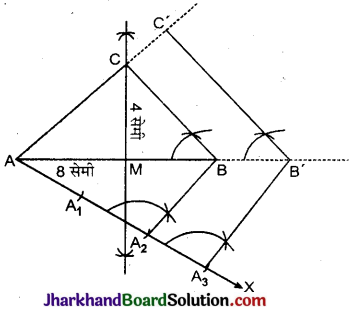
6. AX किरण पर तीन बिन्दु A₁, A₂, A₃ इस प्रकार अंकित किए कि AA₁ = AA₂ = AA₃ हो ।
7. बिन्दु A₂ और B को मिलाया।
8. बिन्दु A₃ से A₂B के समान्तर एक रेखा A₃B’ खींचते हैं जो कि AB को आगे बढ़ाने पर B’ पर काटती है।
9. B’ से BC के समान्तर एक रेखा B’C’ खींचते हैं जो AC को बढ़ ने पर C’ पर मिलती है।
अत: ΔAB’C’ अभीष्ट त्रिभुज है जिसकी भुजाएँ मूल त्रिभुज की 1\(\frac{1}{2}\) गुनी हैं।
औचित्य (उपपत्ति) : ΔA₃AB’ और ΔA₂AB में,
∠A = ∠A (उभयनिष्ठ)
∠B’A₃A = ∠BA₂A (रचना से)
∴ ΔA₃AB’ ~ ΔA₂AB [A-A समरूपता कसौटी से]
∴ समरूप त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होती हैं।

प्रश्न 5.
एक त्रिभुज ABC बनाइए जिसमें BC = 6 सेमी, AB = 5 सेमी और ∠ABC = 60° हो । फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{3}{4}\) गुनी हों।
हल :

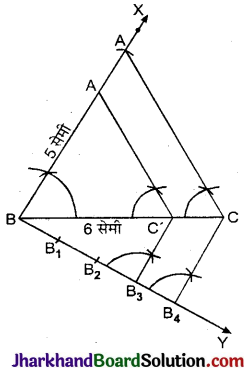
रचना के चरण :

1. रेखाखण्ड BC = 6 सेमी खींचा।
2. रेखाखण्ड BC के बिन्दु B पर 60° का कोण (∠CBX= 60°) बनाया।
3. बिन्दु B को केन्द्र मानकर और 5 सेमी त्रिज्या लेकर एक चाप खींचा जो BX को A पर प्रतिच्छेद करता है।
4. बिन्दु A और C को मिलाया रेखाखण्ड BC के बिन्दु B के नीचे की ओर न्यूनकोण बनाती हुई किरण BY खींची।
5. किरण BY पर चार बिन्दु B₁, B₂, B₃, B₄ इस प्रकार अंकित किए कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ हो। बिन्दु B₄ और C को मिलाया।
6. बिन्दु B₃ से B₄C के समान्तर एक रेखा B₃C’ खींची जो BC को C’ पर प्रतिच्छेद करती है।
7. बिन्दु C’ से CA के समान्तर एक रेखा C’A’ खींची जो BA को A’ पर प्रतिच्छेद करती है।

अतः ΔA’BC’ अभीष्ट त्रिभुज है जिसकी संगत भुजाएँ ΔABC की संगत भुजाओं के \(\frac{3}{4}\) गुनी हैं।
औचित्य (उपपत्ति) :
∵ ΔB₃BC’ और ΔB₄BC में,
∠B = ∠B [उभयनिष्ठ]
∠C’B₃B = ∠CB₄B [ संगत कोण]
ΔB₃BC’ ~ ΔB₄BC [A-A समरूपता कसौटी से]
∴ समरूप त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

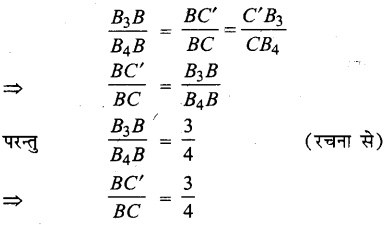
इसी प्रकार ΔBC’A’ और ΔBCA समरूप होते हैं।
∴ उनकी संगत भुजाएँ एक ही अनुपात में होंगी।

अर्थात् ΔA’BC’ की भुजाएँ ΔABC की संगत भुजाओं की \(\frac{3}{4}\) गुनी हैं।

प्रश्न 6.
एक त्रिभुज ABC बनाइए, जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{4}{3}\) गुनी हैं।
हल :
दिया है : ΔABC जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हैं।
रचना के चरण :
1. सर्वप्रथम BC = 7 सेमी का रेखाखण्ड खींचा।
2. BC रेखाखण्ड के बिन्दु B पर 45° का कोण बनाती किरण BD खींची
3. ∵ ∠A + ∠B + ∠C = 180°
105° + 45° + ∠C = 180°
∴ ∠C = 180° – 150° = 30°

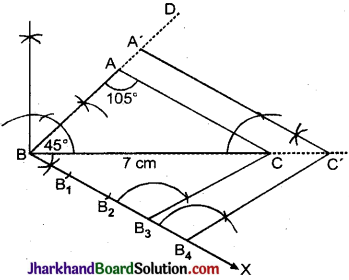
BC रेखाखण्ड के बिन्दु C पर 30° का कोण बनता है। तथा बिन्दु C से एक किरण खींची जो BD को A पर प्रतिच्छेद करती है। इस प्रकार ΔABC प्राप्त हुआ।
4. आधार BC के नीचे बिन्दु B पर कोई न्यूनकोण बनाती हुई किरण BX खींची।
5. BX रेखा पर चार बिन्दु B₁, B₂, B₃, B₄ इस प्रकार अंकित किए कि BB₁ = B₁B₁ = B₂B₃ = B₃B₄ हो ।
6. बिन्दु B₃ को C से मिलाया।
7. बिन्दु B₄ से B₃C के समान्तर एक रेखा B₄C’ खींची जो BC को बढ़ाने पर C’ पर प्रतिच्छेद करती है।
8. बिन्दु C’ से CA के समान्तर एक रेखा C’A’ खींची जो BA को बढ़ाने पर A’ पर प्रतिच्छेद करती है।
अत: ΔA’BC’ अभीष्ट त्रिभुज है जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की \(\frac{4}{3}\) गुनी हैं।
औचित्य (उपपत्ति) : ΔB₄BC’ तथा B₃BC में,
∠B = ∠B (उभयनिष्ठ)
∠C’B₄B = ∠CB₃B (रचना से)
∴ ΔB₄BC’ ~ ΔB₃BC [A-A समरूपता कसौटी से]
∴ समरूप त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होती हैं।

प्रश्न 7.
एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 सेमी तथा 3 सेमी लम्बाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{5}{3}\) गुनी हों।
हल :
दिया है : समकोण त्रिभुज जिसकी समकोण बनाने वाली भुजाएँ 3 सेमी व 4 सेमी हैं।
रचना के चरण :
1. सर्वप्रथम रेखाखण्ड BC = 4 सेमी खींचा।
2. BC के बिन्दु B से BC पर 90° का कोण बनाती हुई BY रेखा खींची और उसमें से BA = 3 सेमी काटी।
3. AC की मिलाया ।
इस प्रकार ΔABC प्राप्त होता है।
4. BC के बिन्दु B पर BC के नीचे की ओर न्यूनकोण बनाती हुई BX किरण खींची।
5. किरण BX पर पाँच बिन्दु B₁, B₂, B₃, B₄, B₅ इस प्रकार अंकित किए कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ हो।

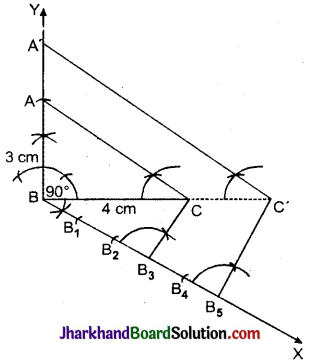
6. बिन्दु B₃ और ‘C’ को मिलाया।
7. B₅ से B₃C के समान्तर एक रेखा B₅C’ खींची जो BC को बढ़ाने पर C’ पर प्रतिच्छेद करे।
8. पुन: C’ से CA के समान्तर एक रेखा C’A’ खींची जो BY पर A’ पर मिलती है। ΔA’BC’ अभीष्ट त्रिभुज है। जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{5}{3}\) गुनी हैं।
औचित्य (उपपत्ति): ΔB₅C’B तथा ΔB₃CB में,
∠B = ∠B (उभयनिष्ठ)
∠C’B₅B = ∠CB₃B ( रचना से)
∴ ΔB₅C’B ~ ΔB₃CB, [A-A समरूपता कसौटी से]
∴ समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं।