Jharkhand Board JAC Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Exercise 12.2
प्रश्न 1.
6 सेमी त्रिज्या वाले एक वृत्त के एक त्रिज्य खण्ड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60° है।
हल :
दिया है : वृत्त की त्रिज्या (r) = 6 सेमी
त्रिज्यखण्ड का कोण (θ) = 60°
त्रिज्यखण्ड का क्षेत्रफल = πr² × \(\frac {θ}{360°}\)
= \(\frac {22}{7}\) × 6 × 6 × \(\frac {60°}{360°}\)
= \(\frac {132}{7}\)
= 18.857 वर्ग सेमी
![]()
प्रश्न 2.
एक वृत्त के चतुर्थांश (quadrant) का क्षेत्रफल ज्ञात कीजिए जिसकी परिधि 22 सेमी है। (π = \(\frac {22}{7}\) लीजिए)
हल :
दिया है : वृत्त की परिधि = 22 सेमी
⇒ 2πr = 22
⇒ r = \(\frac{22}{2 \pi}=\frac{22 \times 7}{2 \times 22}\)
∴ r = \(\frac {7}{2}\)सेमी
वृत्त के चतुर्थांश का क्षेत्रफल = \(\frac {1}{4}\)πr²
= \(\frac{1}{4} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\)
= \(\frac {77}{8}\)
= 9.625 वर्ग सेमी
प्रश्न 3.
एक घड़ी की मिनट की सुई की लम्बाई 14 सेमी है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए ।
हल :
दिया है मिनट की सुई की लम्बाई (r) = 14 सेमी
∵ मिनट की सुई 60 मिनट में 360° का कोण बनाती है।
∴ मिनट की सुई 1 मिनट में \(\frac {360°}{60°}\) = 6° का कोण बनाएगी।
∴ मिनट की सुई 5 मिनट में 6° × 5 = 30° का कोण बनाती है।
r = 14सेमी, θ = 30°
त्रिखण्ड का क्षेत्रफल = πr² × \(\frac {θ}{360°}\)
= \(\frac {22}{7}\) × 14 × 14 × \(\frac {30°}{360°}\)
= \(\frac {154}{3}\) वर्ग सेमी
= 51.33 वर्ग सेमी (लगभग)
द्वितीय विधि :
∵ मिनट की सुई 1 घण्टे या 60 मिनट में लगाती है = 1 चक्कर
∴ मिनट की सुई 1 मिनट में लगाएगी = \(\frac {1}{60}\) चक्कर
∴ मिनट की सुई 5 मिनट में लगाएगी = \(\frac {1}{60}\) × 5 = \(\frac {1}{12}\)चक्कर
मिनट की सुई की लम्बाई (r) = 14 सेमी
तब सुई द्वारा रचित क्षेत्रफल = \(\frac {1}{12}\)πr²
= \(\frac{1}{12}=\frac{22}{7}\) × 14 × 14
= \(\frac {154}{3}\) वर्ग सेमी
= 51.33 वर्ग सेमी (लगभग)
अतः मिनट की सुई द्वारा 5 मिनट में रचित क्षेत्रफल \(\frac {154}{3}\) वर्ग सेमी या 51.33 वर्ग सेमी (लगभग)।
![]()
प्रश्न 4.
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केन्द्र पर एक समकोण अन्तरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
(i) संगत लघु वृत्तखण्ड
(ii) संगत दीर्घ त्रिज्यखण्ड (π = 3.14 का प्रयोग कीजिए) ।
हल :
दिया है : (i) वृत्त की त्रिज्या (r) = 10 सेमी
जीवा द्वारा केन्द्र पर अन्तरित कोण (θ) = 90°
∴ संगत लघु वृत्तखण्ड का क्षेत्रफल

अत: संगत लघु वृत्तखण्ड का क्षेत्रफल = 28.5 वर्ग सेमी।
(ii) संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल

अतः संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल = 235.5 सेमी² ।
प्रश्न 5.
त्रिज्या 21 सेमी वाले वृत्त का एक चाप केन्द्र पर 60° का कोण अन्तरित करता है। ज्ञात कीजिए :
(i) चाप की लम्बाई
(ii) चाप द्वारा बनाए गए त्रिज्यखण्ड का क्षेत्रफल
(iii) संगत जीवा द्वारा बनाए गए वृत्तखण्ड का क्षेत्रफल ।
हल :
दिया है वृत्त की त्रिज्या (r) = 21 सेमी
चाप द्वारा केन्द्र पर बना कोण (θ) = 60°
(i) चाप की लम्बाई (L) = 2πr × \(\frac {θ}{360°}\)
= 2 × \(\frac {22}{7}\) × 21 × \(\frac {60°}{360°}\)
= 22 सेमी
अतः चाप की लम्बाई = 22 सेमी
(ii) चाप द्वारा बनाए गए त्रिज्यखण्ड का क्षेत्रफल
= πr² × \(\frac {θ}{360°}\) = \(\frac {22}{7}\) × (21)² × \(\frac {60°}{360°}\)
= \(\frac {22}{7}\) × 21 × 21 × \(\frac {1}{6}\) = 231 वर्ग सेमी
अतः अभीष्ट त्रिज्यखण्ड का क्षेत्रफल = 231 वर्ग सेमी
(iii) संगत जीवा द्वारा बने वृत्तखण्ड का क्षेत्रफल

अतः वृत्तखण्ड का क्षेत्रफल
= 40.05 वर्ग सेमी।
![]()
प्रश्न 6.
15 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केन्द्र पर 60° का कोण अन्तरित करती है। संगत लघु और दीर्घ वृत्तखण्डों के क्षेत्रफल ज्ञात कीजिए। (π = 3.14 और \(\sqrt{3}\) = 1.73 का प्रयोग कीजिए ।)
हल :
दिया है : वृत्त की त्रिज्या (r) = 15 सेमी
जीवा द्वारा केन्द्र पर अन्तरित कोण (θ) = 60°
∴ संगत लघु वृत्तखण्ड का क्षेत्रफल
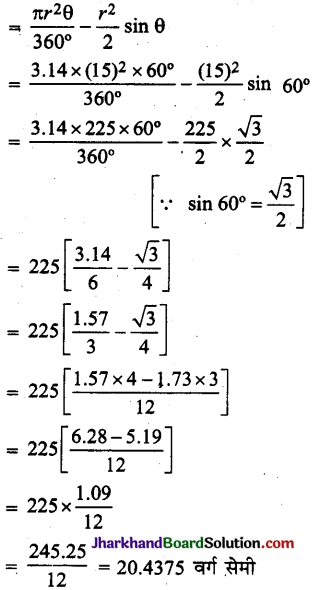
वृत्तखण्ड का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड का क्षेत्रफल
= πr² – 20.4375
= 3.14 × (15)² – 20.4375
= 3.14 × 225 – 20.4375
= 706.50 – 20.4375
= 686.0625 वर्ग सेमी
अतः लघु वृत्तखण्ड का क्षेत्रफल = 20.4375 वर्ग सेमी
तथा दीर्घ वृत्तखण्ड का क्षेत्रफल = 686.0625 वर्ग सेमी
प्रश्न 7.
त्रिज्या 12 सेमी वाले एक वृत्त की कोई जीवा केन्द्र पर 120° का कोण अन्तरित करती है। संगत वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए।
(π = 3.14 और \(\sqrt{3}\) = 1.73 का प्रयोग कीजिए।)
हल :
दिया है : वृत्त की त्रिज्या (r) = 12 सेमी
जीवा द्वारा केन्द्र पर अन्तरित कोण (θ) = 120°
संगत (लघु) वृत्तखण्ड का क्षेत्रफल

अतः अभीष्ट वृत्तखण्ड का क्षेत्रफल
= 88.44 वर्ग सेमी।
![]()
प्रश्न 8.
चित्र में 15 मीटर भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को 5 मीटर लम्बी रस्सी से बाँध दिया गया है। ज्ञात कीजिए-
(i) मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
(ii) चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 मीटर लम्बी रस्सी के स्थान पर 10 मीटर लम्बी रस्सी से बाँध दिया जाए। (π = 3.14 का प्रयोग कीजिए ।)

हल :
वर्गाकार मैदान की भुजा = 15 मीटर
वर्गाकार मैदान का क्षेत्रफल
= (भुजा)² = (15)²
= 225 वर्ग मीटर
(i) ∴ घोड़ा एक 5 मीटर लम्बी रस्सी से बँधा है
∵ वह अधिकतम 5 मीटर त्रिज्या वाले वृत्त के त्रिज्यखण्ड में घास चर सकेगा अर्थात् r = 5 मीटर
तथा मैदान के कोने पर बना कोण (θ) = 90°

अतः घोड़ा को घास चरने योग्य मैदान का क्षेत्रफल = 19.625 वर्ग मीटर
(ii) यदि रस्सी की लम्बाई 10 मीटर कर दी जाए अर्थात् = 10 मीटर

अत: घोड़ा 78.5 वर्ग मीटर क्षेत्र में घास चर सकेगा ।
∴ क्षेत्रफल में वृद्धि = 78.5 – 19.625
= 58.875 वर्ग मीटर ।
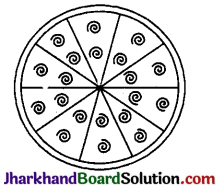
प्रश्न 9.
एक वृत्ताकार बूच (brooch) को चाँदी के तार से बनाया जाना है जिसका व्यास 35 मिमी है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्य-
खण्डों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है तो ज्ञात कीजिए :
(i) कुल वांछित चाँदी के तार की लम्बाई
(ii) बूच के प्रत्येक त्रिज्यखण्ड का क्षेत्रफल
हल :
वृत्ताकार ब्रूच का व्यास = 35 मिमी
त्रिज्या (r) = \(\frac {35}{2}\) मिमी
(i) ∵ चाँदी के ब्रूच के वृत्तीय भाग की माप (परिधि)
= 2πr = π × व्यास
= \(\frac {22}{7}\) × 35 = 110 मिमी
तथा 5 व्यासों की लम्बाई = 35 × 5 = 175 मिमी
∴ चाँदी के तार की कुल लम्बाई = 110 + 175
= 285 मिमी
(ii) ∵ वृत्ताकार ब्रूच का क्षेत्रफल = πr²
= \(\frac {22}{7}\) × (\(\frac {35}{2}\))²
= \(\frac{22}{7} \times \frac{35}{2} \times \frac{35}{2}\)
= \(\frac {1925}{2}\) वर्ग मिमी
∵ ब्रूच को 10 बराबर त्रिज्यखण्डों में विभाजित किया गया है ।
∴ 1 त्रिज्यखण्ड का क्षेत्रफल
= वृत्ताकार ब्रूच का क्षेत्रफल / 10
= \(\frac{1925}{2 \times 10}\)
= \(\frac {385}{4}\)
= 96.25 वर्ग मिमी
अतः ब्रूच के प्रत्येक त्रिज्यखण्ड का क्षेत्रफल
= 96.25 वर्ग मिमी ।
![]()
प्रश्न 10.
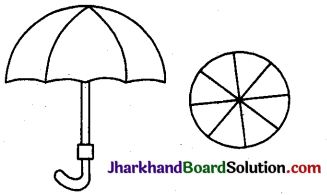
एक छतरी में आठ तानें हैं, जो बराबर दूरी पर लगी हुई हैं। छतरी को 45 सेमी त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।
हल :
दिया है : छतरी की त्रिज्या (r) = 45 सेमी
∵ दो क्रमागत तानों के बीच एक त्रिज्यखण्ड बनता है।
∴ त्रिज्यखण्ड का कोण (θ) = \(\frac {360°}{8}\) = 45°
∴ त्रिज्यखण्ड का क्षेत्रफल = πr² × \(\frac {θ}{360°}\)
= \(\frac {22}{7}\) × (45)² × \(\frac {45°}{360°}\)
= \(\frac {22}{7}\) × 45 × 45 × \(\frac {1}{8}\)
= \(\frac {22275}{28}\)
= 795.536 वर्ग सेमी (लगभग)
अतः दो क्रमागत तानों के बीच का क्षेत्रफल = 795.536 (लगभग) वर्ग सेमी
प्रश्न 11.
किसी कार के दो वाइपर (Wipers) हैं, जो परस्पर कभी आच्छादित नहीं होते हैं। प्रत्येक वाइपर की पत्ती की लम्बाई 25 सेमी है और 115° के कोण तक घूमकर सफाई कर सकता है। पत्तियों की प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ हो जाता है, वह ज्ञात कीजिए।
हल :
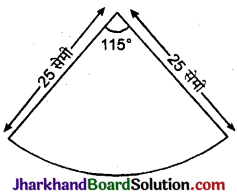
दिया है वाइपर की पत्ती की लम्बाई = त्रिज्या (r) = 25 सेमी
त्रिज्यखण्ड का कोण (θ) = 115°
प्रत्येक वाइपर द्वारा साफ किया गया क्षेत्रफल = त्रिज्यखण्ड का क्षेत्रफल
= πr² × \(\frac {θ}{360°}\)
= \(\frac {22}{7}\) × (25)² × \(\frac {115°}{360°}\)
= \(\frac {22}{7}\) × 625 × \(\frac {115°}{360°}\)
= \(\frac {158125}{252}\) वर्ग सेमी
दोनों वाइपरों के द्वारा साफ किया गया क्षेत्रफल
= 2 × \(\frac{158125}{252}=\frac{158125}{126}\)
= 1254.96 वर्ग सेमी
अतः अभीष्ट सफाई का क्षेत्रफल
= 1254.96 वर्ग सेमी
![]()
प्रश्न 12.
जहाजों को समुद्र में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए एक लाइट हाउस (light house) 80° कोण वाले एक त्रिज्यखण्ड में 16.5 किमी की दूरी तक लाल रंग का प्रकाश फैलाता है। समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाजों को चेतावनी दी जा सके। (π = 3.14 का प्रयोग कीजिए ।)
हल :
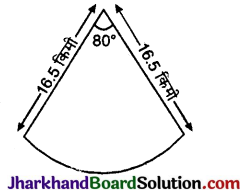
दिया है त्रिज्यखण्ड का कोण (θ) = 80°
त्रिज्यखण्ड की त्रिज्या (r) = 16.5 किमी
= \(\frac {33}{2}\) किमी
समुद्र के उस भाग का क्षेत्रफल जिसमें जहाजों को चेतावनी दी जा सके

अतः अभीष्ट क्षेत्रफल = 189.97 वर्ग किमी
प्रश्न 13.
एक गोल मेजपोश पर छः समान डिजाइन बने हुए हैं जैसा कि आकृति में दर्शाया गया है। यदि मेजपोश की त्रिज्या 28 सेमी है, तो ₹ 0.35 प्रतिवर्ग सेमी की दर से इन डिजाइनों को बनाने की लागत ज्ञात कीजिए। (\(\sqrt{3}\) = 1.7 का प्रयोग कीजिए)
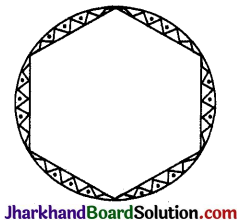
हल :
दिया है : समान डिजाइनों की संख्या = 6
मेजपोश के वृत्त की त्रिज्या (r) = 28 सेमी
प्रत्येक डिजाइन त्रिज्यखण्ड के आकार है और जीवाओं द्वारा केन्द्र पर अन्तरित कोण (θ) = \(\frac {360°}{6}\) = 60°
∴ प्रत्येक वृत्तखण्ड का क्षेत्रफल
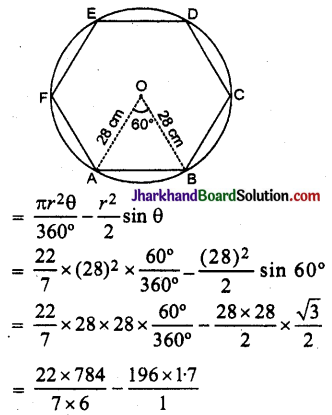
[∵ sin 60° = \(\frac{\sqrt{3}}{2}\)]
= 410.67 – 333.2 = 77.47 वर्ग सेमी
∴ छः वृत्तखण्डों का क्षेत्रफल = 77.47 × 6
= 464.82 वर्ग सेमी
∵ 1 वर्ग सेमी डिजाइन बनाने का खर्च ₹ 0.35
∴ 464.82 वर्ग सेमी डिजाइन बनाने का खर्च
= ₹ 464.82 × 0.35
= ₹ 162.68
अत: डिजाइनों को बनाने की लागत
= ₹ 162.68
![]()
प्रश्न 14.
निम्नलिखित में सही उत्तर चुनिए :
त्रिज्या R वाले वृत्त के उस त्रिज्यखण्ड का क्षेत्रफल जिसका कोण P° है, निम्नलिखित है:
(A) \(\frac {P°}{180°}\) × 2πR
(B) \(\frac {P°}{180°}\) × πR²
(C) \(\frac {P°}{360°}\) × 2πR
(D) \(\frac {P°}{720°}\) × 2πR²
हल :
दिया है त्रिज्यखण्ड का कोण (θ) = P°
वृत्त की त्रिज्या = R

अत: सही विकल्प (D) है।