JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.2

प्रश्न 1.
एक ठोस एक अर्द्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ 1 ऊँचाई उसकी त्रिज्या के बराबर है। इस ठोस का आयतन π के पदों में ज्ञात कीजिए ।
हल :
दिया है,
सेमी हैं तथा शंकु की
अर्द्धगोले की त्रिज्या (r) = शंकु की त्रिज्या (r) = 1 सेमी
तथा शंकु की ऊँचाई (h) = शंकु की त्रिज्या (r)
h = 1 सेमी
अर्द्धगोले का आयतन = \(\frac {2}{3}\)πr³
= \(\frac {2}{3}\) × π × (1)³
= \(\frac {2}{3}\) π घन सेमी
शंक्वाकार भाग का आयतन = \(\frac {1}{3}\)πr²h
= \(\frac {1}{3}\)π × (1)² × (1)
= \(\frac {1}{3}\)π घन सेमी
∴ ठोस का आयतन = अर्द्धगोले का आयतन + शंक्वाकार भाग का आयतन
= (\(\frac {2}{3}\)π + \(\frac {1}{3}\)π) घन सेमी
= π = 3.14 घन सेमी
अतः ठोस का आयतन = 3.14 घन सेमी

प्रश्न 2.
एक इंजीनियरिंग के विद्यार्थी रचेल से एक पतली ऐलुमिनियम की शीट का प्रयोग करते हुए एक मॉडल बनाने को कहा गया जो एक ऐसे बेलन के आकार का हो जिसके दोनों सिरों पर दो शंकु जुड़े हुए हों। इस मॉडल का व्यास 3 सेमी है और इसकी लम्बाई 12 सेमी है। यदि प्रत्येक शंकु की ऊँचाई 2 सेमी हो, तो रचेल द्वारा बनाए गए मॉडल में अन्तर्विष्ट हवा का आयतन ज्ञात कीजिए। (यह मान लीजिए कि मॉडल की आन्तरिक और बाहरी विमाएँ लगभग बराबर हैं।)
हल :
दिया है,
शंकु की त्रिज्या (r) = बेलन की त्रिज्या (r)
= \(\frac {3}{2}\)सेमी = 1.5 सेमी

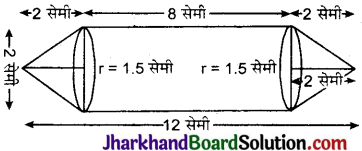
∵ प्रत्येक शंकु की ऊँचाई (h) = 2 सेमी
∴ बेलन की ऊँचाई (H) = (12 – 2 – 2) सेमी
= 8 सेमी
बेलन में हवा का आयतन = बेलन का आयतन + 2 × शंकु का आयतन

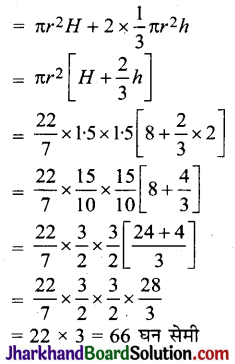
अतः बेलन में हवा का आयतन = 66 घन सेमी

प्रश्न 3.
एक गुलाबजामुन में उसके आयतन की लगभग 30% चीनी की चाशनी होती है। 45 गुलाबजामुनों में लगभग कितनी चाशनी होगी, यदि प्रत्येक गुलाब जामुन एक बेलन के आकार का है, जिसके दोनों सिरे अर्द्ध- गोलाकार हैं तथा इसकी लम्बाई 5 सेमी और व्यास 2.8 सेमी है (देखिए आकृति) ।

हल :
दिया है,
बेलनाकार गुलाब जामुन का व्यास = 2.8 सेमी
गुलाब जामुन के बेलनाकार भाग तथा अर्द्धगोलाकार भाग की उभयनिष्ठ त्रिज्या (r) = \(\frac {2.8}{2}\) = 1.4 सेमी

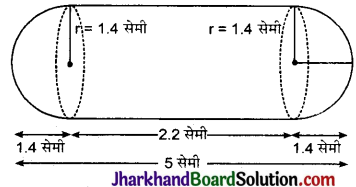
बेलनाकार भाग की ऊँचाई (h) = (5 – 1.4 – 1.4) सेमी
= 2.2 सेमी
एक गुलाबजामुन का आयतन = बेलनाकार भाग का आयतन + 2 × अर्द्धगोलाकार भाग का आयतन
= πr²h + 2 × \(\frac {2}{3}\)πr³ = πr²[h + \(\frac {4}{3}\)r]

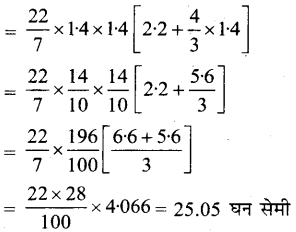
∴ एक गुलाब जामुन का = 25.05 घन सेमी
∴ 45 गुलाब जामुन का आयतन = 45 × 25.05 घन सेमी
= 1127.28 घन सेमी
चीनी की चाशनी का आयतन = 45 गुलाब जामुन के आयतन का 30%
= 1127.28 × \(\frac {30}{100}\)
= 338.184 घन सेमी
अतः चीनी की चाशनी की मात्रा = 338 घन सेमी (लगभग)।

प्रश्न 4.
निम्न चित्र में एक कलमदान घनाभ के आकार की एक लकड़ी से बना है जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढे बने हुए हैं। घनाभ की विमाएँ 15 सेमी × 10 सेमी × 3.5 सेमी हैं। प्रत्येक गड्ढे की त्रिज्या 0.5 सेमी है और गहराई 1.4 सेमी है। पूरे कलमदान में लकड़ी का आयतन ज्ञात कीजिए ।

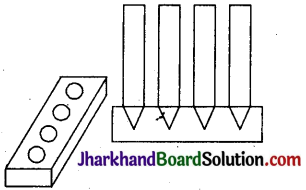
हल :
दिया है,
घनाभ की लम्बाई (l) = 15 सेमी
घनाभ की चौड़ाई (b) = 10 सेमी
घनाभ की ऊँचाई (h) = 3.5 सेमी
शंक्वाकार गड्ढे की त्रिज्या (r) = 0.5 सेमी
शंक्वाकार गड्ढे की गहराई (h’) = 1.4 सेमी
घनाभ का आयतन = l × b × h
= 15 × 10 × 3.5
= 525 घन सेमी
प्रत्येक शंक्वाकार गड्ढे का आयतन = \(\frac {1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × 0.5 × 0.5 × 1.4
= \(\frac {1.1}{3}\) घन सेमी
चार शंक्वाकार गड्ढों का आयतन = 4 × \(\frac {1.1}{3}\) घन सेमी
= \(\frac {4.4}{3}\) = 1.467 घन सेमी
∴ कलमदान में लगी लकड़ी का आयतन
= घनाभ का आयतन – 4 शंक्वाकार गड्ढों का आयतन
= (525 – 1.467) घन सेमी
= 523.533 घन सेमी
अत: पूरे कलमदान में लकड़ी का आयतन
= 523.53 घन सेमी

प्रश्न 5.
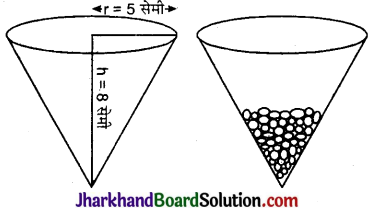
एक बर्तन एक उल्टे शंकु के आकार का है। इसकी ऊँचाई 8 सेमी है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 सेमी है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमें वा प्रत्येक 0.5 सेमी त्रिज्या वाला एक गोला है, डाली जाती हैं 8 तो इसमें से भरे हुए पानी का एक-चौथाई भाग बाहर निकल जाता है। बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए।
हल :
दिया है,
शंकु की त्रिज्या (r) = 5 सेमी
तथा शंकु की ऊँचाई (h) = 8 सेमी
सीसे की गोली की त्रिज्या (r’) = 0.5 सेमी

∴ शंक्वाकार बर्तन या उसमें भरे पानी का आयतन
= \(\frac {1}{3}\)πr²h
= \(\frac {1}{3}\) × π × (5)² × 8
= \(\frac {200π}{3}\) घन सेमी
∵ सीसे की गोलियाँ डालने से भाग \(\frac {1}{4}\) पानी बाहर निकलता है।

प्रश्न 6.
ऊँचाई 220 सेमी और आधार व्यास 24 सेमी वाले एक बेलन, जिस पर ऊँचाई 60 सेमी और त्रिज्या 8 सेमी वाला एक अन्य बेलन आरोपित है, से लोहे का एक स्तम्भ बना है। इस स्तम्भ का द्रव्यमान ज्ञात कीजिए, जबकि दिया है 1 घन सेमी लोहे का द्रव्यमान लगभग 8 ग्राम होता है। (π = 3.14 लीजिए)
हल :
दिया है,
एक बेलन का व्यास = 24 सेमी
बेलन की त्रिज्या (R) = \(\frac {24}{2}\) = 12 सेमी
बेलन की ऊँचाई (H) = 220 सेमी
इस बेलन का आयतन = πr²H
= π × (12)² × 220
= π × 144 × 220 = 31680π घन सेमी

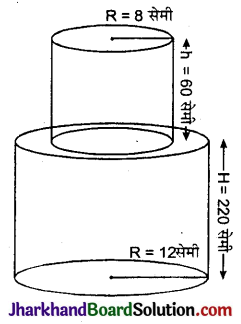
अब, दूसरे बेलन की त्रिज्या (r) = 8 सेमी
तथा ऊँचाई (h) = 60 सेमी
दूसरे बेलन का आयतन
= πr²h
= π × (8)² × 60
= π × 64 × 60
= 3840π घन सेमी
∴ पूरे स्तम्भ का आयतन = एक बेलन का आयतन + दूसरे बेलन का आयतन
= 31680π + 3840π
= 35520π घन सेमी
= 35520 × 3.14 घन सेमी
= 111532.8 घन सेमी
बेलनाकार स्तम्भ का द्रव्यमान
= आयतन × 1 घन सेमी लोहे का भार
= 111532.8 × 8 ग्राम
= 892262.4 ग्राम
= \(\frac {892262.4}{1000}\) किग्रा
= 892.2624 किग्रा = 892.26 किग्रा
अतः स्तम्भ का द्रव्यमान = 892.26 किग्रा

प्रश्न 7.
एक ठोस में, ऊँचाई 120 सेमी और त्रिज्या 60 सेमी वाला एक शंकु सम्मिलित है, जो 60 सेमी त्रिज्या वाले एक अर्द्धगोले पर आरोपित है। इस ठोस को पानी से भरे हुए एक लम्बवृत्तीय बेलन में इस प्रकार सीधा डाल दिया जाता है कि बेलन की तली को स्पर्श करे। यदि बेलन की त्रिज्या 60 सेमी है और ऊंचाई 180 सेमी है तो बेलन में शेष बचे पानी का आयतन ज्ञात कीजिए ।

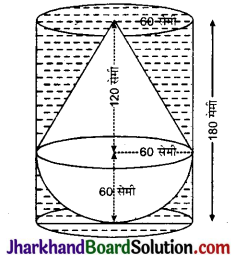
हल :
दिया है,
शंकु की त्रिज्या (r) = अर्द्धगोले की त्रिज्या (r)
= बेलन की त्रिज्या (r)
= 60 सेमी
शंकु की ऊँचाई (h) = 120 सेमी
बेलन की ऊँचाई (H) = 180 सेमी
बेलनाकार बर्तन में पानी का आयतन = πr²H
= \(\frac {22}{7}\) × 60 × 60 × 180
= 2036571.4 घन सेमी
बेलन में डाले गये ठोस का आयतन
= अर्द्धगोले का आयतन + शंकु का आयतन
= \(\frac {2}{3}\)πr³ + \(\frac {1}{3}\)πr²h
= \(\frac {1}{3}\)πr²[2r + h]
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × 60 × 60[2 × 60 + 120]
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × 3600 × 240
= 905142.86 घन सेमी
∴ बेलन में शेष बचे पानी का आयतन = बेलन का आयतन – बर्तन में डाले गए ठोस का आयतन
= 2036571.4 – 905142.86
= 1131428.5 घन सेमी
= \(\frac{1131428.5}{100 \times 100 \times 100}\)घन मीटर
= 1.131 घन मीटर
अतः बेलन में शेष बच्चे पानी का आयतन = 1.131 घन मीटर

प्रश्न 8.
एक गोलाकार काँच के बर्तन की एक बेलन के आकार की गर्दन है जिसकी लम्बाई 8 सेमी है और व्यास 2 सेमी है जबकि गोलाकार भाग का व्यास 8.5 सेमी है। इसमें भरे जा सकने वाले पानी की मात्रा माप कर, एक बच्चे ने यह ज्ञात किया कि इस बर्तन का आयतन 345 सेमी है। जाँच कीजिए कि उस बच्चे का उत्तर सही है या नहीं, यह मानते है हुए कि उपर्युक्त मापन आन्तरिक मापन है और π = 3.14.
हल :

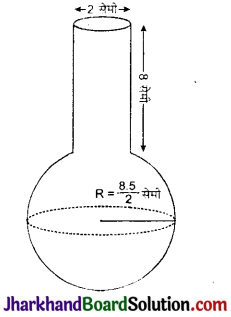
दिया है,
बेलनाकार गर्दन का व्यास = 2 सेमी
बेलनाकार गर्दन की त्रिज्या (r) = \(\frac {2}{2}\) = 1 सेमी
बेलनाकार भाग की ऊँचाई (h) = 8 सेमी
गोलाकार भाग का व्यास = 8.5 सेमी
गोलाकार भाग की त्रिज्या (R) = \(\frac {8.5}{2}\)सेमी
बर्तन में पानी का आयतन = गोलाकार भाग का आयतन + बेलनाकार भाग का आयतन

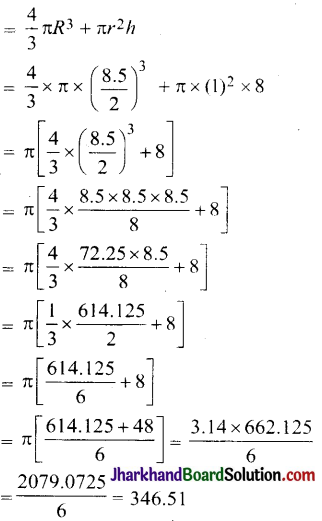
अतः बच्चे का उत्तर 345 घन सेमी गलत है।
बर्तन का आयतन = 346.51 घन सेमी।