JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.5

प्रश्न 1.
व्यास 3 मिमी वाले ताँबे के तार को 12 सेमी लम्बे और 10 सेमी व्यास वाले एक बेलन पर इस प्रकार लपेटा जाता है कि वह बेलन के वक्र पृष्ठ को पूर्णतः ठक लेता है। तार की लम्बाई और द्रव्यमान ज्ञात कीजिए, यह मानते हुए कि ताँबे का घनत्व 8.88 ग्राम प्रति सेमी³ है।
हल :
दिया है:
तार का व्यास (d) = 3 मिमी
तार की त्रिज्या (r) = \(\frac {3}{2}\)मिमी = \(\frac {3}{20}\)सेमी
बेलन की त्रिज्या (R) = \(\frac {10}{2}\) = 5 सेमी
बेलन की ऊँचाई (h) = 12 सेमी

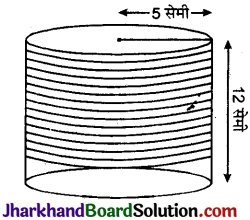
बेलन के आधार का परिमाप = एक लपेटे में प्रयुक्त तार की लम्बाई
= 2πR
= 2 × 3.14 × 5
= 31.4 सेमी

= \(\frac {12}{3}\) × 10 = 40
∴ प्रयुक्त तार की लम्बाई = लपेटों की संख्या × एक लपेटे में प्रयुक्त तार की लम्बाई
प्रयुक्त तार की लम्बाई (H) = 40 × 31.4 सेमी = 1256 सेमी
प्रयुक्त तार का आयतन = πr²H
= \(\frac{22}{7} \times \frac{3}{20} \times \frac{3}{20}\) × 1256
= 88.817 घन सेमी
∵ 1 घन सेमी का द्रव्यमान = 8.88 ग्राम
∴ 88.817 घन सेमी का द्रव्यमान = 8.88 × 88.817
= 788 ग्राम (लगभग) ।
अतः तार की लम्बाई = 1256 सेमी तथा तार का द्रव्यमान = 788 ग्राम (लगभग)

प्रश्न 2.
एक समकोण त्रिभुज, जिसकी भुजाएँ 3 सेमी और 4 सेमी हैं (कर्ण के अतिरिक्त) को उसके कर्ण के परित: घुमाया जाता है। इस प्रकार प्राप्त द्वि-शंकु (double cone) के आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (ग का मान जो भी उपयुक्त लगे, प्रयोग कीजिए ।)
हल :
माना कि ABC एक समकोण त्रिभुज है जिसमें ∠B = 90°, AB = 4 सेमी, BC = 3 सेमी
समकोण ΔABC का क्षेत्रफल
= \(\frac{3 \times 4}{2}\) = 6 वर्ग सेमी

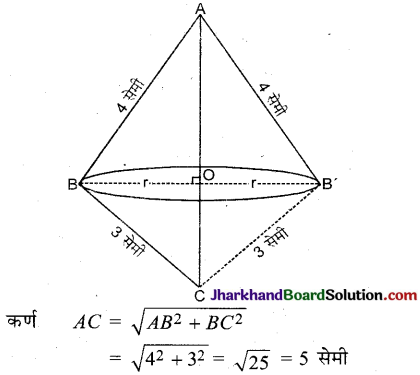
∵ AC पर BOB’ लम्ब है। माना BO = r सेमी है, तो
ΔABC का क्षेत्रफल = \(\frac{A C \times B O}{2}=\frac{5 \times r}{2}\)
6 = \(\frac {5r}{2}\) [∵ दोनों ΔABC के क्षेत्रफल हैं]
∴ r = \(\frac{6 \times 2}{5}\) = 2.4 सेमी
अतः समकोण ΔABC के परिक्रमण से बने द्वि-शंकु की त्रिज्या = 2.4 सेमी
द्वि-शंकु (double cone) का आयतन = शंकु (ABB’) का आयतन + शंकु (CBB’) का आयतन
= \(\frac {1}{3}\)πr²(AO) + \(\frac {1}{3}\)πr² (OC)
= \(\frac {1}{3}\)πr² (AO + OC) = \(\frac {1}{3}\)πr² (AC)
= \(\frac {1}{3}\)π × 2.4 × 2.4 × 5 = 9.6π घन सेमी
= 9.6 × 3.14 घन सेमी = 30.144 घन सेमी
और द्विशंकु का पृष्ठीय क्षेत्रफल = शंकु (ABB’) का वक्र पृष्ठीय क्षेत्रफल + शंकु (CBB’) का वक्र पृष्ठीय क्षेत्रफल
= πr (AB) + πr (BC) = πr (AB + BC)
= 3.14 × 2.4 × (4 + 3)
= 3.14 × 2.4 × 7 = 52.75 वर्ग सेमी
अतः द्विशंकु का आयतन 30.144 घन सेमी
और द्विशंकु का पृष्ठीय क्षेत्रफल = 52.752 वर्ग सेमी

प्रश्न 3.
एक टंकी, जिसके आन्तरिक मापन 150 सेमी × 120 सेमी × 110 सेमी हैं, में 129600 समी³ पानी है। इस पानी में कुछ छिद्र वाली ईंटें तब तक डाली जाती हैं, जब तक कि टंकी पूरी ऊपर तक भर न जाए। प्रत्येक ईंट अपने आयतन का \(\frac {1}{17}\) पानी सोख लेती है। यदि प्रत्येक ईंट की माप 22.5 सेमी × 7.5 सेमी × 6.5 सेमी है, तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं, ताकि उसमें से पानी बाहर न बहे ?
हल :
दिया है,
टंकी में पानी का आयतन = 129600 सेमी³
टंकी का आयतन = 150 × 120 × 110
= 1980000 सेमी³
प्रत्येक ईंट का आयतन = 22.5 × 7.5 × 6.5
= 1096.875 सेमी³
माना टंकी में n ईंटें डालने पर टंकी पानी से ऊपर तक भर जाएगी।
∵ n ईंटों का आयतन = 1096.875n घन सेमी
∴ ईंटों द्वारा शोषित पानी का आयतन
= 1096.875 n × \(\frac {1}{17}\)
= \(\frac {1096.875 n}{17}\)घन सेमी
टंकी में शेष बचे पानी का आयतन
= (129600 – \(\frac {1096.875 n}{17}\)) घन सेमी
टंकी का आयतन = n ईंटों का आयतन + टंकी में पानी का आयतन
⇒ 1980000 = 1096.875 n + 129600 – \(\frac {1096.875 n}{17}\)
⇒ 1980000 – 129600 = 1096.875 n – \(\frac {1096.875 n}{17}\)
⇒ 1850400 = 1096.875 n [1 – \(\frac {1}{17}\)]
⇒ 1850400 = 1096.875 n × \(\frac {16}{17}\)
⇒ 1096.875 n = \(=\frac{1850400 \times 17}{16}\)
⇒ n = \(\frac{1850400 \times 17}{16 \times 1096.875}\)
= 1792.4
≈ 1792 (लगभग)
अतः टंकी में डाली गई ईंटों की संख्या = 1792

प्रश्न 4.
किसी महीने के 15 दिनों में, एक नदी की घाटी में 10 सेमी वर्षा हुई। यदि इस घाटी का क्षेत्रफल 97280 वर्ग किमी है तो दर्शाइए कि कुल वर्षा लगभग तीन नदियों के सामान्य पानी के योग के समतुल्य थी, जबकि प्रत्येक नदी 1072 किमी लम्बी, 75 मीटर चौड़ी और 3 मीटर गहरी है।
हल :
दिया है,
प्रत्येक नदी की लम्बाई = 1072 किमी चौड़ाई = 75 मी तथा गहराई = 3 मी
प्रत्येक नदी का आयतन
= 1072 किमी × 75 मीटर × 3 मीटर = 1072 × 1000 × 75 × 3 घन मीटर
= 241200000 घन मीटर
∴ तीनों नदियों के कुल पानी का आयतन = 3 × 241200000 घन मीटर
= 723600000 घन मीटर
∴ घाटी का क्षेत्रफल = 7280 वर्ग किमी (दिया है)
= 7280 × (1000)² वर्ग मीटर
= 7280000000 वर्ग मीटर
∴ वर्षा के पानी का आयतन
= 7280000000 × \(\frac {10}{100}\) घन मीटर (∵ 10 सेमी = \(\frac {10}{100}\)मीटर)
= 728000000 घन मीटर
∵ वर्षा के पानी का आयतन तीनों नदियों के पानी के आयतन के बराबर नहीं है।
अतः प्रश्न में दिए गए तथ्य असंगत हैं।

प्रश्न 5.
टीन की बनी हुई एक तेल की कुप्पी 10 सेमी लम्बे एक बेलन में एक शंकु के छिन्नक को जोड़ने से बनी है। यदि इसकी कुल ऊंचाई 22 सेमी है, बेलनाकार भाग का व्यास 8 सेमी है और कुप्पी के ऊपरी 1 सिरे का व्यास 18 सेमी है, तो इसके बनाने में लगी टीन की चादर का क्षेत्रफल ज्ञात कीजिए। (देखिए आकृति)

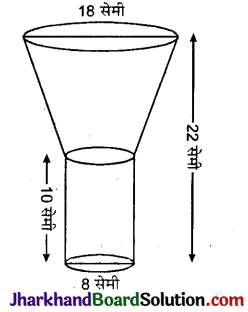
हल :
दिया है,
कुप्पी के ऊपरी सिरे का व्यास = 18 सेमी
∴ कुप्पी के ऊपरी सिरे की त्रिज्या (R) = \(\frac {18}{2}\) = 9 सेमी
कुप्पी के आधार का व्यास = 8 सेमी
∴ कुप्पी के आधार की त्रिज्या (r) = \(\frac {8}{2}\) = 4 सेमी
बेलनाकार भाग की ऊँचाई (h) = 10 सेमी
शंकु के छिन्नक की ऊँचाई (H) = (22 – 10) = 12 सेमी
शंकु के छिन्नक की तिर्यक ऊँचाई (l) = \(\sqrt{H^2+(R-r)^2}\)
= \(\sqrt{(12)^2+(9-4)^2}\)
= \(\sqrt{(12)^2+(5)^2}\)
= \(\sqrt{144+25}\)
= \(\sqrt{169}\)
= 13 सेमी
शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल
= πr (R + r) l
= n (9 + 4) × 13 = 169π वर्ग सेमी
बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल = 2πrh = 2π × 4 × 10 = 80π वर्ग सेमी
टीन की चादर का क्षेत्रफल = बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल + शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल
= 80π + 169π = 249π
= 249 × \(\frac{22}{7}=\frac{5478}{7}\) = 782\(\frac {4}{7}\)सेमी²
= 782.57 वर्ग सेमी
अतः प्रयुक्त की गई चादर का कुल क्षेत्रफल = 782.57 वर्ग सेमी।

प्रश्न 6.
शंकु के छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, वक्र पृष्ठीय क्षेत्रफल और सम्पूर्ण पृष्ठीय क्षेत्रफल के उन सूत्रों को सिद्ध कीजिए, जो अनुच्छेद 13.5 में दिये गए हैं।
हल :

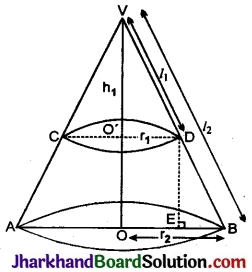
माना एक शंकु (V, AB) का शीर्ष V, आधार की त्रिज्या r₂ और तिर्यक ऊँचाई l₂ है। इस शंकु के शीर्ष V से h₁ नीचे स्थित बिन्दु O’ से आधार के समान्तर एक शंकु (V, CD) काटा गया है जिसकी त्रिज्या r₁ तथा तिर्यक ऊँचाई l₁ है।
बिन्दु D से आधार पर लम्ब DE खींचा।
ΔVO’D तथा ΔDEB में,
∠VO’D = ∠DEB
(VO’ और DE दोनों ही आधार पर लम्बवत् हैं)
∠VDO’ = ∠DBE
(दोनों शंकुओं के आधार परस्पर समान्तर हैं)
∴ ΔVO’D और ΔDEB समरूप हैं,

छिन्नक का वक्र पृष्ठीय क्षेत्रफल = शंकु (V, AB) का वक्र पृष्ठीय क्षेत्रफल – शंकु (V, CD) का वक्र पृष्ठीय क्षेत्रफल
= πr₂l₂ – πr₁l₁ = πr₂(l₁ + BD) – πr₁l₁
= πr₂l₁ + πr₂BD – πr₁l₁
= π(r₂ – r₁) × [r₁ / r₂ – r₁]l + πr₂l
= πr₁l + πr₂l
अतः छिन्नक का वक्र पृष्ठीय क्षेत्रफल
= π(r₁ + r₂)l
और छिन्नक का सम्पूर्ण पृष्ठीय क्षेत्रफल = वक्र पृष्ठीय क्षेत्रफल + पहले सिरे का क्षेत्रफल + दूसरे सिरे का क्षेत्रफल
= π(r₁ + r₂)l + πr₁² + πr₂²
= π(r₁ + r₂)l + π(r₁² + r₂²)

प्रश्न 7.
शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, आयतन का वह सूत्र सिद्ध कीजिए, जो अनुच्छेद 13.5 में दिया गया है।
हल :
मान शंकु (V, AB) का शीर्ष V, आधार की त्रिज्या r₂ है। इस शंकु के शीर्ष V से h₁ नीचे स्थित बिन्दु O’ से आधार के समान्तर एक शंकु (V, CD) काटा गया है जिसकी त्रिज्या r₁ है।

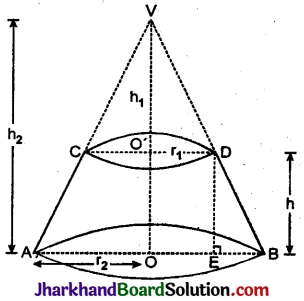
∴ शंकु (V, AB) का आयतन = \(\frac {1}{3}\)πr₂²h₂
और शंकु (V, CD) का आयतन = \(\frac {1}{3}\)πr₁²h₁
∴ छिन्नक का आयतन = शंकु (V, AB) का आयतन – शंकु (V, CD) का आयतन