JAC Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.2

Jharkhand Board JAC Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 2 बहुपद Exercise 2.2

प्रश्न 1.
निम्न द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए:
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x.
(iv) 4u² + 8u
(v) t² – 15
(vi) 3x² – x – 4
हल:
(i) दिया गया बहुपद f(x) = x² – 2x – 8
= x² – (4 – 2) x – 8 = x² – 4x + 2x – 8
= x(x – 4) + 2(x – 4) = (x – 4) (x + 2)
∴ x² – 2x – 8 = (x – 4) (x + 2)
बहुपद f(x) के शून्यक ज्ञात करने के लिए f(x) शून्य होगा।
⇒ f(x) = 0
अतः यदि x – 4 = 0 हो, तो x = 4
या फिर x + 2 = 0 हो, तो x = -2
अत: बहुपद x² – 2x – 8 के शून्यक = 4 और -2
बहुपद के गुणांकों और शून्यकों में सम्बन्ध :
शून्यकों का योग = 4 + (-2) = 2

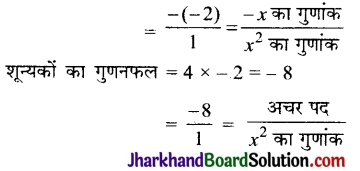
अत: बहुपद के गुणांकों और शून्यकों के बीच सम्बन्ध सत्य है।

(ii) दिया हुआ बहुपद = 4s² – 4s + 1
= (28)² – 2 (2s). 1 + (1)²
= (2s – 1)²
बहुपद f(x) के शून्यक ज्ञात करने के लिए f(x) शून्य होगा।
⇒ (2s – 1)² = 0
यदि (2s – 1)² = 0 ⇒ 2s – 1 = 0 ⇒ s = \(\frac{1}{2}\)
यहाँ बहुपद के शून्यक समान हैं।
अतः बहुपद के शून्यक \(\frac{1}{2}\) और \(\frac{1}{2}\) हैं।

बहुपद के शून्यकों तथा गुणांकों में सम्बन्ध :

अतः बहुपद के शून्यकों और गुणांकों के मध्य सम्बन्ध सही है।

(iii) दिया गया बहुपद f(x)
= 6x² – 3 – 7x = 6x² – 7x – 3
= 6x² – (9 – 2) x – 3
= 6x² – 9x + 2x – 3
= 3x (2x – 3) + 1(2x – 3)
= (2x – 3) (3x + 1)
∴ बहुपद 6x² – 3 – 7x = (2x – 3 ) (3x + 1)
बहुपद 6x² – 7x – 3 के शून्यक ज्ञात करने के लिए f(x) शून्य होगा।
⇒ f(x) = 0
यदि 2x – 3 = 0 हो, तो 2x = 3 ⇒ x = \(\frac{3}{2}\)
और यदि 3x + 1 = 0 हो, तो 3x = -1 ⇒ x = –\(\frac{1}{3}\)
अत: बहुपद के शून्यक \(\frac{3}{2},-\frac{1}{3}\)

बहुपद के शून्यकों तथा गुणांकों में सम्बन्ध :

अतः बहुपद के गुणांकों और के बीच सम्बन्ध सत्य है।

(iv) दिया गया बहुपद f(u) = 4u² + 8u
⇒ f(u) = 4u(u + 2)
बहुपद f(u) के शून्यक ज्ञात करने के लिए f(u) शून्य होगा।
∴ f(u) = 0 ⇒ 4u(u + 2) = 0
u = 0 या u + 2 = 0 ⇒ u = 0 या u = -2
अतः f(u) के शून्यक 0 और -2 है।

बहुपद के शून्यकों तथा गुणांकों में सम्बन्ध :

अतः बहुपद के गुणांकों और शून्यकों के बीच सम्बन्ध सत्य है।

(v) दिया गया बहुपद f(t) = t² – 15 है।
बहुपद f(t) के शून्यक ज्ञात करने के लिए f(x) शून्य होगा।
t² = 15 या t = ±\(\sqrt{15}\)
अत: बहुपद t² – 15 के शून्यक = +\(\sqrt{15}\), –\(\sqrt{15}\)

बहुपद के गुणांकों और शून्यकों के मध्य सम्बन्ध :

अतः बहुपद के गुणांकों और शून्यकों के मध्य सम्बन्ध सत्य है।

(vi) दिया गया बहुपद f(x) = 3x² – x – 4
= 3x² – (4 – 3)x – 4
= 3x² – 4x + 3x – 4
= x(3x – 4) + 1 (3x – 4)
= (3x – 4) (x + 1)
∴ 3x² – x – 4 = (3x – 4) (x + 1)
बहुपद f(x) के शून्यक ज्ञात करने के लिए f(x) शून्य होगा।
⇒ f(x) = 0
(3x – 4 ) (x + 1) = 0
यदि 3x – 4 = 0 हो, तो 3x = 4 ⇒ x = \(\frac{4}{3}\)
या फिर x + 1 = 0 हो, तो x = -1
अत: बहुपद के शून्यक \(\frac{4}{3}\) और -1 हैं।

बहुपद के शून्यकों तथा गुणांकों में सम्बन्ध :

अतः बहुपद के गुणांकों और शून्यकों के बीच सम्बन्ध सत्य है।

प्रश्न 2.
एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों का योग तथा गुणनफल क्रमश: हैं:
(i) \(\frac{1}{4}\) और -1
(ii) \(\sqrt{2}\) और \(\frac{1}{3}\)
(iii) 0 और \(\sqrt{5}\)
(iv) 1 और 1
(v) –\(\frac{1}{4}\) और \(\frac{1}{4}\)
(vi) 4 और 1
हल:
यदि द्विघात बहुपद f(x) के शून्यक ज्ञात हो तो निम्न सूत्र द्वारा अभीष्ट बहुपद ज्ञात करते है
f(x) = k{x² – (शून्यकों का योग) x + शून्यकों का गुणनफल},
जहाँ k = एक वास्तविक संख्या
(i) माना f(x) वह बहुपद है जिसके शून्यकों का योग \(\frac{1}{4}\) और गुणनफल – 1 हैं।

अतः अभीष्ट बहुपद 4x² – x – 4 या K(4x² – x – 4) हैं।

(ii) माना f(x) वह द्विघात बहुपद है, जिसके शून्यकों का योग \(\sqrt{2}\) और गुणनफल \(\frac{1}{3}\) हैं।
f(x) = \(k\left(x^2-\sqrt{2} x+\frac{1}{3}\right)\)
= \(k\left(\frac{3 x^2-3 \sqrt{2} x+1}{3}\right)\)
= \(\frac{k}{3}\left(3 x^2-3 \sqrt{2} x+1\right)\)
= K(3x² – 3\(\sqrt{2}\)x + 1)
जहाँ \(\frac{k}{3}\) एक अचर पद है/ वास्तविक संख्या है।
अत: अभीष्ट बहुपद 3x² – 3\(\sqrt{2}\)x + 1
या K (3x² – 3\(\sqrt{2}\)x + 1 ) है।

(iii) माना f(x) वह द्विघात बहुपद है जिसके शून्यकों का योग 0 और गुणनफल \(\sqrt{5}\) हैं।
∴ f(x) = k[x² – 0, x + \(\sqrt{5}\) = k[x² + \(\sqrt{5}\)]
(जहाँ k अचर पद है)
अतः अभीष्ट बहुपद x² + \(\sqrt{5}\) है।

(iv) माना f(x) वह द्विघात बहुपद है जिसके शून्यकों का योगफल 1 और गुणनफल 1 हैं।
∴ f(x) = k (x² – 1x + 1)
= k(x² – x + 1), जहाँ k अचर पद है।
अतः अभीष्ट बहुपद x² – x + 1 है।

(v) माना f(x) वह द्विघात बहुपद है जिसके शून्यकों का योग –\(\frac{1}{4}\) औरगुणनफल \(\frac{1}{4}\) हैं।

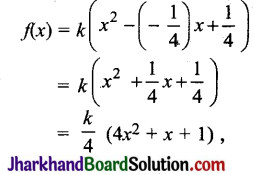
(जहाँ \(\frac{k}{4}\) एक अचर पद है)
अतः अभीष्ट बहुपद 4x² + x + 1 है।

(vi) माना f(x) वह द्विघात बहुपद है जिसके शून्यक का योग 4 और गुणनफल 1 हैं।
∴ f(x) = k[x² – 4x + 1], (जहाँ k अचर पद है)
अत: अभीष्ट बहुपद x² – 4x + 1 है।