JAC Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.4

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Exercise 5.4

प्रश्न 1.
A. P. 121, 117, 113, का कौन-सा पद सबसे पहला ऋणात्मक पद होगा ?
हल:
दी गई A. P. है : 121 117, 113, …
प्रथम पद a = a₁ = 121; a₂ = 117; a₃ = 113
सार्वन्तर d = a₂ – a₁ = 117 – 121 = – 4
सूत्र a_n = a + (n – 1)d का प्रयोग करने पर,
⇒ a_n = 121 + (n – 1 ) (- 4)
= 121 – 4n + 4
= 125 – 4n
प्रश्नानुसार,
a_n < 0
⇒ 125 – 4n < 0
⇒ 4n > 125
⇒ n > \(\frac{125}{4}\)
⇒ n > 31\(\frac{1}{4}\)
⇒ n > 31.25
⇒ n < 32
क्योंकि n एक पूर्णांक है।
अत: 32वाँ पद पहला ऋणात्मक पद होगा।

प्रश्न 2.
किसी AP के तीसरे और सातवें पदों का योग 6 है और उनका गुणनफल 8 है। इस A. P. के प्रथम 16 पदों का योग ज्ञात कीजिए।
हल:
माना दी गई A.P का प्रथम पद a तथा सार्वअन्तर d है।
तीसरा पद a₃ = a + (3 – 1)d = a + 2d
सातवाँ पद a₇ = a + (7 – 1)d = a + 6d
प्रश्नानुसार,
तीसरे और सातवें पदों का योग = 6
या a₃ + a₇ = 6
⇒ a + 2d + a + 6d = 6
⇒ 2a + 8d = 6
⇒ a + 4d = 3 …(1)
पुन: प्रश्नानुसार, a₃ × a₇ = 8
⇒ (a + 2d)(a + 6d) = 8
⇒ a² + 8ad + 12d² = 8 …(2)
समीकरण (1) के वर्ग में से समीकरण (2) को घटाने पर,
(a + 4d)² – (a² + 8ad + 12d²) = (3)² – 8
⇒ a² + 8ad + 16d² – a² – 8ad – 12d² = 9 – 8
4d² = 1
∴ d = ±\(\frac{1}{2}\)
तव a + 4d = 3 में d = \(\frac{1}{2}\) रखने पर,
a + 4 × \(\frac{1}{2}\) = 2
⇒ a + 2 = 3
∴ a = 1
पुन: a + 4d = 3 में d = –\(\frac{1}{2}\) रखने पर,
a + 4 × (-\(\frac{1}{2}\)) = 3
⇒ a – 2 = 3
∴ a = 5

स्थिति I. a = 1, d = \(\frac{1}{2}\)
प्रथम 16 पदों का योग
S₁₆ = \(\frac{16}{2}\) [2a + (16 – 1)d]
= 8[2 + 15 × \(\frac{1}{2}\)]
= 8 × \(\frac{19}{2}\) = 4 × 19 = 76
अतः 16 पदों का योग = 76

स्थिति II. a = 5, d = –\(\frac{1}{2}\)
∴ प्रथम 16 पदों का योग

अतः 16 पर्दों का योगफल = 20.

प्रश्न 3.
एक सीणी के क्रमागत डण्डे परस्पर 25 सेमी की दूरी पर हैं (देखिए आकृति)। डण्डों की लम्बाई एकसमान रूप से घटती जाती है तथा सबसे निचले डंडे की लम्बाई 45 सेमी है और सबसे ऊपर वाले डण्डे की लम्बाई 25 सेमी है। यदि ऊपरी और निचले डण्डे के बीच की दूरी 2\(\frac{1}{2}\) मीटर है, तो डण्डों को बनाने के लिए लकड़ी की कितनी लम्बाई की आवश्यकता होगी ?

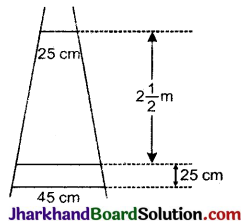
हल:
प्रथम व अन्तिम डण्डे के बीच की दूरी
= 2\(\frac{1}{2}\) मीटर = 250 सेमी
और दो क्रमागत डण्डों के बीच की दूरी = 25 सेमी
∴ सीणी में डण्डों की संख्या

∵ प्रथम डण्डे की लम्बाई (a) = 25 सेमी और अन्तिम डण्डे की लम्बाई (l) = 45 सेमी
∴ 11 डण्डों में प्रयुक्त लकड़ी की कुल माप
= 2\(\frac{1}{2}\)(a + l) = \(\frac{1}{2}\)(25 + 4)
\(\frac{11}{2}\) × 70 = 11 × 35
= 385 सेमी = 3.85 मीटर
अतः सीणी के डण्डों में प्रयुक्त लकड़ी की लम्बाई = 385 सेमी या 3.85 मीटर।

प्रश्न 4.
एक पंक्ति के मकानों को क्रमागत रूप से संख्या 1 से 49 तक अंकित किया गया है। दर्शाइए कि x का एक ऐसा मान है किx से अंकित मकान से पहले के मकानों की संख्याओं का योग उसके बाद वाले मकानों की संख्याओं के योग के बराबर है। x का मान ज्ञात कीजिए।
हल:
मकानों पर क्रमागत रूप से अंकित संख्याएँ :
1, 2, 3, 4, 5, 6, …… 47, 48, 49 है।
x एक ऐसी संख्या है कि x के एक ओर की संख्याओं का योग = x के दूसरी ओर की संख्याओं का योग
अर्थात् 1 से x – 1 तक की संख्याओं का योग
= x + 1 से 49 तक की संख्याओं का योग
अनुक्रम की सभी संख्याओं में सार्वअन्तर d = 1 है।
तब से x – 1 तक की संख्याओं का योग, a = 1, n = x – 1

और x + 1 से 49 तक की संख्याओं का योग
= S₄₉ – S_x
(∵ S_x+1 नहीं होगा क्योंकि x के बाद ही x + 1 प्रारम्भ होगा)

अतः x का मान 35 है।

प्रश्न 5.
एक फुटबाल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीणियाँ बनी हुई हैं। इन सीणियों में से प्रत्येक की लम्बाई 50 मीटर है और वह ठोस कंक्रीट (concrete) की बनी हैं। प्रत्येक सीणी में \(\frac{1}{4}\) मीटर की बनाई है और \(\frac{1}{2}\) मीटर का फैलाव (चौड़ाई) है। (देखिए आकृति)। इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।

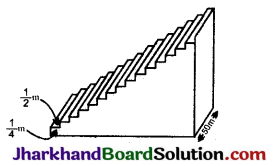
हल:
प्रत्येक सौणी की लम्बाई 50 मीटर और चौड़ाई \(\frac{1}{2}\) मीटर है सीणियों की संख्या 15 है। प्रत्येक सीणी की जमीन से ऊँचाई एक समान्तर श्रेढी (A.P.) का अनुक्रम है-
\(\frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \frac{4}{4}, \frac{5}{4}, \frac{6}{4}, \ldots, \frac{15}{4}\)
अतः पहली सीणी में लगी कंक्रीट का आयतन
= \(50 \times \frac{1}{2} \times \frac{1}{4}=\frac{50}{8}\) घन मीटर
दूसरी सीणी में लगी कंक्रीट का आयतन
= \(50 \times \frac{1}{2} \times \frac{2}{4}=\frac{100}{8}\) घन मीटर
तीसरी सीणी में लगी कंक्रीट का आयतन
\(=50 \times \frac{1}{2} \times \frac{3}{4}=\frac{150}{8}\) घन मीटर
चौथी सीणी में लगी कंक्रीट का आयतन
= \(50 \times \frac{1}{2} \times \frac{4}{4}=\frac{200}{8}\) घन मीटर
अतः चबूतरा बनाने में लगे कंक्रीट का कुल आयतन

अतः चबूतरे में लगी कंक्रीट का कुल आयतन = 750 घन मीटर