Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.2 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 6 त्रिभुज Exercise 6.2
प्रश्न 1.
आकृति (i) और (ii) में DE || BC है। (i) में, EC और (ii) में AD ज्ञात कीजिए।
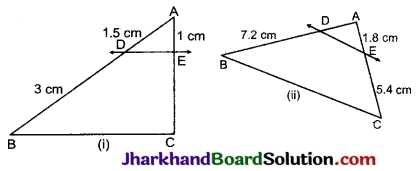
अथवा
यदि ΔABC में DE || BC है, AD = 1.5 सेमी, BD = 3 सेमी तथा AE = 1 सेमी हो, तो EC ज्ञात कीजिए।
हल:
(i) ΔABC में,
DE || BC (दिया है)
(आधारभूत समानुपातिक प्रमेय से)
\(\frac{A D}{D B}=\frac{A E}{E C}\)
⇒ \(\frac{1.5}{3}=\frac{1}{E C}\)
⇒ EC = \(\frac{3}{1.5}\)
∴ EC = 2 सेमी
(ii) ΔABC में,
DE || BC (आधारभूत समानुपातिक प्रमेय से)

![]()
प्रश्न 2.
किसी ΔPQR की भुजाओं PQ और PR पर क्रमशः बिन्दु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR है:
(i) PE = 3.9 सेमी, EQ = 3 सेमी, PF = 3.6 सेमी और FR = 2.4 सेमी।
(ii) PE = 4 सेमी, QE = 4.5 सेमी, PF = 8 सेमी और RF = 9 सेमी।
(iii) PQ = 1.28 सेमी, PR = 2.56 सेमी, PE = 0.18 सेमी और PF = 0.36 सेमी।
हल:
ΔPQR में दो बिन्दु E और F क्रमश: PQ और PR भुजाओं पर स्थित हैं।
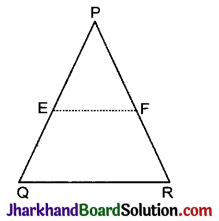
(i) PE = 3.9 सेमी, EQ = 3 सेमी, PF = 3.6 सेमी और FR = 2.4 सेमी,

अत: EF, QR के समान्तर नहीं है।
(ii) PE = 4 सेमी, QE = 4.5 सेमी, PF = 8 सेमी और RF = 9 सेमी,
\(\frac{P E}{Q E}=\frac{4}{4.5}=\frac{40}{45}=\frac{8}{9}\) …(1)
तथा \(\frac{P F}{R F}=\frac{8}{9}\) …(2)
समीकरण (1) व (2) से,
\(\frac{P E}{Q E}=\frac{P F}{R F}\)
(आधारभूत आनुपातिकता प्रमेय के विलोम से)
अत: EF || QR
(iii) PQ = 1.28 सेमी, PR = 2.56 सेमी, PE = 0.18 सेमी, PF = 0.36 सेमी
EQ = PQ – PE
= 1.28 – 0.18 = 1.10 सेमी
FR = PR – PF
= 2.56 – 0.36 = 2.20 सेमी

समीकरण (1) व (2) से,
\(\frac{P E}{E Q}=\frac{P F}{F R}\)
(आधारभूत आनुपातिकता प्रमेय के विलोम से)
अत: EF || QR
प्रश्न 3.
निम्न आकृति में, यदि LM || CB और LN || CD हो, तो सिद्ध कीजिए कि \(\frac{A M}{A B}=\frac{A N}{A D}\) है।
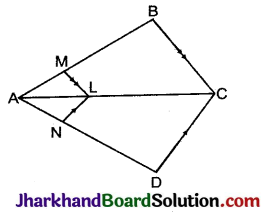
हल:
ΔABC में,
ML || BC (दिया है)
∴ \(\frac{A M}{M B}=\frac{A L}{L C}\) …(i)
(आधारभूत समानुपातिक प्रमेय से)
∴ पुन: ΔADC में,
LN || DC (दिया है)
\(\frac{A N}{N D}=\frac{A L}{L C}\) …(ii)
(आधारभूत आनुपातिकता प्रमेय से)
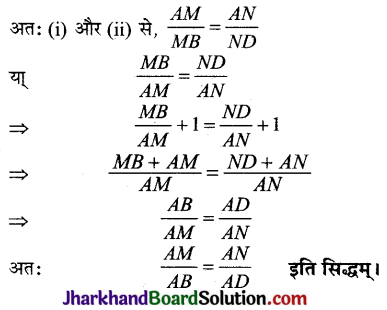
![]()
प्रश्न 4.
निम्न चित्र में, DE || AC और DF || AE है। सिद्ध कीजिए कि \(\frac{B F}{F E}=\frac{B E}{E C}\) है।
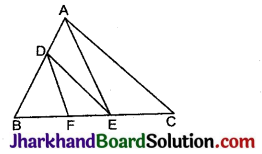
हल:
दिया है : ΔABC में भुजा AB पर एक बिन्दु D हैं और भुजा BC पर दो बिन्दु E व F हैं। रेखाखण्ड DF, DE व AE खींचे गये हैं।
सिद्ध करना है : \(\frac{B F}{F E}=\frac{B E}{E C}\)
उपपत्ति : ΔBCA में, DE || AC (दिया है)
∴ \(\frac{B E}{E C}=\frac{B D}{D A}\) …(i)
(आधारभूत समानुपातिक प्रमेय से)
पुन: ΔBEA में, DF || AE (दिया है)
∴ \(\frac{B F}{F E}=\frac{B D}{D A}\) …(ii)
(आधारभूत समानुपातिक प्रमेय से)
समीकरण (i) व (ii) से,
\(\frac{B F}{F E}=\frac{B E}{E C}\) इति सिद्धम्।
प्रश्न 5.
निम्न चित्र में, DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
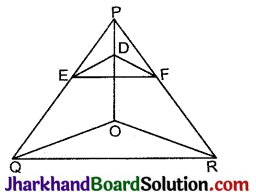
हल:
दिया है दी गई आकृति में DE || OQ तथा DF || OR है।
सिद्ध करना है : EF || QR
उपपत्ति : ΔPOQ में,
DE || OQ
\(\frac{P E}{E Q}=\frac{P D}{D O}\) …(i)
(आधारभूत आनुपातिकता प्रमेव से)
पुन: ΔPOR में,
DF || OR
\(\frac{P F}{F R}=\frac{P D}{D O}\) …(ii)
(आधारभूत आनुपातिकता प्रमेव से)
समीकरण (i) व (ii) से,
\(\frac{P E}{E Q}=\frac{P F}{F R}\)
अब ΔPQR में,
\(\frac{P E}{E Q}=\frac{P F}{F R}\)
(आधारभूत अनुपातिकता प्रमेय के विलोम से)
∴ EF || QR इति सिद्धम्।
प्रश्न 6.
निम्न चित्र में क्रमश: OP, OQ और OR पर स्थित बिन्दु A, B और C इस प्रकार हैं कि AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।
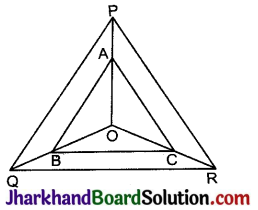
हल:
दिया है : ΔPQR में बिन्दु A, B और C क्रमश: OP, OQ और OR पर इस प्रकार स्थित हैं कि AB || PQ और AC || PR
सिद्ध करना है : BC || QR
उपपत्ति : ΔPQO में,
AB || PQ (दिया है)
\(\frac{O A}{A P}=\frac{O B}{B Q}\) …(i)
(आधारभूत समानुपातिक प्रमेय से)
पुन: ΔPRO में,
AC || PR
\(\frac{O A}{A P}=\frac{O C}{C R}\) …(ii)
(आधारभूत समानुपातिक प्रमेय से)
समीकरण (i) व (ii) से,
\(\frac{O B}{B Q}=\frac{O C}{C R}\)
(आधारभूत समानुपातिक प्रमेय के विलोम से)
ΔCQR में, BC || QR. इति सिद्धम्।
![]()
प्रश्न 7.
प्रमेय 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य बिन्दु से होकर दूसरी भुजा के समान्तर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है। (याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
हल:
दिया है : ΔABC में; D, AB का मध्य- बिन्दु है अर्थात् AD = DB है।
BC के समान्तर रेखा l, AB व AC को क्रमश: D तथा E बिन्दु पर प्रतिच्छेद करती है।
सिद्ध करना है : E, AC का मध्य- बिन्दु है।
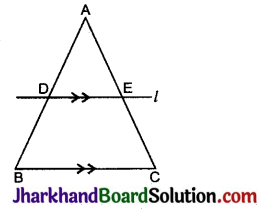
उपपत्ति: ∵ D, AB का मध्य बिन्दु है (दिया है)
∴ AD = DB
\(\frac{A D}{B D}=1\) …(i)
ΔABC में DE || BC
\(\frac{A D}{D B}=\frac{A E}{E C}\)
(आधारभूत समानुपातिक प्रमेय से)
\(1=\frac{A E}{E C}\)
[समी. (i) के प्रयोग से]
AE = EC
∴ E, AC का मध्यबिन्दु है। इति सिद्धम्।
प्रश्न 8.
प्रमेय 6.2 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के समान्तर होती है। (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके हैं।)
हल:
दिया है ΔABC में, AB तथा AC के मध्य-बिन्दु क्रमश: D और E हैं अर्थात् AD = BD और AE = EC हैं। D को E से मिलाया।
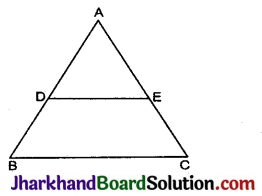
सिद्ध करना है: DE || BC
उपपत्ति D, AB का मध्य बिन्दु है
∴ AD = BD (दिया है)
⇒ \(\frac{A D}{B D}=1\) …(i)
E, AC का मध्य- बिन्दु है।
∴ AE = EC
⇒ \(\frac{A E}{E C}=1\) …(ii)
समीकरण (i) व (ii) से,
⇒ \(\frac{A D}{B D}=\frac{A E}{E C}\)
(आधारभूत समानुपातिकता प्रमेय के विलोम से)
∴ DE || BC इति सिद्धम्।
प्रश्न 9.
ABCD एक समलम्ब है जिसमें AB || DC है तथा इसके विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। दर्शाइए कि \(\frac{A O}{B O}=\frac{C O}{D O}\) हैं।
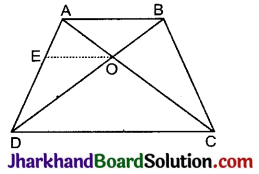
हल:
दिया है : समलम्ब चतुर्भुज ABCD है जिसमें AC और BD दो विकर्ण हैं, जो परस्पर O बिन्दु पर काटते हैं।
सिद्ध करना है : \(\frac{A O}{B O}=\frac{C O}{D O}\)
रचना : O से जाती हुई OE || CD खींची।
उपपत्ति: ΔADC में,
OE || DC
\(\frac{A E}{E D}=\frac{A O}{C O}\) …(i)
(आधारभूत समानुपातिक प्रमेय से)
समलम्ब चतुर्भुज ABCD में,
AB || CD
∴ OE || CD (रचना से)
OE || AB
अब ΔADB में,
OE || AB
\(\frac{E D}{A E}=\frac{D O}{B O}\)
⇒ \(\frac{A E}{E D}=\frac{B O}{D O}\) …(ii)
समीकरण (i) व समीकरण (ii) से,
\(\frac{A O}{C O}=\frac{B O}{D O}\)
⇒ AO × DO = BO × CO
⇒ \(\frac{A O}{B O}=\frac{C O}{D O}\) इति सिद्धम्।
![]()
प्रश्न 10.
एक चतुर्भुज ABCD के विकर्ण परस्पर हिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि \(\frac{A O}{B O}=\frac{C O}{D O}\) है। दर्शाइए कि ABCD एक समलम्ब है।
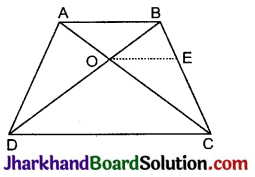
हल:
दिया है ABCD एक चतुर्भुज है जिसके विकर्णं AC तथा BD बिन्दु O पर एक दूसरे को इस प्रकार प्रतिच्छेद करते हैं कि
\(\frac{A O}{B O}=\frac{C O}{D O}\)
सिद्ध करना है : ABCD एक समलम्ब है।
रचना : O से OE || DC खींची।
उपपत्ति: ΔBDC में,
OE || DC
\(\frac{B O}{D O}=\frac{B E}{E C}\) …(i)
परन्तु दिया है, \(\frac{A O}{B O}=\frac{C O}{D O}\)
⇒ \(\frac{A O}{C O}=\frac{B O}{D O}\) … (ii)
समीकरण (i) व (ii) से,
\(\frac{A O}{C O}=\frac{B E}{E C}\)
⇒ \(\frac{C O}{A O}=\frac{E C}{B E}\)
∴ OE || AB
(आधारभूत आनुपातिक प्रमेय के विलोम से)
इसी प्रकार, OE || CD
⇒ AB || CD
अत: ABCD एक समलम्ब है। इति सिद्धम्।