JAC Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.3

Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 6 त्रिभुज Exercise 6.3

प्रश्न 1.
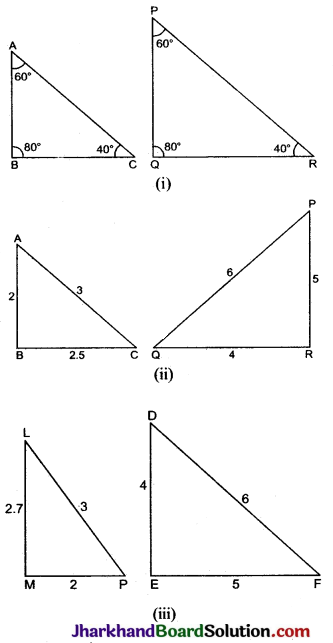
बताइए कि निम्न आकृतियों में दए गए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।


हल:
(i) ΔABC तथा ΔPQR में,
∠A = ∠P (प्रत्येक 60°)
∠B = ∠Q (प्रत्येक 80°)
∠C = ∠R (प्रत्येक 40°)
A-A-A समरूपता कसौटी से,
ΔABC ~ ΔPQR

(ii) ΔABC तथा ΔQRP में,

S-S-S समरूपता कसौटी से,
ΔABC ~ ΔQRP

(iii) ΔLMP तथा ΔDEF में,
\(\frac{M P}{D E}=\frac{2}{4}=\frac{1}{2}\)
\(\frac{P L}{D F}=\frac{3}{6}=\frac{1}{2}\)
\(\frac{L M}{E F}=\frac{2.7}{5}=\frac{27}{50}\)
यहाँ \(\frac{M P}{D E}=\frac{P L}{D F} \neq \frac{L M}{E F}\)
∵ दोनों त्रिभुजों की भुजाएँ समानुपात में नहीं हैं।
∴ दोनों त्रिभुज समरूप नहीं हैं।

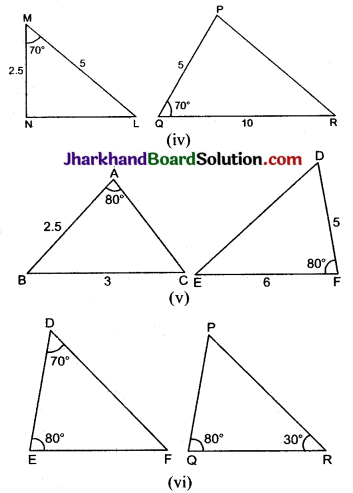
(iv) ΔMNL तथा ΔQPR में,
\(\frac{M L}{Q R}=\frac{5}{10}=\frac{1}{2}\)
∠M = ∠Q = 70°
\(\frac{M N}{P Q}=\frac{2.5}{5}=\frac{1}{2}\)
S-A-S समरूपता कसौटी से,
ΔMNL ~ ΔQPR

(v) ΔABC तथा ΔDEF में,
\(\frac{A B}{D F}=\frac{2.5}{5}=\frac{1}{2}\)
\(\frac{B C}{E F}=\frac{3}{6}=\frac{1}{2}\)
∠B ≠ ∠F [∵ ∠B अज्ञात है]
अतः दोनों त्रिभुज समरूप नहीं हैं।

(vi) ΔDEF में,
∠D = 70°, ∠E = 80°
∵ ∠D + ∠E + ∠F = 180°
∴ 70° + 80° + ∠F = 180°
⇒ ∠F = 180° – 70° – 80°
∴ ∠F = 30°
ΔPQR में, ∠Q = 80°, ∠R = 30°
∵ ∠P + ∠Q + ∠R = 180°
⇒ ∠P + 80° + 30° = 180°
⇒ ∠P = 180° – 80° – 30°
∴ ∠P = 70°
ΔDEF एवं ΔPQR से,
∠D = ∠P (प्रत्येक 70°)
∠E = ∠Q (प्रत्येक 80°)
∠F = ∠R (प्रत्येक 30°)
A-A-A समरूपता कसौटी में,
ΔDEF ~ ΔPQR.

प्रश्न 2.
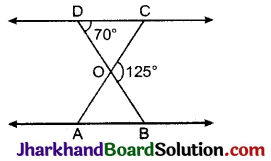
निम्न आकृति में, ΔODC ~ ΔOBA, ∠BOC = 125° और ∠CDO = 70° है। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।

हल:
∠BOC = 125°
∠CDO = 70°
∵ DOB एक सरल रेखा है।
∴ ∠DOC + ∠COB = 180°
⇒ ∠DOC = ∠180° – ∠COB
⇒ ∠DOC = 180° – 125°
∴ ∠DOC = 55°
अतः ∠DOC = ∠AOB = 55° (शीर्षाभिमुख कोण)

ΔDCO में,
∠D + ∠O + ∠C = 180°
⇒ 70° + 55° + ∠C = 180°
⇒ ∠C = 180° – 70° – 55°
∴ ∠C = 55°
अर्थात् ∠DCO = 55°
∵ ΔODC ~ ΔOBA (दिया है)
∴ ∠DCO = ∠OAB
(∵ दो समरूप त्रिभुज के संगत कोण बराबर होते हैं)
∠OAB = 55°
अतः ∠DOC = 55°
∠DCO = 55°
और ∠OAB = 55°

प्रश्न 3.
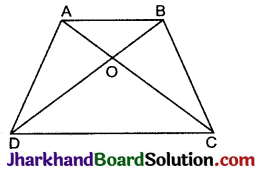
समलम्ब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि \(\frac{O A}{O C}=\frac{O B}{O D}\) है।

हल:
दिया है: ABCD एक समलम्ब है जिसमें AB || CD तथा उसके विकर्ण AC और BD बिन्दु O पर काटते हैं।
सिद्ध करना है: \(\frac{O A}{O C}=\frac{O B}{O D}\)
उपपत्ति: AB || CD और AC तिर्यक रेखा है।
∠OAB = ∠OCD (एकान्तर कोण युग्म)
और ∠AOB = ∠COD (शीर्षाभिमुख कोण)
अब ΔAOB और ΔCOD में,
∠OAB = ∠OCD तथा ∠AOB = ∠COD
त्रिभुजों की समरूपता के उपगुणधर्म A-A से,
ΔAOB ~ ΔCOD
∴ \(\frac{O A}{O C}=\frac{O B}{O D}\)
(भुजाओं की आनुपातिकता से) इति सिद्धम्।

प्रश्न 4.
आकृति में \(\frac{Q R}{Q S}=\frac{Q T}{P R}\) तथा ∠1 = ∠2 है। दर्शाइए कि ΔPQS ~ ΔTQR है।

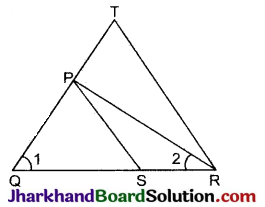
हल:
दिया है: दी गई आकृति में,
\(\frac{Q R}{Q S}=\frac{Q T}{P R}\) तथा ∠1 = ∠2
सिद्ध करना है: ΔPQS ~ ΔTQR
उपपत्ति: ΔPQR में,
∠1 = ∠2 (दिया है)
∴ PR = PQ
(बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं)

S-A-S समरूपता कसौटी से,
ΔPQS ~ ΔTQR इति सिद्धम्।

प्रश्न 5.
ΔPQR की भुजाओं PR और OR पर क्रमशः बिन्दु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ΔRPQ ~ ΔRTS है।

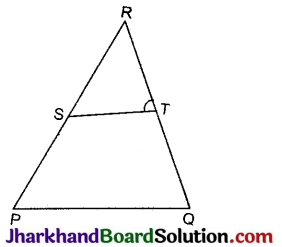
हल:
दिया है: ΔPQR की भुजाओं PR और OR पर क्रमश: S तथा T बिन्दु इस प्रकार स्थित हैं कि ∠P = ∠RTS है।
सिद्ध करना है: ΔRPQ ~ ΔRTS
उपपत्ति: ΔRPQ और ΔRTS में,
∠P = ∠RTS
तथा ∠R = ∠R (उभयनिष्ठ)
त्रिभुजों की समरूपता के उपगुणधर्म AA से
ΔRPQ ~ ΔRTS इति सिद्धम्।

प्रश्न 6.
दी गई आकृति में, यदि ΔABE ≅ ΔACD है, तो दर्शाइए कि ΔADE ~ ΔABC है।

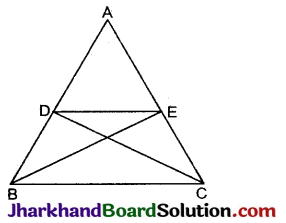
हल:
दिया है: दी गई आकृति में ΔABE ≅ ΔACD है।
सिद्ध करना है: ΔADE ~ ΔABC
उपपत्ति: ΔABE ≅ ΔACD (दिया है)
AB = AC
(सर्वांगसम त्रिभुजों की संगत भुजाएँ)
और AE = AD
(सर्वांगसम त्रिभुजों की संगत भुजाएँ)
\(\frac{A B}{A C}=1\) …(i)
तथा \(\frac{A D}{A E}=1\) …(ii)
समीकरण (i) व समीकरण (ii) से,
\(\frac{A B}{A C}=\frac{A D}{A E}\) ⇒ \(\frac{A D}{A B}=\frac{A E}{A C}\)
ΔADE और ΔABC में,
\(\frac{A D}{A B}=\frac{A E}{A C}\)
∠A = ∠A (उभयनिष्ठ)
S-A-S समरूपता कसौटी से,
ΔADE ~ ΔABC इति सिद्धम्।

प्रश्न 7.
आकृति में, ΔABC के शीर्षलम्ब AD और CE परस्पर बिन्दु P पर प्रतिच्छेद करते हैं दर्शाइए कि :

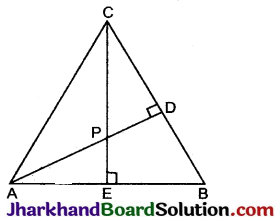
(i) ΔAEP ~ ΔCDP
(ii) ΔABD ~ ΔCBE
(iii) ΔAEP ~ ΔADB
(iv) ΔPDC ~ ΔBEC
हल:
दिया है: ΔABC में AD और CE शीर्ष लम्ब हैं, जो बिन्दु P पर काटते हैं।
सिद्ध करना है: (i) ΔAEP ~ ΔCDP
(ii) ΔABD ~ ΔCBE
(iii) ΔAEP ~ ΔADB
(iv) ΔPDC ~ ΔBEC
उपपत्ति: (i) ΔAEP और ΔCDP में,
∠E = ∠D (प्रत्येक 90°)
∠APE = ∠CPD (शीर्षाभिमुख कोण)
A-A समरूपता कसौटी से,
ΔAEP ~ ΔCDP

(ii) ΔABD और ΔCBE में,
∠D = ∠E (प्रत्येक 90°)
∠B = ∠B (उभयनिष्ठ)
A-A समरूपता कसौटी से,
ΔABD ~ ΔCBE

(iii) ΔAEP और ΔADB में,
∠E = ∠D (प्रत्येक 90°)
∠A = ∠A (उभयनिष्ठ)
A-A समरूपता कसौटी से,
ΔAEP ~ ΔADB

(iv) ΔPDC और ΔBEC में,
∠C = ∠C (उभयनिष्ठ)
∠D = ∠E (प्रत्येक 90°)
A-A समरूपता कसौटी से,
ΔPDC ~ ΔBEC इति सिद्धम्।

प्रश्न 8.
समान्तर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिन्दु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ΔABE ~ ΔCFB है।
हल:
दिया है: समान्तर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिन्दु हैं तथा BE भुजा CD को F बिन्दु पर प्रतिच्छेद करती है।
सिद्ध करना है: ΔABE ~ ΔCFB

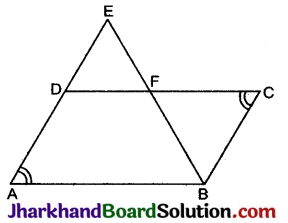
उपपत्ति: ΔABE और ΔCFB में,
∠A = ∠C
(समान्तर चतुर्भुज के सम्मुख कोण)
∵ AE || BC
तथा BE तिर्यक् रेखा है।
∠AEB = ∠CBF (एकान्तर कोण)
A-A समरूपता कसौटी से,
ΔABE ~ ΔCFB इति सिद्धम्।

प्रश्न 9.
निम्न आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि:

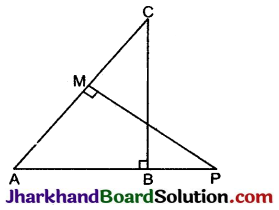
(i) ΔABC ~ ΔAMP
(ii) \(\frac{C A}{P A}=\frac{B C}{M P}\)
हल:
दिया है:
ΔABC और ΔAMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं।
सिद्ध करना है:
(i) ΔABC ~ ΔAMP
(ii) \(\frac{C A}{P A}=\frac{B C}{M P}\)
उपपत्ति: (i) ΔABC और ΔAMP में,
∠A = ∠A (उभनिष्ठ)
∠B = ∠M (प्रत्येक 90°)
A-A समरूपता कसौटी से,
ΔABC ~ ΔAMP

(ii) ∵ ΔABC और ΔAMP समरूप त्रिभुज है।
∴ \(\frac{A C}{P A}=\frac{B C}{M P}\)
(यदि दो त्रिभुज समरूप हों तो उनकी संगत भुजाएँ समानुपाती होती हैं)
अतः \(\frac{C A}{P A}=\frac{B C}{M P}\) इति सिद्धम्।

प्रश्न 10.
CD और GH क्रमश: ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं। यदि ΔABC ~ ΔFEG है, तो दर्शाइए कि :

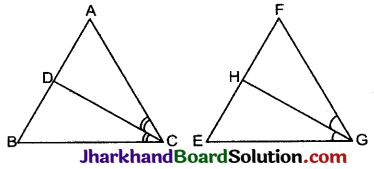
(i) \(\frac{C D}{G H}=\frac{A C}{F G}\)
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGE
हल:
दिया है: ΔABC तथा ΔFEG में, ZACB तथा ZEGF के समद्विभाजक CD तथा GH इस प्रकार है कि D, AB पर तथा H, FE पर स्थित है।
तथा ΔABC ~ ΔFEG
(i) ∵ ΔABC ~ ΔFEG
∴ ∠CAB = ∠GEF
⇒ ∠CAD = ∠GFH …(i)
और ∠ACB = ∠FGE
⇒ \(\frac{1}{2}\)∠ACB = \(\frac{1}{2}\)∠FGE
⇒ ∠ACD = ∠FGH …(ii)
समीकरण (i) व (ii) से
ΔACD ~ ΔFGH (AA समरूपता से)
∵ दो समरूप त्रिभुजों की संगत गुजाएँ समानुपात में होती हैं।
अतः \(\frac{C D}{G H}=\frac{A C}{F G}\)

(ii) ∵ ΔABC ~ ΔFEG
∴ ∠ABC = ∠FEG
⇒ ∠DBC = ∠HEG …(iii)
और ∠ACB = ∠FGE
⇒ \(\frac{1}{2}\)∠ACB = \(\frac{1}{2}\)∠FGE
ΔDCB = ΔHGE … (iv)
समीकरण (iii) और (iv) से,
ΔDCB ~ ΔHGE (AA समरूपता से)

(iii) ∵ ΔABC ~ ΔFEG
∴ ∠CAB = ∠GFE
⇒ ∠CAD = ∠GFH
⇒ ∠DAC = ∠HFG ….(v)
और ∠ACB = ∠FGE
⇒ \(\frac{1}{2}\)∠ACB = \(\frac{1}{2}\)∠FGE
⇒ ∠DCA = ∠HGF …(vi)
समीकरण (v) और (vi) से,
ΔDCA ~ ΔHGF (AA समरूपता से)

प्रश्न 11.
निम्न आकृति में, AB = AC वाले एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिन्दु है। यदि AD ⊥ BC और EF ⊥ AC है, तो सिद्ध कीजिए कि ΔABD ~ ΔECF है।

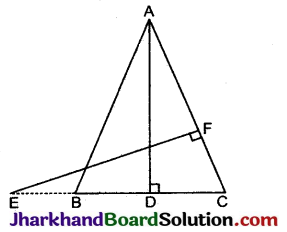
हल:
दिया है: एक समद्विबाहु त्रिभुज ABC है, जिसमें AB = AC है तथा CB को E बिन्दु तक इस प्रकार बढ़ाया गया है कि EF ⊥ AC और AD ⊥ BC है।
सिद्ध करना है: ΔABD ~ ΔECF
उपपत्ति: ΔABC एक समद्विबाहु त्रिभुज है। (दिया है)
∴ AB = AC
तथा ∠B = ∠C
(त्रिभुज में समान भुजाओं के सम्मुख कोण बराबर होते हैं)
अब ΔABD और ΔECF में,
∠ABD = ∠ECF (ऊपर सिद्ध किया है)
∠ADB = ∠EFC (प्रत्येक 90°)
∴ A-A समरूपता कसौटी से,
ΔABD ~ ΔECF इति सिद्धम्।

प्रश्न 12.
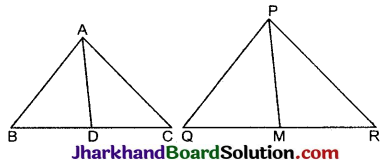
एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती हैं ΔABC ~ ΔPQR है।

हल:
दिया है:
ΔABC तथा ΔPQR दो त्रिभुज हैं जिनमें AD तथा PM माध्यिकाएँ हैं,
अर्थात् BD =\(\frac{1}{2}\)BC तथा QM = \(\frac{1}{2}\)QR
तथा \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A D}{P M}\) है …(i)
सिद्ध करना है: ΔABC और ΔPQR समरूप हैं।
उपपत्ति: \(\frac{B C}{Q R}=\frac{A D}{P M}\) (दिया है)
\(\frac{2 B D}{2 Q M}=\frac{A D}{P M}\)
[∵ BD = \(\frac{1}{2}\)BC तथा QM = \(\frac{1}{2}\)QR]
\(\frac{B D}{Q M}=\frac{A D}{P M}\) … (ii)
अब ΔABD तथा PQM में,
समी. (i) व (ii) से,
\(\frac{A B}{P Q}=\frac{B D}{Q M}=\frac{A D}{P M}\)
ΔABD ~ ΔPQM
∴ ∠B = ∠Q
ΔABC तथा ΔPQR में,
\(\frac{A B}{P Q}=\frac{B C}{Q R}\) [समी. (i) से]
∠B = ∠Q
∴ S-A-S समरूपता कसौटी से,
ΔABC ~ ΔPQR इति सिद्धम्।

प्रश्न 13.
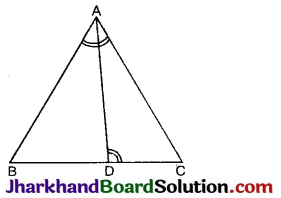
एक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA² = CB.CD है।

हल:
दिया है: ΔABC की भुजा BC पर एक बिन्दु D इस प्रकार है कि ∠ADC = ∠BAC
सिद्ध करना है: CA² = CB × CD
उपपत्ति: ΔABC और ΔDAC में,
∠C = ∠C (उभयनिष्ठ)
∠BAC = ∠ADC (दिया है)
∴ A-A समरूपता कसौटी से,
ΔABC ~ ΔDAC
\(\frac{A C}{D C}=\frac{B C}{\dot{A C}}\)
(यदि दो त्रिभुज समरूप हों तो उनकी भुजाएँ समानुपाती होती हैं)
∴ AC² = BC.DC
या AC² = CB.CD इति सिद्धम्।

प्रश्न 14.
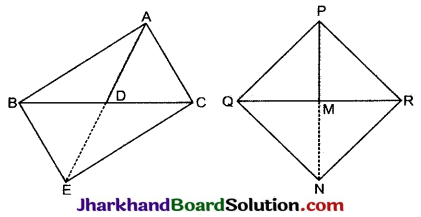
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ΔABC ~ ΔPQR है।

हल:
दिया है: दो त्रिभुज ABC और POR में, D, BC का मध्य-बिन्दु है और QR का मध्य- बिन्दु M है।
तथा \(\frac{A B}{P Q}=\frac{A C}{P R}=\frac{A D}{P M}\) …(i)
सिद्ध करना है:
ΔABC ~ ΔPQR
रचना: AD को E तक इस प्रकार बढ़ाया कि AD = DE हो। BE और CE को मिलाया तथा PM को N तक इस प्रकार बढ़ाया कि PM = MN हो। QN और NR को मिलाया।
उपपत्ति: चतुर्भुज ABEC के विकर्ण AE और BC परस्पर D बिन्दु पर समद्विभाजित करते हैं।
∴ चतुर्भुज ABEC एक समान्तर चतुर्भुज है।
∴ BE = AC …(ii)
इसी प्रकार PQNR भी एक समान्तर चतुर्भुज है।
∴ QN = PR …(iii)
समीकरण (ii) को (iii) से विभाजित करने पर,
\(\frac{B E}{Q N}=\frac{A C}{P R}\) …(iv)
अब \(\frac{A D}{P M}=\frac{2 A D}{2 P M}=\frac{A D}{P M}=\frac{A E}{P N}\) …(v)
समीकरण (i), (iv) और (v) में,
\(\frac{A B}{P Q}=\frac{B E}{Q N}=\frac{A E}{P N}\)
अत: ΔABE और ΔPQN मैं,
\(\frac{A B}{P Q}=\frac{B E}{Q N}=\frac{A E}{P N}\)
∴ ΔABE ~ ΔPQN (SSS से)
∴ ∠BAE = ∠QPN …(vi)
इसी प्रकार,
ΔAEC ~ ΔPNR
∴ ∠EAC = ∠NPR …(vii)
समीकरण (vi) व (vii) को जोड़ने पर,
∠BAE + ∠EAC = ∠QPN + ∠NPR
⇒ ∠BAC = ∠QPR
अब ΔABC और ∠PQR में,
\(\frac{A B}{P Q}=\frac{A C}{P R}\) [समी. (i) से]
∠A = ∠P
S-A-S समरूपता कसौटी से,
ΔABC ~ ΔPQR इति सिद्धम्।

प्रश्न 15.
6 मीटर लम्बाई वाले एक ऊर्ध्वाधर स्तम्भ की भूमि पर छाया की लम्बाई 4 मीटर है, जबकि उसी समय एक मीनार की छाया की लम्बाई 28 मीटर है। मीनार की ऊँचाई ज्ञात कीजिए।
हल:
दिया है: 6 मीटर लम्बे स्तम्भ CD की छाया DE = 4 मीटर प्राप्त होती है। उसी समय एक मीनार AB जिसकी ऊँचाई माना h मीटर है की छाया BE = 28 मीटर प्राप्त होती है।
ज्ञात करना है: मीनार AB की ऊँचाई (h)।

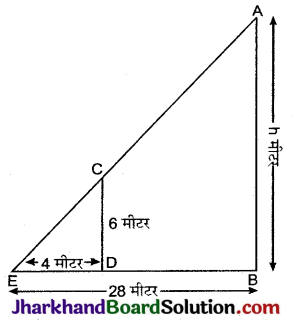
गणना : ΔABE और ΔCDE समरूप हैं।
∴ \(\frac{A B}{C D}=\frac{B E}{D E}\)
⇒ \(\frac{h}{6}=\frac{28}{4}\)
⇒ h = \(\frac{28}{4}\) × 6
∴ h = 42 मीटर
अत: मीनार की ऊँचाई = 42 मीटर

प्रश्न 16.
AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ΔABC ~ ΔPQR है।
सिद्ध कीजिए कि \(\frac{A B}{P Q}=\frac{A D}{P M}\) है।
हल:
दिया है: ΔABC और ΔPQR समरूप त्रिभुज हैं जिनमें AD और PM क्रमश: ΔABC और ΔPQR की माध्यिकाएँ हैं।

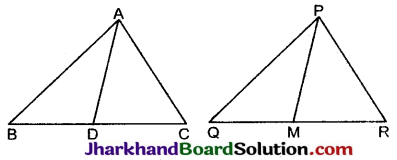
सिद्ध करना है: \(\frac{A B}{P Q}=\frac{A D}{P M}\)
उपपत्ति: ΔABC और ΔPQR समरूप हैं।
\(\frac{A B}{P Q}=\frac{B C}{Q R}\) …(i)
∠Q = ∠B (ΔABC ~ ΔPQR)
∵ AD, ΔABC की माध्यिका है।
∴ BD = \(\frac{1}{2}\)BC ⇒ BC = 2BD
तथा PM, ΔPQR की माध्यिका है।
∴ QM = \(\frac{1}{2}\)QR ⇒ QR = 2QM
समीकरण (i) से,
\(\frac{A B}{P Q}=\frac{2 B D}{2 Q M}\)
⇒ \(\frac{A B}{P Q}=\frac{B D}{Q M}\) …(ii)
अब ΔABD और ΔPQM की तुलना करने पर,
\(\frac{A B}{P Q}=\frac{B D}{Q M}\)
∠B = ∠Q
∴ S-A-S समरूपता कसौटी से,
ΔΑΒD ~ ΔΡQΜ
\(\frac{A B}{P Q}=\frac{A D}{P M}\)
(समरूप त्रिभुजों की संगत भुजाएँ समानुपातिक होती हैं) इति सिद्धम्।