Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 Triangles Ex 6.5 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 6 Triangles Exercise 6.5
Question 1.
Sides of triangles are given below, Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse:
1. 7 cm, 24 cm, 25 cm
2. 3 cm, 8 cm, 6 cm
3. 50 cm, 80 cm, 100 cm
4. 13 cm, 12 cm, 5 cm
Solution :
1. 7 cm, 24 cm, 25 cm.
Here, the longest side is 25 cm.
25² = 625 and 7² + 24² = 49 + 576 = 625
∴ 25² = 7² + 24²
Here, the square of the longest side equals the sum of squares of the other two sides. Hence, the triangle with sides 7 cm, 24 cm and 25 cm is a right triangle and the length of its hypotenuse, is 25 cm.
2. 3 cm, 8 cm, 6 cm
Here, the longest side is 8 cm.
8² = 64 and 3² + 6² = 9 + 36 = 45
∴ 8² ≠ 3² + 6²
Hence, the triangle with sides 3 cm, 8 cm and 6 cm is not a right triangle.
3. 50 cm, 80 cm, 100 cm
Here, the longest side is 100 cm.
100² = 10000 and
50² + 80² = 2500 + 6400 = 8900
∴ 100² ≠ 50² + 80²
Hence, the triangle with sides 50 cm, 80 cm and 100 cm is not a right triangle.
4. 13 cm, 12 cm, 5 cm
Here, the longest side is 13 cm.
13² = 169 and 12² + 5² = 144 + 25 = 169
∴ 13² = 12² + 5²
Here, the square of the longest side equals the sum of squares of the other two sides. Hence, the triangle with sides 13 cm. 12 cm and 5 cm is a right triangle and the length of its hypotenuse is 13 cm.
![]()
Question 2.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM. MR.
Solution :
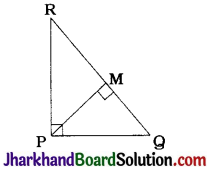
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR.
∴ ΔRMP ~ ΔPMQ ~ ΔRPQ (Theorem 6.7)
Now, ΔRMP ~ ΔPMQ
∴ \(\frac{PM}{QM}=\frac{RM}{PM}\)
∴ PM² = QM. MR
Question 3.
In the given figure, ABD is a triangle right-angled at A and AC ⊥ BD. Show that
1. AB² = BC.BD
2. AC² = BC.DC
3. AD² = BD.CD
Solution :
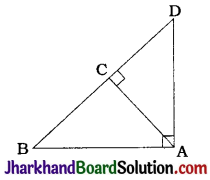
ABD is a triangle right angled at A and AC ⊥ BD.
∴ ΔBCA ~ ΔACD ~ ΔBAD (Theorem 6.7)
1. ΔBCA ~ ΔBAD
∴ \(\frac{AB}{DB}=\frac{CB}{AB}\)
∴ AB² = BC. BD
2. ΔBCA ~ ΔACD
∴ \(\frac{AC}{DC}=\frac{BC}{AC}\)
∴ AC² = BC. DC
3. ΔACD ~ ΔBAD
∴ \(\frac{AD}{BD}=\frac{CD}{AD}\)
∴ AD² = BD . CD
Question 4.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².
Solution :
ABC is an isosceles triangle right angled at C.
Hence, AB is the hypotenuse and the other two sides are equal, i.e., BC = AC
In ΔABC, ∠C = 90°
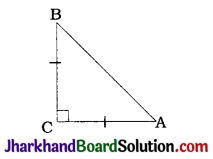
∴ By Pythagoras theorem,
AB² = BC² + AC²
∴ AB² = AC² + AC² (∵ BC = AC)
∴ AB² = 2AC²
![]()
Question 5.
ABC is an isosceles triangle with AC = BC. If AB² = 2AC², prove that ABC is a right triangle.
Solution :
In ΔABC, AC = BC and AB² = 2AC²
AB² = 2AC²
∴ AB² = AC² + AC²
∴ AB² = AC² + BC² (∵ AC = BC)
Hence, by the converse of Pythagoras theorem, ΔABC is right triangle in which ∠C is a right angle.
Question 6.
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution :
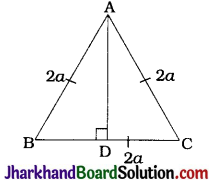
In ΔABC, AB = BC = CA = 2a.
Let AD be its altitude
∴ ∠ADB = ∠ADC = 90°
In ΔADB and ΔADC,
∠ADB = ∠ADC = 90°
AB = AC
AD = AD
∴ By RHS criterion,
= ΔADC
∴ BD = CD
But, BD + CD = BC
∴ BD = CD = \(\frac{1}{2}\)BC = \(\frac{1}{2}\)(2a) = a
Now, in ΔADB, ∠D = 90°
∴ By Pythagoras theorem,
AB² = AD² + BD²
∴ (2a)² = AD² + (a)²
∴ 4a² – a² = AD²
∴ AD² = 3a²
∴ AD = \(\sqrt{3}\)a
All the altitudes of an equilateral triangle are equal.
Hence, each of the altitudes of equilateral ΔABC with side 2a is \(\sqrt{3}\)a.
Question 7.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Solution :
Given: ABCD is a rhombus.
To prove : AB² + BC² + CD² + DA² = AC² + BD²
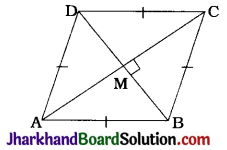
Proof: ABCD is a rhombus.
∴ AB = BC = CD = DA ……………(1)
Let its diagonals AC and BD intersect at M.
Then, MA = MC = \(\frac{1}{2}\)AC.
MB = MD = \(\frac{1}{2}\)BD and
∠AMB = ∠BMC = ∠CMD = ∠DMA = 90°
In ΔAMB, ∠AMB = 90°
∴ AB² = MA² + MB² (Pythagoras theorem)
∴ AB² = (\(\frac{AC}{2}\))² + (\(\frac{BD}{2}\))²
∴ AB² = (\(\frac{AC}{2}\))² + (\(\frac{BD}{2}\))²
∴ 4AB² = \(\frac{\mathrm{AC}^2}{4}+\frac{\mathrm{BD}^2}{4}\)
∴ 4AB² = AC² + BD²
∴ AB² + AB² + AB² + AB² = AC² + BD²
∴ AB² + BC² + CD² + DA² = AC² + BD²
![]()
Question 8.
In the given figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:
1. OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
2. AF² + BD² + CE² = AE² + CD² + BF².
Solution :
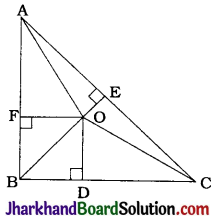
Join OA, OB and OC.
Here, in ΔOFA and ΔOFB, ∠F = 90°, in ΔODB and ΔODC, ∠D = 90° and in ΔOEC and ΔOEA. ∠E = 90°.
Then, Pythagoras theorem is applicable in all the triangles.
1. In ΔOFA, ∠F = 90°
∴ OA² = OF² + AF²
∴ AF² = OA² – OF² …………..(1)
In ΔODB, ∠D = 90°
∴ OB² = OD² + BD²
∴ BD² = OB² – OD² …………..(2)
In ΔOEC, OE² + CE²
∴ CE² = OC² – OE² …………..(3)
Adding (1), (2) and (3).
AF² + BD² + CE² = OA² – OF² + OB² – OD² + OC² – OE²
∴ OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
2. AF² + BD² + CE² = OA² + OB² + OC² – OD² – OE² – OF²
∴ AF² + BD² + CE² = (OA² – OE²) + (OB² – OF²) + (OC² – OD²)
∴ AF² + BD² + CE² = AE² + BF² + CD² (∵ ΔOAE, ΔOBF and ΔOCD are right triangles)
∴ AF² + BD² + CE² = AE² + CD² + BF²
Question 9.
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Solution :
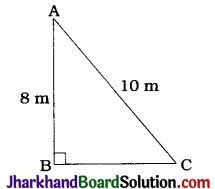
Here, AB is the wall with window at point A and AC is the ladder.
Then, AC = 10m and AB = 8 m.
In ΔABC, ∠B = 90°.
∴ AC² = AB² + BC² (Pythagoras theorem)
∴ 10² = 8² + BC²
∴ BC² = 10² – 8²
∴ BC² = 100 – 64
∴ BC² = 36
∴ BC = 6 m
Thus, the distance of the foot of the ladder from the base of the wall is 6 m.
Question 10.
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution :
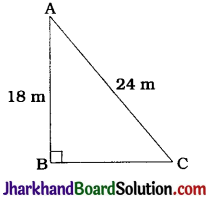
Here, AB is the vertical pole in which the guy wire is attached at point A and AC is the guy wire and 18 m the stake is attached to its end C.
Then, AC = 24 m and AB = 18 m.
In ΔABC, ∠B = 90°
∴ AC² = AB² + BC² (Pythagoras theorem)
∴ 24² = 18² + BC²
∴ BC² = 576 – 324
∴ BC² = 252
∴ BC² = 4 × 9 × 7
∴ BC = 2 × 3 × \(\sqrt{7}\)
∴ BC = 6\(\sqrt{7}\) m
Thus, the stake should be driven 6\(\sqrt{7}\)m far from the base of the pole, so as to make the wire taut.
![]()
Question 11.
An airplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another airplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1\(\frac{1}{2}\) hours?
Solution :
Here, A is the airport, B is the position of the first plane flying due north after 1\(\frac{1}{2}\) hours and C is the position of the second c- plane flying due west after 1\(\frac{1}{2}\) hours.
[Note: For the sake of simplicity, we consider that both the planes are flying at the same height and point A representing the airport is also imagined to be at the same height.]
Then, AB = distance covered by the first plane in 1\(\frac{1}{2}\) hours
= Speed × Time
= 1000 × \(\frac{3}{2}\)
= 1500 km
Similarly, AC = distance covered by the second plane in 1\(\frac{1}{2}\) hours
= Speed × Time
= 1200 × \(\frac{3}{2}\)
= 1800 km
Also, ∠BAC is the angle formed by north direction and west direction.
Hence ∠BAC = 90°
Now, in ΔABC, ∠A = 90°
∴ BC² = AB² + AC² (Pythagoras theorem)
∴ BC² = (1500)² + (1800)²
∴ BC² = 22500 + 32400
∴ BC² = 54900
∴ BC = \(\sqrt{100 \times 9 \times 61}\)
∴ BC = 300\(\sqrt{61}\) km
Thus, the two planes will be 300\(\sqrt{61}\) km apart from each other after 1\(\frac{1}{2}\) hours.
Question 12.
Two poles of heights 6m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution :
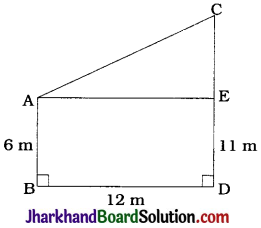
Here, AB and CD are two erect poles of height 6 m and 11 m respectively.
The distance between the feet of the poles is 12 m.
Then, AB = 6 m, BD = 12 m, CD = 11 m, ∠B = 90° and ∠D = 90°.
Draw AE || BC.
Then, in quadrilateral ABDE.
∠B = ∠D = ∠E = ∠A = 90°.
Hence, ABDE is a rectangle.
∴ ED = AB = 6m and AE = BD = 12 m.
Then, CE = CD – DE = 11 – 6 = 5m
Now, in ΔAEC, ∠E = 90°.
∴ AC² = AE² + CE² (Pythagoras theorem)
∴ AC² = 12² + 5²
∴ AC² = 144 + 25
∴ AC² = 169
∴ AC = 13 m
Thus, the distance between the tops of the vertical poles is 13 m.
![]()
Question 13.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE²
Solution :
In ΔABC, ∠C is a right angle, point D lies on CA and point E lies on CB.
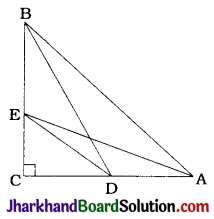
Then, all the four triangles BCD, BCA, ECD and ECA are right triangles and in each of them C is a right angle.
Hence, Pythagoras theorem is applicable in all the four triangles.
In ΔECA, AE² = EC² + CA² ……………..(1)
In ΔBCD, BD² = BC² + CD² ……………..(2)
In ΔBCA, AB² = BC² + CA² ……………..(3)
In ΔECD, DE² = EC² + CD² ……………..(4)
Adding (1) and (2).
AE² + BD² = EC² + CA² + BC² + CD²
= (BC² + CA²) + (EC² + CD²)
= AB² + DE² [By (3) and (4)]
Thus, AE² + BD² = AB² + DE²
Question 14.
The perpendicular from A on side BC of a ΔABC intersects BC at D such that DB = 3CD (see the given figure). Prove that 2AB² = 2AC² + BC².
Solution :
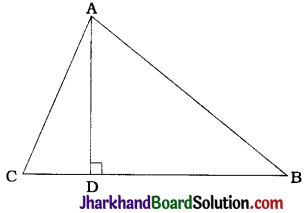
DB = 3CD
∴ BC = DB + CD = 3CD + CD
∴ BC = 4CD …………..(1)
In ΔADB, ∠D = 90°
∴ AB² = AD² + DB² (Pythagoras theorem) …………..(2)
In ΔADC, ∠D = 90°
∴ AC² = AD² + CD² (Pythagoras theorem) …………..(3)
Subtracting (3) from (2),
AB² – AC² = (AD² + DB²) – (AD² + CD²)
∴ AB² – AC² = DB² – CD²
∴ AB² – AC² = (DB + CD) (DB – CD)
∴ AB² – AC² = (BC) (3CD – CD)
∴ AB² – AC² = (BC) (2CD)
Multiplying the equation by 2, we get
2AB² – 2AC² = (BC) (4CD)
∴ 2AB² – 2AC² = (BC) (BC)
∴ 2AB² = 2AC² + BC² [By (1)]
Question 15.
In an equilateral triangle ABC, D is a point on side BC such that BD = \(\frac{1}{3}\)BC. Prove that 9AD² = 7AB².
Solution :
Given: In equilateral ΔABC, D is a point on BC such that BD = \(\frac{1}{3}\)BC.
To prove: 9AD² = 7AB²
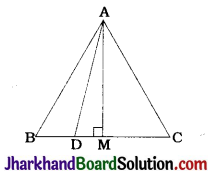
Construction: Draw AM ⊥ BC, such that M lies on BC.
Proof: ΔABC is an equilateral triangle. Suppose, AB = BC = AC = a
In equilateral ΔABC, AM is an altitude.
∴ AM is a median.
∴ BM = \(\frac{1}{2}\)BC = \(\frac{1}{2}\)a
∴ BD = \(\frac{1}{3}\)BC. Hence, DC = \(\frac{2}{3}\)BC
BD = \(\frac{1}{3}\)BC = \(\frac{1}{3}\)a
DM = BM – BD = \(\frac{1}{2}\)a – \(\frac{1}{3}\)a = \(\frac{1}{6}\)a
In ΔAMB, ∠M = 90°
∴ AB² = AM² + BM²
∴ a² = AM² + \(\frac{1}{4}\)a²
∴ AM² = \(\frac{3}{4}\)a²
In ΔAMD, ∠M = 90°
∴ AD² = AM² + DM²
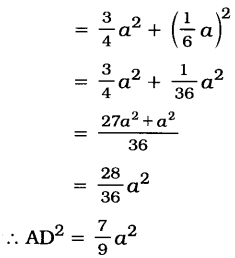
∴ 9AD² = 7a²
∴ 9AD2 = 7AB² (∵ AB = a)
![]()
Question 16.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution :
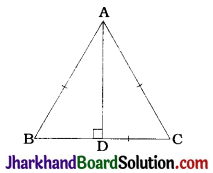
ABC is an equilateral triangle in which AD is an altitude.
Let AB = BC CA- a units.
In an equilateral triangle, an altitude is a median also.
∴ AD is a median.
∴ BD = \(\frac{1}{2}\)BC = \(\frac{a}{2}\)units
In ΔADB, ∠D = 90°
∴ AB² = AD² + BD²
∴ (a)² = AD² + (\(\frac{a}{2}\))²
∴ a² = AD² + \(\frac{a^2}{4}\)
∴ \(\frac{3}{4}\)a² = AD²
∴ 3a² = 4AD²
∴ 3 (side)² = 4 (altitude)²
Question 17.
Tick the correct answer and justify: In ΔABC, AB = 6\(\sqrt{3}\) cm, AC = 12 cm and BC= 6 cm. The angle B is:
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Solution :
In ΔABC, AB = 6\(\sqrt{3}\) cm = 10.38 cm (approx),
AC = 12 cm and BC = 6 cm
Here, AC is the longest side.
Then, 12² = 144 and
(6\(\sqrt{3}\))² + (6)² – 108 + 36 = 144
Thus, 12² = (6\(\sqrt{3}\))² + (6)²
Hence, by the converse of Pythagoras theorem, ΔABC is a right triangle in which the longest side AC is the hypotenuse and its opposite angle ∠B is a right angle.
Hence, the correct answer is (C) 90°.