JAC Class 10 Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन

Jharkhand Board JAC Class 10 Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन Important Questions and Answers.

JAC Board Class 10 Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन

अतिलयु उत्तरीय प्रश्न

प्रश्न 1.
गोलीय दर्पण की वक्रता-त्रिज्या तथा फोकस-दूरी में सम्बन्ध लिखिए।
उत्तर:
वक्रता त्रिज्या (R) = 2 x फोकस दूरी (f)।

प्रश्न 2.
अपने चेहरे का सीधा एवं बड़ा प्रतिबिम्ब देखने के लिए किस प्रकार के दर्पण का प्रयोग कीजिएगा?
उत्तर:
अवतल दर्पण का।

प्रश्न 3.
किस प्रकार के दर्पणों से केवल आभासी प्रतिबिम्ब बनते हैं?
उत्तर:
समतल दर्पणों तथा उत्तल दर्पणों से केवल आभासी प्रतिबिम्ब बनते हैं।

प्रश्न 4.
एक दर्पण, वस्तु के सापेक्ष सीधा व आकार में छोटा प्रतिबिम्ब बनाता है। यह किस प्रकार का दर्पण है? प्रतिबिम्ब वास्तविक है अथवा आभासी।
उत्तर:
उत्तल दर्पण (आभासी)।

प्रश्न 5.
किस प्रकार के दर्पण में रेखीय आवर्धन 1 से अधिक प्राप्त हो सकता है?
उत्तर:
अवतल दर्पण में।

प्रश्न 6.
प्रतिबिम्ब को पर्दे पर लेने के लिए किस प्रकार के दर्पण का प्रयोग कीजिएगा?
उत्तर:
अवतल दर्पण का।

प्रश्न 7.
समतल दर्पण की फोकस-दूरी कितनी होगी?
उत्तर:
अनन्त (∞) क्योंकि समान्तर आपतित किरणें परावर्तन के पश्चात् समान्तर ही रहती हैं-अर्थात् अनन्त पर ही मिलती हैं।

प्रश्न 8.
दर्पण का मुख्य अक्ष क्या होता है?
उत्तर:
दर्पण के ध्रुव एवं वक्रता-केन्द्र से गुजरने वाली रेखा को मुख्य अक्ष कहते हैं।

प्रश्न 9.
समान्तर किरणों को उदपसरित करने के लिए किस प्रकार का दर्पण उपयोगी होता है?
उत्तर:
उत्तल दर्पण।

प्रश्न 10. अवतल दर्पण के लिए u, v तथा f में सम्बन्ध लिखिए।
उत्तर:
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)

प्रश्न 11.
समतल दर्पण में तथा उत्तल दर्पण में बने प्रतिबिंबों में क्या समानताएँ होती हैं?
उत्तर:

• दोनों में प्रतिबिम्ब दर्पण के पीछे बनते हैं।
• दोनों में बने प्रतिबिम्ब आभासी तथा सीधे होते हैं।

प्रश्न 12.
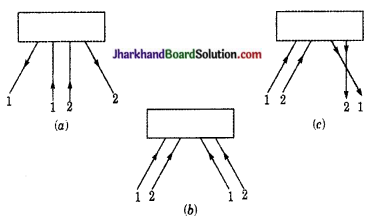
संलग्न चित्रों में आपतित एवं परावर्तित किरणों का मार्ग देखकर बताइए कि चित्र में प्रदर्शित बॉक्स में किस प्रकार का दर्पण स्थित हो सकता है?

उत्तर:

• उत्तल दर्पण (समान्तर आपतित किरणें परावर्तन के बाद अपसरित होती हैं)।
• समतल दर्पण (समान्तर आपतित किरणें समान्तर बनी रहती हैं)।
• अवतल दर्पण (समान्तर आपतित किरणें परावर्तन के बाद अपसरित होती हैं)।

प्रश्न 13.
परावर्तन किसे कहते हैं?
उत्तर:
जब प्रकाश किसी चिकने व चमकदार पृष्ठ पर पड़ता है तो इसका अधिकांश भाग विभिन्न दिशाओं में लौट आता है। इस घटना को प्रकाश का परावर्तन कहते हैं।

प्रश्न 14.
दर्पण कितने प्रकार के होते हैं?
उत्तर:
दर्पण मुख्यतः दो प्रकार के होते हैं-
(1) समतल दर्पण
(2) गोलीय दर्पण –

• अवतल दर्पण
• उत्तल दर्पण।

प्रश्न 15.
अवतल तथा उत्तल दर्पण में अन्तर समझाइए।
उत्तर:
अवतल दर्पण में बाह्य उभरे हुए गोलीय पृष्ठ पर पॉलिश कर दी जाती है जिससे प्रकाश का परावर्तन आन्तरिक पृष्ठ (अवतल) पर होता है। जबकि उत्तल दर्पण में भैंसे हुए गोलीय पृष्ठ पर पॉलिश कर दी जाती है जिससे प्रकाश का परावर्तन बाह्य पृष्ठ (उत्तल) पर होता है।

प्रश्न 16.
अवतल दर्पण के फोकस की परिभाषा लिखिए।
उत्तर:
अवतल दर्पण के मुख्य अक्ष के समान्तर आने वाली सभी प्रकाश किरणें दर्पण से परावर्तन के पश्चात् मुख्य अक्ष पर स्थित जिस बिन्दु पर एकत्रित होती हैं वह बिन्दु अवतल दर्पण का मुख्य फोकस कहलाता है।

प्रश्न 17.
लम्बन से क्या तात्पर्य है?
उत्तर:
लम्बन (विस्थापनाभास) – यदि दो वस्तुओं ( या प्रतिबिम्बों) को एक सीध में विभिन्न स्थितियों में रखकर देखें तो वे सम्पाती प्रतीत होती हैं। लेकिन आँख को दायें या बायें हटाने पर दोनों वस्तुएँ एक दूसरे से अलग होती हुई प्रतीत होती हैं। आँख से दूर वाली वस्तु (या प्रतिबिम्ब) पास वाली वस्तु की अपेक्षा उसी दिशा हटती दिखाई देती है जिस दिशा में आँख हटाते हैं। इस प्रकार आँख को इधर-उधर हटाने पर दो वस्तुओं के बीच सापेक्ष विस्थापन को लम्बन (या विस्थाना भास) कहते हैं।

प्रश्न 18.
गोलीय दर्पण के लिए 40 व में सम्बन्ध लिखिए।
अथवा
दर्पण सूत्र लिखिए एवं प्रत्येक संकेत का अर्थ लिखिए।
उत्तर:
गोलीय दर्पण के लिए u, v व f में निम्न सम्बन्ध को दर्पण सूत्र कहते हैं-
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
जहाँ
u = दर्पण से वस्तु की दूरी
v = दर्पण से प्रतिबिम्ब की दूरी
f = दर्पण की फोकस दूरी

प्रश्न 19.
गोलीय दर्पण कितने प्रकार के होते हैं? नाम लिखिए।
उत्तर:
गोलीय दर्पण दो प्रकार के होते हैं-

• अवतल दर्पण
• उत्तल दर्पण।

प्रश्न 20.
एक समतल दर्पण की फोकस दूरी तथा उसकी वक्रता त्रिज्या में सम्बन्ध लिखिए।
उत्तर:
एक समतल दर्पण की फोकस दूरी तथा उसकी वक्रता त्रिज्या दोनों ही अनन्त होती हैं।

प्रश्न 21.
एक अवतल दर्पण को यदि पानी में रख दिया जाये तो उसकी फोकस दूरी में क्या परिवर्तन होगा?
उत्तर:
कोई परिवर्तन नहीं होगा।

प्रश्न 22.
यदि एक वस्तु का प्रतिबिम्ब सदैव छोटा व आभासी बनता है तो दर्पण कैसा होगा?
उत्तर:
यदि वस्तु का प्रतिबिम्ब सदैव छोटा व आभासी बनता है तो दर्पण उत्तल होगा।

प्रश्न 23.
एक दर्पण में हम अपने चेहरे का सीधा व बड़ा प्रतिबिम्ब देख रहे हैं तो बताइए कि दर्पण कैसा होगा?
उत्तर:
अवतल दर्पण।

प्रश्न 24.
एक अवतल दर्पण के वक्रता केन्द्र पर एक वस्तु रखी है। इस वस्तु के प्रतिबिम्ब का रेखीय आवर्धन कितना होगा?
उत्तर:
जब वस्तु अवतल दर्पण के वक्रता केन्द्र पर होती है तो प्रतिबिम्ब का आकार वस्तु के आकार के बराबर, वास्तविक तथा उलटा होता है अतः प्रतिबिम्ब का रेखीय आवर्धन 1 होगा।

प्रश्न 25.
किसी अवतल दर्पण के ध्रुव तथा फोकस मध्य स्थित वस्तु के सापेक्ष उसके प्रतिबिम्ब की प्रकृति कैसी होगी?
उत्तर:
किसी अवतल दर्पण के ध्रुव तथा फोकस के मध्य स्थित वस्तु के सापेक्ष उसका प्रतिबिम्ब आभासी, सीधा व बड़ा होगा।

प्रश्न 26.
एक अवतल दर्पण में हम अपना वास्तविक तथा अपने आकार का प्रतिबिम्ब देख रहे हैं तो बताइए कि हमारी स्थिति क्या है?
उत्तर:
यदि हम अवतल दर्पण में अपना वास्तविक तथा अपने आकार का प्रतिबिम्ब देख रहे हैं तो हम अवतल दर्पण के वक्रता केन्द्र पर स्थित हैं।

प्रश्न 27.
अच्छी शेव के लिए कौन-सा दर्पण प्रयुक्त करना ठीक रहता है।
उत्तर:
अच्छी शेव करने के लिए अधिक फोकस दूरी का अवतल दर्पण ठीक रहता है।

प्रश्न 28.
दाढ़ी बनाने के लिए अवतल दर्पण का उपयोग क्यों किया जाता है?
उत्तर:
जब किसी वस्तु को अवतल दर्पण के सामने उसके ध्रुव एवं फोकस के बीच रखा जाता है तो उसका सीधा, आभासी एवं वस्तु से बड़ा प्रतिबिम्ब बनता है जो दाढ़ी बनाने के लिए उपयुक्त होता है।

प्रश्न 29.
उत्तल दर्पण के कोई दो उपयोग लिखिए।
उत्तर:
उत्तल दर्पण के दो उपयोग निम्नलिखित हैं-

• मोटर वाहनों में पीछे का ट्रैफिक देखने में।
• सड़क या चौराहे पर लगी बत्तियों में परावर्तक के रूप में।

प्रश्न 30.
अवतल दर्पण के दो उपयोग लिखिए।
उत्तर:
अवतल दर्पण के उपयोग निम्नलिखित हैं-

• टार्च, कार, मोटर, रेलवे इंजन के हैडलाइट में परावर्तक के रूप में।
• चिकित्सा में डॉक्टरों द्वारा कान, नाक, गला की जाँच करने में।

प्रश्न 31.
रैखिक आवर्धन से क्या तात्पर्य है? गोलीय दर्पण के लिए आवर्धन सूत्र लिखिए।
उत्तर:
रैखिक आवर्धन- यदि वस्तु एवं प्रतिबिम्ब की लम्बाई मुख्य अक्ष के लम्बवत् नापी जाये तो प्रतिबिम्ब की लम्बाई एवं वस्तु की लम्बाई के अनुपात को रेखीय आवर्धन कहते हैं।

प्रश्न 32.
प्रकाश क्या है? इसके प्राकृतिक स्रोत का नाम लिखिए।
उत्तर:
प्रकाश ऊर्जा का वह रूप है जिसकी सहायता से नेत्र द्वारा देखने की अनुभूति होती है। प्रकाश का प्राकृतिक स्रोत सूर्य है।

प्रश्न 33.
किसी अवतल दर्पण की फोकस दूरी = 20 सेमी है, उसकी वक्रता त्रिज्या ज्ञात कीजिए।
उत्तर:
दिया है अवतल दर्पण की-
फोकस दूरी (f) = – 20 सेमी
वक्रता त्रिज्या (R) = ?
∵ R = 2 x f
∴ R = 2 x (- 20) = – 40 सेमी
अतः अवतल दर्पण की वक्रता त्रिज्या 40 सेमी होगी।

प्रश्न 34.
यदि कोई अवतल दर्पण एक ऐसे खोखले गोले का भाग है जिसकी त्रिज्या 40 सेमी है, तो अवतल दर्पण की फोकस दूरी क्या होगी?
उत्तर:
दिया है अवतल दर्पण की-
वक्रता त्रिज्या (R) = 40 सेमी.
फोकस दूरी (f) =?
∵ R = 2 x f
⇒ f = \(\frac{R}{2}=\frac{-40}{2}\) = – 20 सेमी
अतः अवतल दर्पण की फोकस दूरी 20 सेमी है।

प्रश्न 35.
प्रकाश की एक किरण वायु से आती हुई स्वच्छ जल के स्थिर तल पर आपतित होती है। यह किरण के तल पर परावर्तित होगी या अपवर्तित या दोनों।
उत्तर:
जल के तल से प्रकाश का कुछ अंश परावर्तित तथा अधिकांश अपवर्तित होगा।

प्रश्न 36.
एक माध्यम (1) में किसी प्रकाश किरण का आपतन कोण 35° तथा दूसरे माध्यम (2) में उसी किरण का अपवर्तन कोण 45° है। दोनों में से किस माध्यम का निरपेक्ष अपवर्तनांक अधिक है?
उत्तर:
माध्यम (1) का।

प्रश्न 37.
किसी माध्यम का निरपेक्ष अपवर्तनांक, वायु के सापेक्ष उस माध्यम के अपवर्तनांक के लगभग बराबर माना जाता है। वायु का निरपेक्ष अपवर्तनांक लगभग कितना होगा?
उत्तर:
वायु का निरपेक्ष अपवर्तनांक लगभग 1 होगा।

प्रश्न 38.
दो माध्यमों A तथा B के अपवर्तनांक n_A तथा n_B हैं। इनमें से किस माध्यम से किस माध्यम में जाने पर प्रकाश का पूर्ण-आंतरिक परावर्तन संभव है यदि N_A > n_B?
उत्तर:
माध्यम A से माध्यम B की ओर।

प्रश्न 39.
प्रकाश के ‘स्पेक्ट्रम’ से क्या तात्पर्य है?
उत्तर:
किसी मिश्रित प्रकाश के संयोजी वर्णों (रंगों) को उनके तरंगदैघ्यों के आरोही अथवा अवरोही क्रम को प्रकाश का स्पेक्ट्रम कहते हैं।

प्रश्न 40.
सौर प्रकाश के स्पेक्ट्रम के रंगों को अपवर्तनांक बढ़ते हुए क्रम में लिखिए।
उत्तर:
लाल (Red), नारंगी (Orange), पीला (Yel-low), हरा (Green), आसमानी (Blue), नीला (Indigo), बैंगनी (Violet)।

प्रश्न 41.
किसी प्रिज्म के न्यूनतम विचलन कोण, प्रिज्म कोण एवं प्रिज्म के पदार्थ के अपवर्तनों में सम्बन्ध लिखिए।
उत्तर:
यदि प्रिज्म कोण A, न्यूनतम विचलन कोण δm तथा अपवर्तनांक n हो तो
n = \(\frac{\sin [(A+\delta m) / 2]}{\sin [A / 2]}\)

प्रश्न 42.
श्वेत प्रकाश के किन रंगों के लिए काँच का अपवर्तनांक अधिकतम और न्यूनतम होता है?
उत्तर:
बैंगनी रंग श्वेत प्रकाश के लिए काँच अपवर्तनांक अधिकतम और लाल के लिए न्यूनतम होता है।

प्रश्न 43.
पूर्ण परावर्तक प्रिज्म क्या है?
उत्तर:
एक ऐसा काँच का प्रिज्म जो समकोण समद्विबाहु त्रिभुजाकार होता है, वह पूर्ण परावर्तक प्रिज्म होता है जो पूर्ण आन्तरिक परावर्तन के सिद्धान्त पर कार्य करता है।

प्रश्न 44.
पूर्ण परावर्तन प्रिज्म के दो उपयोग लिखो।
उत्तर:
पूर्ण परावर्तक प्रिज्म का उपयोग प्रकाशिक यन्त्रों में होता है-

• 90° के विचलन के लिए पेरिस्कोप में।
• 180° के विचलन के लिए बायनोकुलर में।

प्रश्न 45.
प्रकाशिक तन्तु क्या है?
उत्तर:
प्रकाशिक तन्तु पूर्ण आंतरिक परावर्तन के सिद्धान्त पर आधारित ऐसी युक्ति है जिसके द्वारा प्रकाशिक संकेत को इसकी तीव्रता में बिना क्षय हुए एक स्थान से दूसरे स्थान तक वक्रीय पथ से स्थानांतरित किया जा सकता है।

प्रश्न 46.
लेंस किसे कहते हैं?
उत्तर:
दो गोलीय तलों में घिरे पारदर्शीय माध्यम को लेंस कहते हैं जिसका एक तल गोलीय व दूसरा तल उत्तल, अवतल अथवा समतल होता है।

प्रश्न 47.
लेंस के प्रकारों के नाम लिखो।
उत्तर:
लेंस मुख्यतः दो प्रकार के होते हैं-

• उत्तल लेंस (अभिसारी लेंस)
• अवतल लेंस (अपसारी लेंस)

प्रश्न 48.
अभिसारी और अपसारी लेंस की विशेषता क्या है?
उत्तर:

• अभिसारी लेंस की विशेषता जब प्रकाश की समान्तर किरण पुंज अभिसारी लेंसों में से होकर गुजरती है तो लेंस से अपवर्तन के पश्चात् उन्हें एक बिन्दु पर केन्द्रित कर देता है।
• अपसारी लेंस की विशेषता – जब प्रकाश की समान्तर किरण पुंज अपसारी लेंसों में से होकर गुजरती है तो लेंस से अपवर्तन के पश्चात् उन्हें एक बिन्दु से अपसरित करता हुआ प्रतीत होती है।

प्रश्न 49.
उत्तल लेंस के उपयोग लिखो।
उत्तर:
उत्तल लेंस के निम्नलिखित उपयोग हैं-

• प्रकाशिक यन्त्रों, जैसे दूरदर्शी, कैमरा आदि।
• दूर दृष्टि दोष दूर करने हेतु चश्में में।

लघु उत्तरीय प्रश्न

प्रश्न 1.
आवश्यक किरण आरेख बनाकर निम्नलिखित की परिभाषा दीजिए-
(i) वक्रता केन्द्र तथा वक्रता त्रिज्या,
(ii) अवतल दर्पण का मुख्य फोकस तथा फोकस दूरी
(iii) उत्तल दर्पण का मुख्य फोकस फोकस दूरी।
उत्तर:
(i) वक्रता केन्द्र तथा वक्रता त्रिज्या वक्रता केन्द्र (Centre of Curvature) – गोलीय दर्पण जिस खोखले गोले का भाग होता है, उसके केन्द्र को वक्रता केन्द्र कहा जाता है। चित्र में इसे C अक्षर से प्रदर्शित किया गया है।

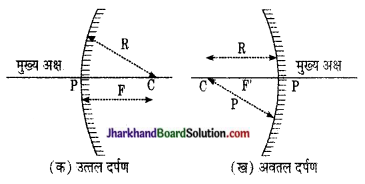
वक्रता त्रिज्या (Radius of Curvature)- गोलीय दर्पण का भाग होता है, उसकी त्रिज्या को गोलीय दर्पण की वक्रता त्रिज्या कहते हैं अतः दर्पण के किसी भी बिन्दु को वक्रता केन्द्र से मिलाने वाली रेखा की लम्बाई को वक्रता त्रिज्या कहते हैं। सामान्यतः यह दूरी वक्रता केन्द्र (C) से ध्रुव (P) तक नापी जाती है अत: राशि (L/R) को दर्पण की वक्रता कहते हैं।

(ii) अवतल दर्पण का मुख्य फोकस तथा फोकस – दूरी (Focal Length and Principal Focus of Concave Mirror) – अवतल मुख्य अक्ष के समान्तर आपतित किरणें परावर्तन के पश्चात् दर्पण के मुख्य अक्ष पर स्थित जिस बिन्दु से होकर जाती हैं- उसे मुख्य फोकस कहते हैं। दर्पण के ध्रुव से मुख्य फोकस की दूरी को फोकस दूरी कहते हैं।

(iii) उत्तल दर्पण का मुख्य फोकल तथा फोकस दूरी (Focal Length and Principal Focus Convex Mirror) – उत्तल दर्पण के मुख्य अक्ष के समान्तर आपतित किरणें परावर्तन के पश्चात् मुख्य अक्ष के जिस बिन्दु अपसरित होती प्रतीत होती हैं। उसे मुख्य फोकस कहते हैं।

प्रश्न 2.
‘प्रतिबिम्ब’ से क्या तात्पर्य है? आभासी तथा वास्तविक प्रतिबिम्ब में क्या अन्तर होता है?
उत्तर:
प्रतिबिम्ब (Image) – दर्पण के तल से परावर्तन के पश्चात् प्रकाश किरणें, जिस बिन्दु पर अभिसरित (converge) होती हैं अथवा जिस बिन्दु से अपसरित (diverge) होती प्रतीत होती हैं, उसे वस्तु का प्रतिबिम्ब कहते हैं [चित्र (क) तथा (ख)]

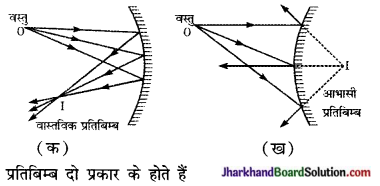
(i) वास्तविक प्रतिबिम्ब (Real Image) – यदि परावर्तन के पश्चात् किरणें वास्तव में किसी बिन्दु पर अभिसरित होती हैं, , तो इसे वास्तविक प्रतिबिम्ब कहते हैं। चित्र (क) में 1, वस्तु O का वास्तविक प्रतिबिम्ब है। यदि स्थान I पर कोई पर्दा (Screen) रखा जाय तो यह प्रतिबिम्ब एक प्रकाश बिन्दु के रूप में दिखाई देगा। अतः वास्तविक प्रतिबिम्ब को पर्दे पर लिया जा सकता है।

(ii) आभासी प्रतिबिम्ब (Virtual Image)- यदि परावर्तन के पश्चात् किरणें अपसारी (divergent ) हों तो वे किसी बिन्दु पर वास्तव में अभिसरित नहीं होतीं। ऐसी किरणें दर्पण के पीछे स्थित किसी बिन्दु से अपसरित (di- verge) होती प्रतीत होती हैं। परावर्तन के पश्चात् प्रकाश की अपसारी किरणें, जिस बिन्दु से अपसरित होती प्रतीत होती हैं, उसे वस्तु का आभासी

प्रतिबिम्ब कहते हैं। चित्र (ख) में I, वस्तु O का आभासी प्रतिबिम्ब है। आभासी प्रतिबिम्ब को पर्दे पर नहीं देखा जा सकता क्योंकि इस बिन्दु’ प्रकाश वास्तव में नहीं पहुँचता।

प्रश्न 3.
केवल किरण आरेख बनाकर, अवतल दर्पण में प्रतिबिम्ब का बनना प्रदर्शित कीजिए जब
(i) वस्तु मुख्य फोकस पर हो
(ii) प्रतिबिम्ब मुख्य फोकस पर बने।
उत्तर:
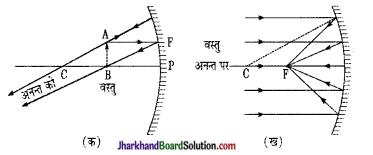
(i) वस्तु मुख्य फोकस (F) पर

(ii) प्रतिबिम्ब मुख्य फोकस (F) पर

प्रश्न 4.
अवतल दर्पण आभासी प्रतिबिम्ब बनने का किरण आरेख बनाइए। इसके लिए वस्तु की स्थिति का उल्लेख कीजिए।
उत्तर:
वस्तु की स्थिति दर्पण के मुख्य फोकस (F) तथा ध्रुव (P) के बीच कहीं पर।

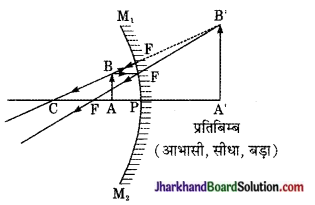
प्रश्न 5.
उत्तल दर्पण किस प्रकार का प्रतिबिम्ब बनता है? किरण आरेख बनाकर बताइए।
उत्तर:
प्रतिबिम्ब दर्पण के पीछे, आभासी सीधा तथा वस्तु के आकार से छोटा बनता है। प्रतिबिम्ब की स्थिति ध्रुव तथा मुख्य फोकस के बीच में ही होती है।

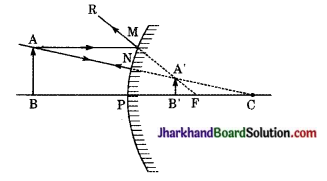
प्रश्न 6.
आरेख बनाकर स्पष्ट कीजिए कि उत्तल दर्पण की फोकस – दूरी धनात्मक तथा अवतल दर्पण की फोकस – दूरी ऋणात्मक क्यों मानी जाती है?
उत्तर:
दर्पणों में दूरियों के चिन्ह निर्देशांक ज्यामिति की प्रणाली के अनुसार निर्धारित किये जाते हैं। निर्देशांक ज्यामिति की चिन्ह प्रणाली के अनुसार, दर्पण के ध्रुव को मूल बिन्दु, मुख्य अक्ष को X- अक्ष तथा मुख्य अक्ष के लम्बवत् ध्रुव से गुजरने वाली रेखा को Y- अक्ष मानते हैं। इस प्रणाली के अनुसार-
(1) गोलीय दर्पणों (और लेंसों) पर प्रकाश किरणें सदैव बायीं ओर से डाली जाती हैं।

(2) समस्त दूरियाँ दर्पण के ध्रुव से मुख्य अक्ष के अनुदिश नापी जाती हैं।

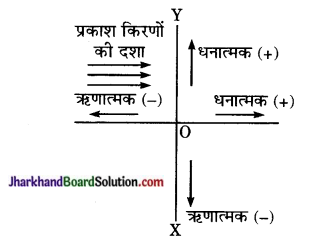
(3) दर्पण के ध्रुव से दायीं नापी गयी दूरियाँ धनात्मक चिन्ह (+) के साथ ली जाती हैं या दूरियाँ जो आपतित किरण जाती हैं।

(4) दर्पण के ध्रुव से बायीं ओर नापी गयी दूरियाँ ऋणात्मक चिन्ह (-) के साथ ली जाती हैं या वे दूरियाँ जो आपतित किरण की विपरीत दिशा में नापी जाती हैं, ऋणात्मक चिन्ह (-) के साथ ली जाती हैं।

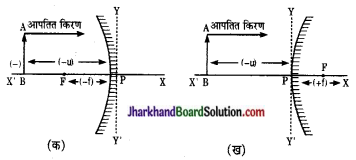
चित्र (क) तथा (ख) में अवतल दर्पण तथा उसल दर्पण के मुख्य फोक्सों की स्थितियाँ प्रदर्शित हैं। चित्रास स्पष्ट है कि उत्तल दर्पण में फोकस दूरी () धनात्मको तथा अवतल दर्पण में ऋणात्मक (-) होगी।

प्रश्न 7.
केवल प्रतिबिम्ब देखकर कैसे विभेद कीजिएगा?
(i) उत्तल दर्पण एवं अवतल दर्पण में,
(ii) उत्तल दर्पण एवं समतल दर्पण में,
(iii) समतल दर्पण एवं अवतल दर्पण में।
उत्तर:
(i) किसी दूरस्थ वस्तु का प्रतिबिम्ब उत्तल दर्पण में सीधा परन्तु अवतल दर्पण में उल्टा दिखाई देगा। किसी निकटस्थ वस्तु का प्रतिबिम्ब उत्तल दर्पण में छोटा परन्तु अवतल दर्पण में बड़ा दिखाई देगा।

(ii) उत्तल दर्पण में किसी भी वस्तु का प्रतिबिम्ब छोटा परन्तु समतल दर्पण में वस्तु के समान आकार का दिखाई देगा।

(iii) समतल दर्पण में दूरस्थ वस्तु का प्रतिबिम्ब सीधा परन्तु अवतल दर्पण में उल्टा दिखाई देगा। समतल दर्पण में निकटस्थ वस्तु का प्रतिबिम्ब समान आकार का परन्तु अवतल दर्पण में बड़ा दिखाई देगा।

प्रश्न 8.
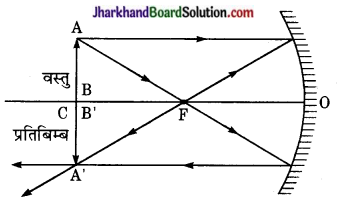
अवतल दर्पण में वस्तु को किस स्थिति पर रखने से रेखीय आवर्धन 1 होता है? आवश्यक आरेख बनाकर बताइए।
उत्तर:
वस्तु को दर्पण के वक्रता केन्द्र पर रखने से प्रतिबिम्ब का आकार वस्तु के आकार के समान होता है अतः आवर्धन 1 होता है।

प्रश्न 9.
समान्तर आपाती किरणों के परावर्तन के आरेख बनाकर स्पष्ट कीजिए कि किस प्रकाश का दर्पण अभिसारी (convergent) होता है तथा किस प्रकार का दर्पण अपसारी (divergent )?
उत्तर:
चित्र (क) तथा (ख) में अवतल तथा उत्तल दर्पण से समान्तर आपाती किरणों का परावर्तन दिखाया गया है।

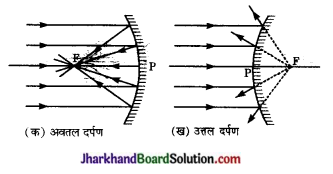
चित्र (क) से स्पष्ट है कि अवतल दर्पण समान्तर’ किरणों को एक बिन्दु (मुख्य फोकस) पर केन्द्रित अथवा अभिसरित कर देता है। अतः अवतल दर्पण अभिसारी होता है।

इसके विपरीत उत्तल दर्पण पर आपतित समान्तर किरणें परावर्तन के पश्चात् एक बिन्दु (फोकस) से अपसरित होती प्रतीत होती हैं। अतः उत्तल दर्पण अपसारी होता है।

प्रश्न 10.
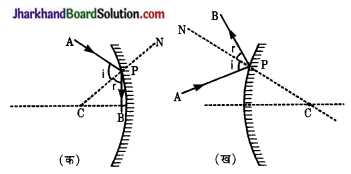
किरण आरेख बनाकर, प्रदर्शित कीजिए कि-
(i) अवतल दर्पण
(ii) उत्तल दर्पण में परावर्तन के नियम का पालन किस प्रकार होता है?
उत्तर:
दोनों चित्रों में आपतित किरण AP दर्पण से परावर्तन के पश्चात् किरण PB के रूप में प्रदर्शित है। परावर्तन के बिन्दु P को दर्पण की वक्रता केन्द्र C से मिलाने पर अभिलम्ब CN प्राप्त होता है। दोनों ही दर्पणों में परावर्तन के नियम के अनुसार आपतन कोण (i) परावर्तन कोण (r) के बराबर होता है।

प्रश्न 11.
किरण- आरेख बनाकर समझाइए कि अवतल दर्पण द्वारा, किसी बिन्दु प्रकाश स्रोत से-
(i) समान्तर किरण पुंज,
(ii) अभिसारी किरण- पुंज।
(iii) अपसारी किरण पुंज कैसे प्राप्त किया जा सकता है?
उत्तर:
अवतल दर्पण –
(i) अवतल दर्पण के ध्रुव और फोकस के बीच रखी वस्तु का प्रतिबिम्ब वस्तु के सापेक्ष सीधा तथा बड़ा बनता है। अतः अवतल दर्पण का उपयोग दाढ़ी बनाने में किया जाता है।

(ii) कान, नाक व गले के आन्तरिक भागों की जाँच करने के लिए डॉक्टर अवतल दर्पण का उपयोग करते हैं।

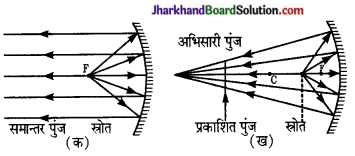
(iii) अवतल दर्पण का उपयोग ऐसे परावर्तक के रूप में किया जाता है जो किसी प्रकाश स्रोत के प्रकाश को समान्तर पुंज (Parallel beam) के रूप में परिवर्तित करें. अथवा किसी अभिसारी किरण पुंज के रूप में किसी वस्तु पर केन्द्रित करें।

पहली दशा में प्रकाश स्रोत को दर्पण के मुख्य फोकस (F) पर रखना होगा [चित्र (क)]

दूसरी दशा में प्रकाश – स्रोत को दर्पण के मुख्य फोकस (F) तथा वक्रता केन्द्र (C) के बीच में इस प्रकार रखना होगा कि दर्पण से परावर्तित संपूर्ण प्रकाश, वस्तु पर केन्द्रित हो।

इस प्रकार का उपयोग बहुधा सूक्ष्मदर्शी, प्रोजेक्टर आदि में किया जाता है-

(iv) अवतल दर्पण का उपयोग परावर्तक दूरदर्शी (Re-flecting telescope) में किया जाता है।

प्रश्न 12.
रेखीय आवर्धन की परिभाषा लिखिए।
उत्तर:
रेखीय आवर्धन वस्तु के प्रतिबिम्ब की लम्बाई एवं वस्तु की लम्बाई के अनुपात को प्रतिबिम्ब का रेखीय आवर्धन कहते हैं। यदि प्रतिबिम्ब की लम्बाई तथा वस्तु की लम्बाई हो तो प्रतिबिम्ब का रेखीय आवर्धन M = \(\frac { I }{ O }\)।

प्रश्न 13.
अवतल दर्पण के ध्रुव एवं फोकस के मध्य रखी वस्तु के प्रतिबिम्ब बनने का किरण आरेख खींचिए।
उत्तर:
जब वस्तु अवतल दर्पण के सामने ध्रुव तथा फोकस के मध्य रखी हो तो प्रतिबिम्ब दर्पण के पीछे, आभासी, सीधा व वस्तु से बड़ा बनता है।

प्रश्न 14.
किसी लेंस के लिए फोकस दूरी एवं प्रकाशित केन्द्र को परिभाषित करो।
उत्तर:
(i) लेंस की फोकस दूरी-लेंस के प्रकाशिक केन्द्र से मुख्य फोकस की दूरी को लेंस की फोकस दूरी कहते हैं। इसे संकेत से दर्शाते हैं।

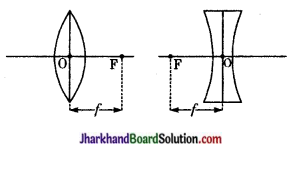
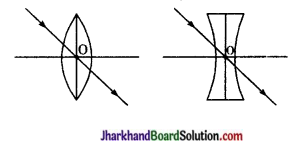
(ii) प्रकाशिक केन्द्र-लेंस के मुख्य अक्ष पर स्थित वह बिन्दु जिससे गुजरने वाली प्रकाश किरण अपवर्तन के पश्चात् आपतित किरण की दिशा में निर्गमित होती है, लेंस का प्रकाशिक केन्द्र कहलाता है।

प्रश्न 15.
क्या कारण है कि रात को तारे टिमटिमाते दिखाई देते हैं जबकि चन्द्रमा नहीं।
उत्तर:
तारों का टिमटिमाना प्रकाश के अपवर्तन के कारण होता है। तारों से आने वाला प्रकाश वायु की विभिन्न घनत्व की परतों से अपवर्तित होता है। वायुमण्डल की परिस्थिति (ताप) जल्दी-जल्दी बदलने के कारण वायुमण्डल की परतों का घनत्व तथा अपवर्तनांक भी बदलता रहता है जिससे तारों की आभासी स्थिति एक सी नहीं रहती है बल्कि प्रत्येक क्षण बदलती है। इसलिए तारे टिमटिमाते प्रतीत होते हैं।

चन्द्रमा पृथ्वी से तारों की अपेक्षा पास होने के कारण आकार में बड़ा दिखाई देता है तथा तारे की अपेक्षा कहीं अधिक किरणें भेजता है। अतः किरणों की संख्या अधिक होने के कारण किरणों पर होने वाले परिवर्तन का आँख पर कोई विशेष प्रभाव नहीं पड़ता है, इसलिए चन्द्रमा टिमटिमाता प्रतीत नहीं होता है।

प्रश्न 16.
तालाब में पड़ी मछली वहाँ नहीं होती है जहाँ वह दिखायी देती है। कारण बताइये।
उत्तर:
जब हम स्वच्छ जल से भरे किसी तालाब की तली को ऊर्ध्वाधर लम्बवत् देखते हैं तो हमें तली का प्रत्येक बिन्दु ऊपर उठा दिखाई देता है अर्थात् तालाब की आभासी गहराई, उसकी वास्तविक गहराई से कम प्रतीत होती है। चूँकि वायु के सापेक्ष जल का अपवर्तनांक

अर्थात् जल के भीतर स्थित किसी वस्तु को बाहर से देखने पर वह अपनी वास्तविक गहराई की \(\frac { 3 }{ 4 }\) गहराई पर ही दिखाई देगी। यही कारण है कि तालाब में पड़ी मछली वहाँ नहीं होती है जहाँ वह दिखाई देती है।

प्रश्न 17.
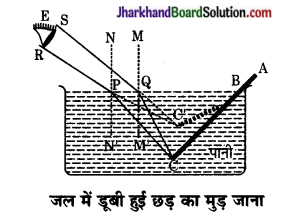
जल में डूबी हुई सीधी छड़ मुड़ी हुई दिखाई देती है? कारण स्पष्ट कीजिए।
उत्तर:
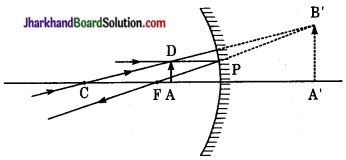
चित्रानुसार छड़ के बिन्दु C से चलने वाली प्रकाश की किरणें CP और CQ अपवर्तन के पश्चात् PR और QS मार्ग पर चलती हैं तथा नेत्र E को बिन्दु C से आती हुई प्रतीत होती हैं अर्थात् बिन्दु C का आभासी प्रतिबिम्ब है। इसी प्रकार BC के प्रत्येक बिन्दु के आभासी प्रतिबिम्ब BC के संगत बिन्दुओं पर बनते हैं अतः जल में डूबा हुआ भाग BC, BC’ पर प्रतीत होता है। इस प्रकार जल की सतह से सीधी छड़ मुड़ी प्रतीत होती है।

प्रश्न 18.
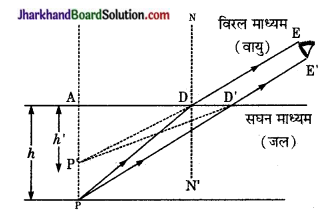
पानी में पड़ा सिक्का सतह दिखाई देता है? कारण दीजिए।
उत्तर:
चित्रानुसार पानी में पड़ा सिक्का P से आने वाली प्रकाश किरणें सघन माध्यम (जल) से विरल माध्यम (वायु) में आती हैं अतः अभिलम्ब से दूर हट जाती हैं जो P’ से आती हुई प्रतीत होती हैं जिससे सिक्के P का आभासी प्रतिबिम्ब P’ बनता है और सिक्का उठा हुआ P’ पर दिखाई देता है।

प्रश्न 19.
स्वच्छ जल के तालाब की गहराई, उसकी वास्तविक गहराई से कम क्यों प्रतीत होती है?
उत्तर:
माना तालाब के जल की सतह PR है। इसकी तली में स्थित वस्तुएँ O₁, O₂, O₃, इत्यादि से चलने वाली प्रकाश किरणें OP₁, OP₂, OP₃ …….. जल (सघन माध्यम) से चलकर वायु के अपवर्तक के पश्चात् E स्थान से देखी जाती हैं। नेत्र E को ये क्रमश: I₁, I₂, I₃……. बिन्दुओं से आती हुई प्रतीत होती हैं अतः स्पष्ट है कि दर्शक को दूर स्थित वस्तुएँ समीप स्थित वस्तुओं की अपेक्षा अधिक उठी हुई प्रतीत होती हैं। यही कारण है तालाब कम गहरा दिखाई देता है।

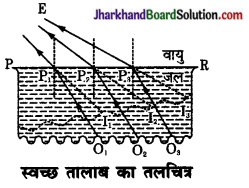
प्रश्न 20.
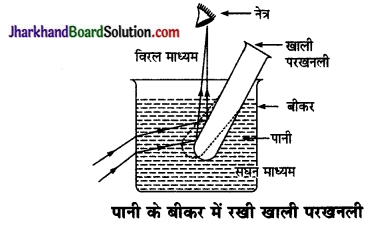
पानी को बीकर में रखी खाली परख नली चाँदी जैसी चमकदार दिखायी देती है। कारण समझाइए।
उत्तर:
पानी के बीकर में रखी खाली परखनली चाँदी जैसी चमकदार दिखायी देती है, इसका कारण यह है कि प्रकाश किरणें जल (सघन माध्यम) से परखनली की वायु (विरल माध्यम) में प्रवेश करती हैं। अतः वे किरणें जो जल के क्रान्तिक कोण (49° लगभग) से बड़ा कोण बनाते हुए परखनली पर आपतित होती हैं पूर्ण परावर्तित हो जाती हैं।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
अवतल दर्पण का उदाहरण लेकर सिद्ध कीजिए कि गोलीय दर्पण की फोकस दूरी, दर्पण की वक्रता त्रिज्या की आधी होती है।
उत्तर:
चित्र में एक किरण AM अवतल दर्पण के मुख्य अक्ष (CP) के समान्तर आपतित होती है। यह किरण दर्पण से MF दिशा में परावर्तित है जहाँ F दर्पण का फोकस है। दर्पण का ध्रुव P तथा वक्रता केन्द्र C है बिन्दु M पर अभिलम्ब MC है क्योंकि दर्पण के किसी बिन्दु से वक्रता केन्द्र को मिलाने वाली रेखा दर्पण पर अभिलम्ब होती है। ∠AMC आपतन कोण तथा ∠FMC परावर्तन कोण है।

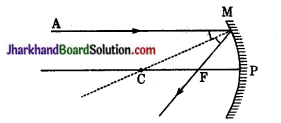
परावर्तन के नियमानुसार,
∠AMC = ∠FMC
∵ AM || CP तथा CM इन्हें काटती है। … (1)
∴ ∠AMC = ∠FCM (एकान्तर कोण) … (2)
समीकरण (1) और समीकरण (2) से,
∠FMC = ∠FCM
अतः इन कोणों सम्मुख ∆FMC की भुजाएँ भी बराबर होंगी,
अर्थात् FC = MF … (3)
यदि अवतल दर्पण द्वारक बहुत अधिक छोटा है, तो बिन्दु M ध्रुव P के बहुत निकट होगा और तब इस दशा में,
FM = FP (लगभग) … (4)
समीकरण (3) में FM = FP रखने पर,
FC = FP
अर्थात् F, CP का मध्य बिन्दु होगा। …(5)
समीकरण (5) के दोनों पक्षों में FP जोड़ने पर,
FC + FP = FP + FP
या, PC = 2.FP
या, FP = \(\frac { PC }{ 2 }\)
अर्थात् फोकस दूरी = \(\frac { 1 }{ 2 }\) x वक्रता त्रिज्या
अथवा f = \(\frac { R }{ 2 }\)

प्रश्न 2.
उत्तल दर्पण के लिए सूत्र f = \(\frac { R { 2 \) प्राप्त कीजिए, जबकि तथा R अपने सामान्य अर्थों में प्रयुक्त हैं।
उत्तर:
उत्तल दर्पण के लिए फोकस दूरी एवं वक्रता त्रिज्या में सम्बन्ध (Relation between Radius of Curvature and Focal Length by Con- vex Mirror) – माना M₁ M₂ एक उत्तल दर्पण है, जिसके फोकस F. वक्रता केन्द्र C तथा ध्रुव P हैं। अतः इसकी वक्रता त्रिज्या PC = R तथा फोकस दूरी PF = f है। माना, एक प्रकाश किरण AB मुख्य अक्ष PC के समान्तर दर्पण पर आपतित होती है। परन्तु बिन्दु B पर CN अभिलम्ब है। अतः यह किरण BD दिशा में परावर्तित हो जाती है तथा फोकस F से आती हुई प्रतीत होती है। ∠ABN आपतन कोण तथा ∠DBN परावर्तन कोण है।
अत: ∠ABN = ∠DBN  (परावर्तन के नियम से)
तथा ∠ABN = ∠FBC (शीर्षाभिमुख कोण) … (1)
अब AB एवं PC परस्पर समान्तर हैं तथा NC इन्हें काटती है,
∴ ∠ABN = ∠FCB (संगत कोण) … (2)
समीकरण (1) व समीकरण (2) से ∠FBC = ∠FCB
अब ∆FBC में, ∠FBC = ∠FCB
FC = FB … (3)

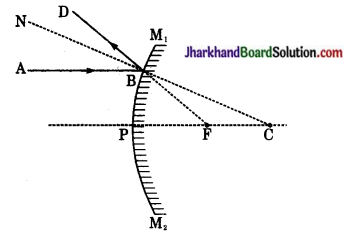
यदि उत्तल दर्पण बहुत अधिक छोटे द्वारक का है, तो बिन्दु B ध्रुव P के बहुत निकट होगा और तब इस दशा में
PB = FP (लगभग) … (4)
समीकरण (3) में FB = FP रखने से,
FC = FP … (5)
समीकरण (5) के दोनों ओर PF जोड़ने पर,
PF + FC = PF + PF
PC = 2 PF
∴ PF = \(\frac { 1 }{ 2 }\) PC
अर्थात् फोकस-दूरी = \(\frac { 1 }{ 2 }\) x वक्रता त्रिज्या

प्रश्न 3.
अवतल दर्पण के समुख स्थित वस्तु के प्रतिबिम्ब का बनना किरण आरेख द्वारा प्रदर्शित कीजिए, जबकि वस्तु की स्थिति-
(i) वक्रता केन्द्र से अधिक दूरी पर हो,
(ii) वकता केन्द्र पर हो,
(iii) वक्रता केन्द्र तथा फोकस कें षीच हो,
(iv) फोकस तथा दर्पण के बीच में हो।
प्रत्येक प्रतिबिम्ब की प्रकृति बताइए।
उत्तर:
(i) वस्तु दर्पण के वक्रता केन्द्र से अधिक दूरी पर हो (u > R)
प्रतिबिम्ब की स्थिति-मुख्य फोकस तथा वक्रता केन्द्र के बीच में [R > v > F]
आकार-वस्तु से छोटा I = \(\frac { v { u \) x O [ [I] < O]
प्रकृति- वास्तविक तथा उल्टा।

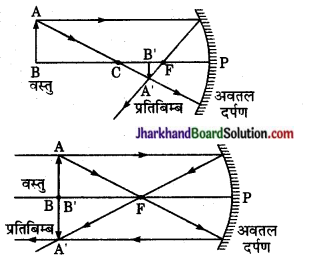
(ii) वस्तु दर्पण के वक्रता केन्द्र पर हो – [u = R]
प्रतिबिम्ब की स्थिति वक्रता केन्द्र पर [v = R]
आकार-वस्तु के समान [I = O]
प्रकृति-वास्तविक तथा उल्टा।

(iii) वस्तु दर्पण के वक्रता केन्द्र तथा मुख्य फोकस के बीच में [R > u > f]
प्रतिविम्ब की स्थिति वक्रता केन्द्र के आगे (v > R)
आकार वस्तु से बड़ा (I > O)
प्रकृति – वास्तविक तथा उल्टा।

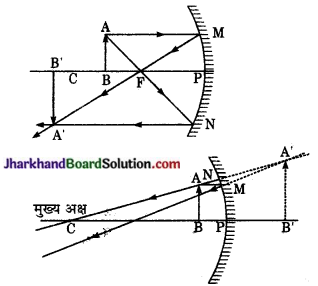
(iv) वस्तु फोकस तथा दर्पण के बीच हो [u < f]
प्रतिबिम्ब की स्थिति दर्पण के पीछे।
आकार – वस्तु से बड़ा (I > O)
प्रकृति – सीधा तथा आभासी।

प्रश्न 4.
अवतल दर्पण (गोलीय दर्पण) के लिए सूत्र \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\) का निगमन कीजिए।
उत्तर:
माना M₁M₂ एक अवतल दर्पण है जिसका P ध्रुव तथा C वक्रता केन्द्र है। दर्पण की मुख्य अक्ष पर AB एक वस्तु रखी है जिनका प्रतिबिम्ब A’B’ बनता है। दर्पण के ध्रुव (P) से वस्तु की दूरी PA माना है। ध्रुव से प्रतिबिम्ब की दूरी PA’ माना है तथा दर्पण की फोकस दूरी PF माना है। मुख्य अक्ष के समान्तर प्रकाश किरण है। D से मुख्य अक्ष पर लम्ब DN है।
अतः DN = AB
अब ∆ABC तथा ∆A’B’C में।
∠BAC = ∠B’A’C (प्रत्येक समकोण है)
∠BCA = ∠B’C’A ( शीर्षाभिमुख कोण)
अतः तीसरा कोण ABC = CB’A’
अर्थात् दोनों त्रिभुज समरूप हैं।
∴ \(\frac{A B}{A^{\prime} B^{\prime}}=\frac{C A}{C A^{\prime}}\) …(i)
अब ∆DNF तथा ∆ABF भी समरूप हैं
∴ \(\frac{D N}{A^{\prime} B^{\prime}}=\frac{F N}{F A^{\prime}}\) …(2)
समीकरण ( 1 ) व समीकरण (2) से,
∴ \(\frac{C A}{C A^{\prime}}=\frac{F N}{F A^{\prime}}\) …(3) (∵ DN = AB)
यदि अवतल दर्पण का द्वारक बहुत अधिक छोटा हो, तो बिन्दु N दर्पण के ध्रुव (P) के बहुत निकट होगा।
इस दशा में, FN = FP (लगभग)
तथा समीकरण (3) को निम्न प्रकार लिख सकते हैं

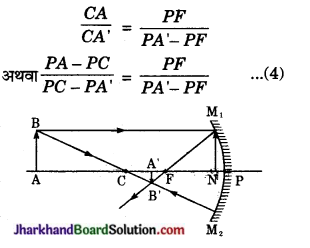
अवतल दर्पण में, चिन्हों के नियमानुसार-
वस्तु की दर्पण के ध्रुव से दूरी PA = – u
प्रतिबिम्ब की दर्पण के ध्रुव से दूरी PA’ = – v
दर्पण की फोकस दूरी PF = – f
दर्पण की वक्रता त्रिज्या PC = – r = 2f
समीकरण (4) में मान रखने पर,
\(\frac{-u-(-2 f)}{-2 f-(-v)}=\frac{-f}{-v-(-f)}\)
अथवा \(\frac{-u+2 f}{-2 f+v}=\frac{-f}{-v+f}\)
-f(-2f + v) = (- v + f)(-u + 2f)
अथवा 2f² – vf = uv – 2vf – uf + 2f²
अथवा uv = uf + vf
दोनों पक्षों में uvf से भाग देने पर,
अवतल दर्पण का सूत्र \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}/latex]

प्रश्न 5.
उत्तल दर्पण के के सम्मुख किसी भी स्थिति में रखी वस्तु के दर्पण द्वारा बने प्रतिबिम्ब की स्थिति, आकार एवं प्रकृति किरण आरेख खींचकर बनाइए।
उत्तर:
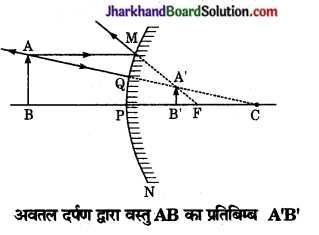
नीचे चित्र में MPN एक उत्तल दर्पण है जिसके सम्मुख मुख अक्ष पर वस्तु AB स्थित है। बिन्दु A से चलने वाली प्रकाश किरणें AM और AQ दर्पण से परावर्तन के पश्चात् FM व CA में चली जाती है जो A से आती हुई प्रतीत होती है। इस प्रकार A’ आभासी प्रतिबिम्ब बनता है। इसी प्रकार AB के विभिन्न बिन्दुओं के अभासी A’B’ ‘के संगत बिन्दुओं पर बनते हैं। अतः उत्तल दर्पण में वस्तु का प्रतिबिम्ब सदैव वस्तु से छोटा, सीधा, आभासी एवं दर्पण के पीछे सदैव फोकस और ध्रुव के मध्य बनता है।

प्रश्न 6.
लेंस द्वारा प्रतिबिम्ब बनाने के नियम लिखो।
उत्तर:
लेंस द्वारा प्रतिबिम्ब बनाने के नियम निम्नलिखित है-

• वह प्रकाश किरण जो लेंस की मुख्य अक्ष के समान्तर आपतित होती है, उत्तल लेंस से अपवर्तन के पश्चात् मुख्य अक्ष की ओर झुककर फोकस F से गुजरती है तथा अवतल लेंस से अपवर्तन के पश्चात् मुख्य अक्ष से दूर हटकर लेंस के फोकस से आती प्रतीत होती है।
• लेंस के प्रकाशिक केन्द्र 0 से गुजरने वाली किरण अपने मार्ग पर ही बिना किसी विचलन के चली जाती है।
• लेंस के फोकस से गुजरने वाली आपतित किरण (उत्तल लेंस में) अथवा एकत्रित प्रतीत होने वाली आपतित किरण (अवतल लेंस में) लेन्स से परावर्तन के पश्चात् मुख्य अक्ष के समान्तर हो जाती है।

लेंस द्वारा किसी वस्तु का प्रतिबिम्ब बनाने के लिए उपर्युक्त तीनों में से किन्हीं दो किरणों का ही उपयोग किया जाता है।

प्रश्न 7.
किरण आरेख द्वारा पूर्ण परावर्तक प्रिज्म का (i) 90° विचलन, (ii) 180° विचलन प्रिज्म के लिए उपयोग बताइये।
उत्तर:
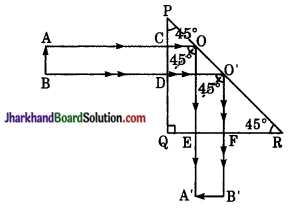
(i) 90° विचलन के लिए पूर्ण परावर्तक का उपयोग – चित्रानुसार जब वस्तु AB, प्रिज्म के सम्मुख रखते हैं तो उससे निकलने वाली प्रिज्म भुजा PQ किरणें AC व BD अत: तल PQ पर लम्बवत् आपतित होती हैं बिना मुड़े सीधे कर्ण PR के बिन्दु 0 एवं O’ पर पड़ती तथा अभिलम्ब के साथ 45° का कोण बनाती हैं। चूँकि 42° होता है अतः इनका पूर्ण परावर्तन हो जाता है।

पूर्ण हो जाता है। पूर्ण परावर्तित किरणें OE व OF क्रान्ति क्रमशः तल OR के बिन्दु E व F पर लम्ब लम्बवत् पड़ती हैं अत: सीधे EA’ व FB’ की दिशा में निकल जाती हैं। इस प्रकार AB का प्रतिबिम्ब A’B’ बनता है जो AB से 90° झुका हुआ है। स्पष्ट है इससे साधारण दर्पण की अपेक्षा अधिक चमकीला प्रतिबिम्ब बनता है। इसलिए इसका उपयोग पेरिस्कोप में समतल दर्पण के स्थान पर करते हैं।

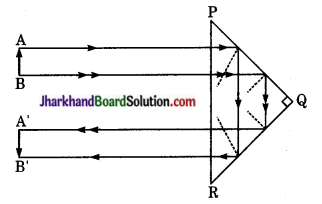
(ii) 180° विचलन के लिए पूर्ण परावर्तक प्रिज्म का उपयोग – चित्रानुसार जब वस्तु AB, प्रिज्म के कर्ण भुजा PR के सम्मुख रखते हैं तो उससे निकलने वाली किरणें PR पर लम्बवत् आपतित होती हैं जिसका (काँच का क्रांतिक कोण 42° होने के कारण) प्रिज्म के फलक PQ व QR पर दो बार पूर्ण आन्तरिक परावर्तन हो जाता है। तथा निर्गत किरण का मार्ग आपतित किरण के विपरीत दिशा में अर्थात् 180° कोण से विचलित हो जाता है। इस प्रकार यह प्रिज्म उल्टे प्रतिबिम्ब को सीधा करने के लिए प्रयुक्त किया जाता है।

प्रश्न 8.
किसी अवतल लेंस द्वारा प्रतिबिम्ब बनने की प्रक्रिया का रेखाचित्र दीजिए।
उत्तर:
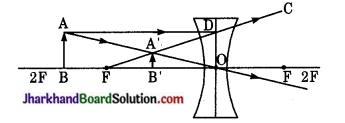
चित्रानुसार, अवतल लेंस के सम्मुख एक वस्तु AB रखी गयी है जिसका प्रतिबिम्ब A’B’ लेंस के सामने वस्तु की ओर लेंस व प्रकाशिक केन्द्र के बीच आभासी, सीधा तथा वस्तु छोटा बनता है। वस्तु को अवतल लेंस के सामने कितनी भी दूरी पर रखें, उसका प्रतिबिम्ब सदैव उसी ओर प्रकाशिक केन्द्र व फोकस के बीच वस्तु से छोटा, सीधा व आभासी बनता है।

प्रश्न 9.
काँच के गुटके का अपवर्तनांक ज्ञात करने की विधि को लिखकर आरेख खींचिए।
उत्तर:
काँच के गुटके का अपवर्तनांक ज्ञात करना – सर्वप्रथम ड्राइंग बोर्ड पर एक सफेद कागज ड्राइंग पिन की सहायता से लगा देते हैं। कागज पर काँच के गुटके की सीमा रेखा ABCD बना दें। अब पृष्ठ AB पर एक बिन्दु O लें तथा AB पर अभिलम्ब N₁ON₂ खींचे। अब रेखा N₁N₂ के साथ बिन्दु पर ∠N₁OX बनाते हुए रेखा OX खींचें। रेखा OX पर दो पिनें P₁ तथा P₂ ऊर्ध्वाधर ठोंक दो।

अब काँच के गुटके को ABCD पर रख दें तथा CD तल पर पिनों P₁ व P₂ के प्रतिबिम्बों को देखते हुए उनके ठीक सीध में दो अन्य पिनें P₃ तथा P₄ पुनः ठोंक दो। इस प्रकार चारों पिनें एक सीध में दिखेंगी। काँच का गुटका हटा देते हैं।

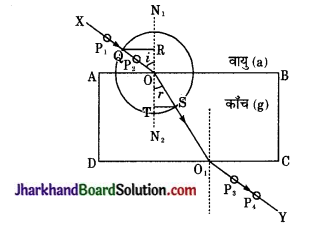
अब पिनों को हटाकर P₃ तथा P₄ को मिला देते हैं जो पृष्ठ CD को O₁ पर मिलती है। बिन्दु O व O₁ को मिला दो। अब O को केन्द्र मानकर किसी त्रिज्या का एक वृत्त बनाया जो OX को Q पर तथा OO₁ को S पर काटती है। अब Q व S से अभिलम्ब N₁ON₂ पर लम्ब OR व ST खींचें। OR व ST की लम्बाई माप लेते हैं।

प्रश्न 10.
प्रकाश के अपवर्तन से क्या तात्पर्य है? यह प्रकाश के परावर्तन से किस प्रकाश भिन्न होता है। जब किसी दूसरे पारदर्शी माध्यम (2) के तल पर आपतित
उत्तर:
किसी एक माध्यम (1) में चलता हुआ प्रकाश जब किसी दूसरे पारदर्शी माध्यम (2) के तल पर आपतित होता है तो आपतित प्रकाश का कुछ अंश, पहले माध्यम से ही वापस लौट जाता है-जिसे प्रकाश परावर्तन कहते हैं।

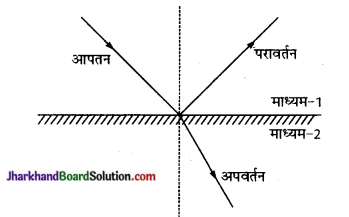
आपतित प्रकाश का अधिकांश भाग दूसरे माध्यम में अपने पहले मार्ग से कुछ विचलित होकर, गमन करता है। एक माध्यम से दूसरे माध्यम में, अपने पूर्व मार्ग से विचलित होकर गमन को प्रकाश का अपवर्तन कहते हैं।

प्रश्न 11.
प्रकाश के अपवर्तन के नियम लिखिए तथा उपयुक्त आरेख बनाकर स्नैल का नियम स्पष्ट कीजिए।
अथवा
प्रकाश के अपवर्तन सम्बन्धी स्नैल के नियम लिखिए तथा समझाइए।
उत्तर:
चित्र में प्रकाश के माध्यम-1 से माध्यम -2 में अपवर्तन को दर्शाया गया है। अपवर्तन बिन्दु 0 पर अभिलम्ब एवं आपतित किरण के बीच बने कोण (i) को आपतन कोण तथा अभिलम्ब एवं अपवर्तित किरण के बीच बने कोण (r) को आयतन कोण कहते हैं।

अपवर्तन के नियमों के अनुसार,
(1) आपतित किरण, अपवर्तित किरण तथा आपतन बिन्दु पर खींचा गया अभिलम्ब, तीनों एक ही समतल में होते हैं।

(2) आपतन कोण (sin i) तथा अपवर्तन कोण (sin r) की ज्या (sin e) परस्पर समानुपाती होते हैं।

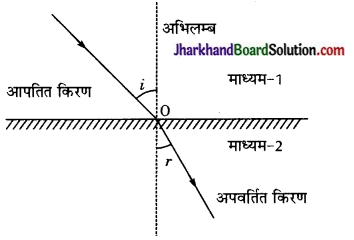
इस नियम को स्नैल का नियम कहते हैं। इसके अनुसार,
sin i ∝ sin r
अथवा [latex]\frac { sin i }{ sin r }\) = n (n एक नियतांक है।)
नियतांक n को पहले माध्यम (1) के सापेक्ष दूसरे माध्यम (2) का अपवर्तनांक कहते हैं तथा प्रतीक ₁n₂ से व्यक्त करते हैं।

आंकिक प्रश्न

प्रश्न 1.
अवतल दर्पण से 2.0 सेमी दूर रखी वस्तु का वास्तविक प्रतिबिम्ब 30 सेमी दूर बनता है। दर्पण की फोकस – दूरी ज्ञात कीजिए।
उत्तर:
अवतल दर्पण के लिए,
वस्तु की दूरी (u) = – 20 सेमी
वास्तविक प्रतिबिम्ब की दूरी
(v) = – 30 सेमी
अवतल दर्पण के सूत्र
\(\frac{1}{f}=\frac{1}{-30}+\frac{1}{-20}\)
\(\frac{1}{f}=\frac{(-20)+(-30)}{600}=\frac{-50}{600}\)
= – \(\frac { 1 }{ 12 }\)
अतः अवतल दर्पण की फोकस-दूरी
(f) = – 12 सेमी।

प्रश्न 2.
एक अवतल दर्पण की फोकस-दूरी 25 सेमी है। दर्पण से $2.0$ सेमी दूरी पर रखी वस्तु के प्रतिबिम्ब की स्थिति एवं प्रकृति ज्ञात किजिए।
उत्तर:
अवतल दर्पण की फोकस-दूरी (f) = – 25 सेमी.
दर्पण से वस्तु की दूरी
(u) = – 20 सेमी.
अवतल दर्पण के सूत्र \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\) से,
\(\frac{1}{v}+\left(-\frac{1}{20}\right)=-\frac{1}{25}+\frac{1}{20}\)
\(\frac{1}{v}=-\frac{1}{25}+\frac{1}{20}\)
\(\frac{1}{v}=\frac{-4+5}{100}=\frac{1}{100}\)
∴ v = 100 सेमी, v का मान धनात्मक है। अत: प्रतिबिम्ब दर्पण के पीछे बनता है। प्रतिबिम्ब का आवर्धन
m = \(\frac { v }{ u }\)
= \(\frac { 100 }{ 20 }\) = 5
अर्थात् प्रतिबिम्ब सीधा तथा वस्तु से 5 गुना बड़ा बनता है। प्रतिबिम्ब दर्पण के पीछे बनने के कारण आभासी हैं। ]

प्रश्न 3.
एक अवतल दर्पण से 30 सेमी दूर रखी वस्तु का तीन गुना बड़ा
(i) आभासी,
(ii) वास्तविक प्रतिबिम्ब प्राप्त होता है। प्रत्येक दशा में अवतल दर्पण की फोकस-दूरी ज्ञात कीजिए।
उत्तर:
(i) आभासी प्रतिबिम्ब के लिए-
अवतल दर्पण से वस्तु की दूरी
(u) = – 30 सेमी
प्रतिबिम्ब का आवर्धन
(m) = + 3
प्रतिबिम्ब का आवर्धन
m = – \(\frac { v }{ u }\) से
v = – m u = – 3 x (- 30)
= – 90 सेमी
अवतल दर्पण के सूत्र \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\) से,
\(\frac{1}{f}=\frac{1}{-30}+\frac{1}{90}\)
\(\frac{-3+1}{90}\)
= \(\frac { -2 }{ 90 }\) = – \(\frac { 1 }{ 45 }\)
अर्थात् अवतल दर्पण की फोकस दूरी
(f) = – 45 सेमी

(ii) वास्तविक प्रतिबिम्ब के लिए-
m = – 3
v = – m u
= – (- 3) x (- 30) = – 90 सेमी
अवतल दर्पण के सूत्र \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\) से,
= – \(\frac{1}{30}-\frac{1}{90}\)
= \(\frac{-3-1}{90}=\frac{-4}{90}\)
f = – \(\frac{90}{4}\) = – 22.5 सेमी
अतः अवतल दर्पण की फोकस-दूरी
(f) = – 22.5 सेमी

प्रश्न 4.
उत्तल दर्पण से 40 सेमी दूर रखी वस्तु का प्रतिबिम्ब 10 सेमी दूर बनता है। उत्तल दर्पण की फोकस-दूरी ज्ञात कीजिए।
उत्तर:
उत्तल दर्पण में,
दर्पण से वस्तु की दूरी
(u) = – 40 सेमी
प्रतिबिम्ब की दूरी
(v) = + 10 सेमी
उत्तल दर्पण के सूत्र \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\) से,
\(\frac{1}{f} =-\frac{1}{40}+\frac{1}{10}\)
= \(\frac{-1+4}{40}=\frac{3}{40}\)
∴ उत्तल दर्पण की फोकस-दूरी
(f) = \(\frac{40}{3}\) = 13.33 सेमी
अतः उत्तल दर्पण की फोकस-दूरी = 13.33 सेमी।

प्रश्न 5.
एक उत्तल दर्पण की फोकस दूरी 20 सेमी है। इस दर्पण से 25 सेमी दूर रखी वस्तु के प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
उत्तर:
उत्तल दर्पण में,
उत्तल दर्पण की फोकस दूरी
(f) = 20 सेमी
वस्तु की दूरी (u) = – 25 सेमी
उत्तल दर्पण के सूत्र \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\) से
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
= \(\frac{1}{20}-\frac{1}{(-25)}\)
= \(\frac{1}{20}+\frac{1}{-25}\)
= \(\frac { 5+4 }{ 100 }\) = \(\frac { 9 }{ 100 }\)
अथवा प्रतिबिम्ब की स्थिति
v = \(\frac { 100 }{ 9 }\)
= 11.11 सेमी
अतः प्रतिबिम्ब उत्तल दर्पण के पीछे 11.11 सेमी पर बनता है।

प्रश्न 6.
एक उत्तल दर्पण से 25 सेमी दूर रखी वस्तु का प्रतिबिम्ब वस्तु की लम्बाई का आधा होता है। दर्पण की फोकस दूरी ज्ञात कीजिए।
उत्तर:
उत्तल दर्पण में,
वस्तु की दूरी (u) = -25 सेमी.
प्रतिबिम्ब की लम्बाई

अथवा दर्पण की फोकस दूरी f = 25 सेमी

प्रश्न 7.
6 सेमी लम्बाई की एक कील उत्तल दर्पण के सामने 20 सेमी दूर रखी है। यदि इस दर्पण की फोकस – दूरी 10 सेमी हो, तो कील के प्रतिबिम्ब की स्थिति एवं लम्बाई ज्ञात कीजिए।
उत्तर:
उत्तल दर्पण में,
कील की लम्बाई (O) = 6 सेमी
कील की दूरी (u) = – 20 + 10 सेमी
फोकस दूरी (f) = + 10 सेमी
∴ उत्तल दर्पण के सूत्र \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\) से
\(\frac{1}{10}=-\frac{1}{20}+\frac{1}{v}\)
अथवा \(\frac{1}{v}=\frac{1}{10}+\frac{1}{20}\)
= \(\frac{2+1}{20}=\frac{3}{20}\)
अथवा v = \(\frac { 20 }{ 3 }\)
= 6.67 सेमी दर्पण के पीछे
अब आवर्धन m = \(\frac { v }{ u }\) = \(\frac { 20/3 }{ 20 }\)
= \(\frac { 1 }{ 3 }\) = तथा m = \(\frac { I }{ O }\)
∴ प्रतिबिम्ब की लम्बाई (I) = m x 0 = \(\frac { 1 }{ 3 }\) x 6 = 2 सेमी।
अतः प्रतिबिम्ब दर्पण के पीछे 6.67 सेमी दूरी पर 2 सेमी लम्बाई का बनता है।

प्रश्न 8.
एक वस्तु 30 सेमी वक्रता त्रिज्या वाले अवतल दर्पण से 25 सेमी की दूरी पर रखी है। प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
उत्तर:
अवतल दर्पण में,
वस्तु की दूरी (u) = 25 सेमी
वक्रता त्रिज्या (R) = 30 सेमी
फोकस दूरी (f) = \(\frac { R }{ 2 }\) = \(\frac { -30 }{ 2 }\) = – 15 सेमी
∴ उत्तल दर्पण के सूत्र \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\) से,
\(\frac{1}{v}=\frac{1}{-15}-\frac{1}{-25}\)
= \(-\frac{1}{15}+\frac{1}{25}\)
= \(\frac{-25+15}{375}=-\frac{10}{375}\)
v = – \(\frac { 375 }{ 10 }\)
= – 37.5
∴ प्रतिबिम्ब की दूरी (v) = 37.5 सेमी दर्पण के सामने।

प्रश्न 9.
एक 10 सेमी फोकस दूरी वाले अवतल दर्पण से कितनी दूरी पर कोई वस्तु रखी जाय कि उसका 5 गुना बड़ा प्रतिबिम्ब बने जबकि प्रतिबिम्ब (i) आभासी, (ii) वास्तविक हो।
उत्तर:
अवतल दर्पण के लिए,
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
(i) वास्तविक प्रतिबिम्ब वस्तु तथा फोकस सभी दर्पण के बायीं ओर होते हैं इसलिए निर्देशांक ज्यामिति की चिन्ह परिपाटी के अनुसार ७, ७ तथा सब ऋणात्मक होंगे। अतः आवर्धन
(m) = 5 = \(\frac { v }{ u }\)
∴ प्रतिबिम्ब की दूरी (v) = 5u
अव तल दर्पण की फोकस – दूरी
(f) = – 10 सेमी
∴ \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
या, \(-\frac{1}{5 u}+\frac{1}{u}=-\frac{1}{10}\)
या, \(\frac{-1+5}{5 u}=-\frac{1}{10}\)
या, \(\frac{4}{5 u}=-\frac{1}{10}\)
5u = – 40
u = \(\frac { -40 }{ 5 }\)
∴ u = – 8 सेमी
अतः वस्तु से पाँच गुना बड़ा वास्तविक प्रतिबिम्ब प्राप्त करने के लिए वस्तु को अवतल दर्पण से 8 सेमी दूर रखना होगा।

(ii) यदि आभासी प्रतिबिम्ब बनेगा तो वह अवतल दर्पण के पीछे बनेगा। ऐसी दशा में धनात्मक होगा।
अवतल दर्पण के सूत्र से
\(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
∴ \(\frac{1}{5 u}+\frac{1}{u}=\frac{1}{-10}\)
\(\frac{1+5}{5 u}=\frac{1}{-10}\)
∴ \(\frac{6}{5u}=\frac{1}{-10}\)
5u = – 60
या u = – 12 सेमी।
∴ वस्तु का पाँच गुना बड़ा आभासी प्रतिबिम्ब अवतल दर्पण द्वारा प्राप्त करने के लिए वस्तु दर्पण के ध्रुव से 12 सेमी की दूरी पर रखना होगा।

प्रश्न 10.
एक उत्तल दर्पण 20 सेमी वक्रता त्रिज्या वाला है। इसके सामने कोई वस्तु रखी जाती है तो उसका प्रतिबिम्ब वस्तु के आधे आकार का बनता है। वस्तु तथा प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
उत्तर:
उत्तल दर्पण की वक्रता-त्रिज्या = 20 सेमी
प्रश्नानुसार, आवर्धन
m = \(\frac { v }{ vu}\) = \(\frac { 1 }{ 2 }\)
अथवा u = 2v
फोकस – दूरी (f) = \(\frac { R }{ 2 }\) = + \(\frac { 20 }{ 2 }\) = 10 सेमी
चूँकि उत्तल दर्पण में प्रतिबिम्ब दर्पण के पीछे बनता है अतः v का चिन्ह धनात्मक एवं u का चिन्ह ऋणात्मक होगा।
उत्तल दर्पण के सूत्र \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
\(\frac { 1 }{ v }\) + \(\frac { 1 }{ -2v }\) = \(\frac { 1 }{ 10 }\)
\(\frac { 1 }{ v }\) – \(\frac { 1 }{ v }\) = \(\frac { 1 }{ 10 }\)
\(\frac { 2-1 }{ 2v }\) = \(\frac { 1 }{ 10 }\)
अथवा \(\frac { 1 }{ 2v }\) = \(\frac { 1 }{ 10 }\)
∴ v = \(\frac { 10 }{ 2 }\) = 5 सेमी दर्पण के पीछे
तथा u = 2v = 5 x 2
= 10 सेमी दर्पण के सामने।

प्रश्न 11.
एक वस्तु अवतल दर्पण से 15 सेमी की दूरी पर रखी गयी है। इसका प्रतिबिम्ब वस्तु की ओर 30 सेमी की दूरी पर बनता है। यदि वस्तु 8 सेमी की दूरी पर रहे तो प्रतिबिम्ब का स्थान कहाँ होगा? उत्तर:
पहली दशा में वस्तु की दूरी (u) = 15 सेमी, प्रतिबिम्ब की दूरी (v) = – 30 सेमी
अतः अवतल दर्पण के सूत्र \(\frac { 1 }{ f }\) = \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) से,
\(\frac{1}{f}=\frac{1}{-30}+\frac{1}{-15}\)
= \(\frac{-15-30}{450}=\frac{-45}{450}=\frac{1}{-10}\)
दूसरी दशा में वस्तु की दूरी (u) = 8 सेमी, प्रतिबिम्ब की दूरी (u) = ?
अतः \(\frac{1}{v}+\frac{1}{-8}=\frac{1}{-10}\)
अथवा \(\frac{1}{v}=\frac{1}{8} \frac{1}{-10}=\frac{8-10}{80}=\frac{1}{40}\)
v = + 40 सेमी
अतः प्रतिबिम्ब दर्पण के पीछे 40 सेमी दूरी पर बनेगा।

प्रश्न 12.
12 सेमी फोकस दूरी वाले अवतल दर्पण के सामने 4 सेमी लम्बी वस्तु रखी है। इसका 1 सेमी लम्बा प्रतिबिम्ब बनता है तो वस्तु की स्थिति ज्ञात कीजिए।
उत्तर:
अवतल दर्पण की फोकस दूरी f = 12 सेमी
वस्तु की लम्बाई (O) = 4 सेमी
आवर्धन (m) = \(\frac { I }{ O }\) = \(\frac { 1 }{ 4 }\) = \(\frac { v }{ u }\)
अथवा v = \(\frac { u }{ 4 }\); f = – 12 सेमी
अवतल दर्पण में छोटा प्रतिबिम्ब वस्तु की ही ओर बनता है अतः u तथा v दोनों के चिन्ह (-) होंगे। अवतल दर्पण के सूत्र
\(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) से,
\(\frac{1}{-(u / 4)}+\frac{1}{-u}=-\frac{1}{12}\)
अथवा \(\frac { 4 }{ u }\) – \(\frac { 1 }{ u }\) = – \(\frac { 1 }{ 12 }\) या \(\frac { 5 }{ u }\) = – \(\frac { 1 }{ 12 }\)
सरल करने पर u = 60 सेमी
अतः वस्तु दर्पण के सामने 60 सेमी दूर स्थित है।

प्रश्न 13.
50 सेमी फोकस दूरी वाले अवतल दर्पण के सामने 25 सेमी की दूरी पर रखी वस्तु के दर्पण से बने प्रतिविम्ब की स्थिति ज्ञात कीजिए।
उत्तर:
अवतल दर्पण में.
वस्तु की दूरी (u) = – 25 सेमी
फोकस – दूरी (f) = – 50 सेमी
प्रतिबिम्ब की दूरी (v) = ?
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
\(\frac{1}{-50}=\frac{1}{v}+\frac{1}{-25}\)
या, \(\frac{1}{v}=\frac{1}{25}-\frac{1}{50}=\frac{2-1}{50}=\frac{1}{50}\)
\(\frac { 1 }{ v }\) = \(\frac { 1 }{ 50 }\)
∴ v = 50 सेमी, दर्पण के पीछे प्रतिबिम्ब बनेगा।

प्रश्न 14.
10 सेमी फोकस दूरी के उत्तल दर्पण एक वस्तु को 30 सेमी की दूरी पर रखने से प्रतिविम्ब कहाँ बनेगा? यदि वस्तु की लम्बाई 6 सेमी हो तो प्रतिबिम्ब की लम्बाई कितनी होगी?
उत्तर:
उत्तल दर्पण में,
f = + 10 सेमी
वस्तु की दूरी (u) = – 30 सेमी,
v = ?, O = 6 सेमी, I = ?

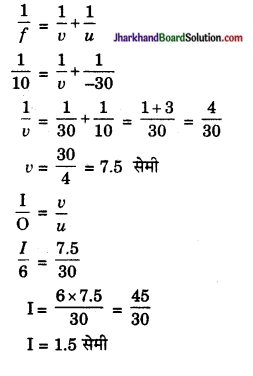
प्रश्न 15.
एक अवतल दर्पण की फोकस दूरी 5 सेमी है। इसके सामने 10 सेमी की दूरी पर रखी वस्तु का प्रतिबिम्ब कहाँ पर बनेगा? क्या यह वास्तविक होगा।
उत्तर:
अवतल दर्पण की फोकस दूरी (f) = – 5 सेमी
वस्तु की दूरी (u) = 10 सेमी
प्रतिबिम्ब की दूरी (v) = ?
∴ \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) से,
\(\frac{1}{v}-\frac{1}{10}=\frac{1}{-5}\)
\(\frac{1}{v}=-\frac{1}{5}+\frac{1}{10}=-\frac{1}{10}\)
v = – 10 सेमी
अर्थात् प्रतिबिम्ब दर्पण से 10 सेमी दूर वस्तु की ओर बनेगा। प्रतिबिम्ब वास्तविक होगा
दर्पण से 10 सेमी दूर वस्तु की ओर, वास्तविक।

प्रश्न 16.
यदि वायु के सापेक्ष जल का एवं शीशे का अपवर्तनांक क्रमशः 4/3 एवं 3/2 हो तो शीशे के सापेक्ष जल के अपवर्तनांक की गणना कीजिए।
उत्तर:
दिया है –

प्रश्न 17.
जल में प्रकाश की चाल 2.25 x 10⁸ मी/से है। यदि जल का अपवर्तनांक 4/3 हो तो निर्वात् में प्रकाश की चाल ज्ञात कीजिए।
उत्तर:

प्रश्न 18.
जल और काँच के अपवर्तनांक क्रमशः 1.35 एवं 1.50 हैं। यदि प्रकाश किरणें काँच से जल में जा रही हों, तो काँच के सापेक्ष जल का अपवर्तनांक ज्ञात कीजिए।
उत्तर:

प्रश्न 19.
यदि प्रिज्म का प्रिज्म कोण 60° तथा न्यूनतम विचलन कोण 36° हो तो प्रिज्म के पदार्थ का अपवर्तनांक ज्ञात कीजिए।
उत्तर:

प्रश्न 20.
वायु के सापेक्ष किसी द्रव का क्रान्तिक कोण 45° है। उस द्रव का अपवर्तनांक ज्ञात कीजिए।
उत्तर:
वायु के सापेक्ष द्रव का क्रान्तिक कोण (C) = 45°

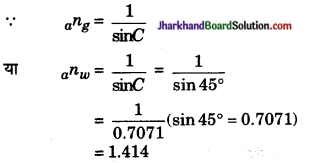
प्रश्न 21.
यदि वायु के सापेक्ष किसी पारदर्शी द्रव का अपवर्तनांक 1.25 है तथा काँच का अपवर्तनांक 1.5 है, तो द्रव के सापेक्ष काँच के अपवर्तनांक की गणना कीजिए।
उत्तर:
वायु के सापेक्ष द्रव का अपवर्तनांक
= 1.25 (_an_w)
वायु के सापेक्ष काँच का अपवर्तनांक= 1.5 (_an_g)
तो द्रव के सापेक्ष काँच का अपवर्तनांक
= \({ }_w n_g=\frac{{ }_a n_g}{{ }_a n_w}=\frac{1.5}{1.25}\) = 1.2
= 1.2

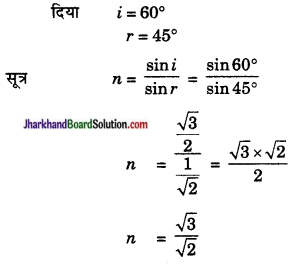
प्रश्न 22.
संलग्न चित्र के अनुसार प्रकाश की किरण वायु से किसी माध्यम में प्रवेश करती है। वायु के सापेक्ष माध्यम का अपवर्तनांक ज्ञात कीजिए।

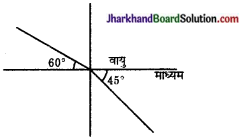
उत्तर:

बहुविकल्पीय प्रश्न

1. एक अवतल दर्पण की वक्रता त्रिज्या 20 सेमी है। इसकी फोकस दूरी होगी-
(a) 10 सेमी
(b) 15 सेमी
(c) 10 सेमी
(d) 20 सेमी
उत्तर:
(a) 10 सेमी

2. उस उत्तल दर्पण की वक्रता त्रिज्या क्या होगी जिसकी फोकस दूरी 10 सेमी है?
(a) 5 सेमी
(b) 10 सेमी
(c) 20 सेमी
(d) 30 सेमी
उत्तर:
(c) 20 सेमी

3. गोलीय दर्पण की फोकस दूरी और वक्रता त्रिज्या में सम्बन्ध होता है-
(a) f = \(\frac { R }{ 2 }\)
(b) f = 2R
(c) R = \(\frac { f }{ 2 }\)
(d) f = R
उत्तर:
(a) f = \(\frac { R }{ 2 }\)

4. 10 सेमी फोकस दूरी वाले अवतल दर्पण के सामने 20 सेमी पर रखी वस्तु का प्रतिबिम्ब बनेगा-
(a) दर्पण के पीछे
(b) फोकस पर
(c) दर्पण और फोकस के बीच
(d) दर्पण के वक्रता केन्द्र पर
उत्तर:
(d) दर्पण के वक्रता केन्द्र पर

5. एक अवतल दर्पण की वक्रता त्रिज्या 12 सेमी है, तो इसकी फोकस दूरी होगी-
(a) 12 सेमी
(b) + 6 सेमी
(c) 24 सेमी
(d) 6 सेमी
उत्तर:
(d) 6 सेमी

6. किसी अवतल दर्पण के सामने वस्तु कहाँ रखी जाय कि प्रतिविम्ब आभासी, सीधा बड़ा बने?
(a) फोकस तथा दर्पण के बीच
(b) f दूरी तथा 2f के बीच
(c) 2f दूरी पर
(d) कहीं भी
उत्तर:
(a) फोकस तथा दर्पण के बीच

7. उत्तल दर्पण के सामने रखी वस्तु का प्रतिबिम्ब बनता है-
(a) वस्तु की स्थिति पर ही
(b) दर्पण के सामने वस्तु की स्थिति से दुगुनी दूरी पर
(c) दर्पण के सामने वस्तु की स्थिति से आधी दूरी पर
(d) दर्पण के पीछे
उत्तर:
(d) दर्पण के पीछे

8. एक उत्तल दर्पण की फोकस दूरी 12 सेमी है दर्पण के उत्तल पृष्ठ की त्रिज्या होगी-
(a) 6 सेमी
(b) 12 सेमी
(c) 18 सेमी
(d) 24 सेमी
उत्तर:
(d) 24 सेमी

9. इनमें से कौन-सा दर्पण वस्तु छोटा व आभासी प्रतिविम्ब बनाता है?
(a) समतल
(b) अवतल
(c) उत्तल
(d) उपर्युक्त तीनों
उत्तर:
(c) उत्तल

10. एक व्यक्ति दर्पण में अपना सीधा और बड़ा प्रतिबिम्ब देखता है। यह दर्पण है-
(a) उत्तल
(b) अवतल
(c) समतल
(d) उपर्युक्त तीनों
उत्तर:
(b) अवतल

11. उत्तल दर्पण से बना प्रतिबिम्ब होता है सदैव-
(a) वस्तु से छोटा
(b) वस्तु से बड़ा
(c) समान आकार का
(d) वास्तविक
उत्तर:
(a) वस्तु से छोटा

12. किसका दृष्टि क्षेत्र सबसे अधिक होता है?
(a) समतल दर्पण
(b) उत्तल दर्पण
(c) अवतल दर्पण
(d) उत्तल लेंस
उत्तर:
(c) अवतल दर्पण

13. यदि किसी वस्तु को दर्पण के निकट रखने पर सीधा प्रतिबिम्ब बने तथा दूर रखने पर वास्तविक प्रतिबिम्ब बने तो वह दर्पण होगा-
(a) अवतल
(b) उत्तल
(c) समतल
(d) उत्तल अथवा समतल
उत्तर:
(a) अवतल

14. किसी अवतल दर्पण द्वारा आभासी, सीधा तथा आवर्धित प्रतिबिम्ब बनता है। वस्तु की स्थिति होगी-
(a) ध्रुव व फोकस के बीच
(b) फोकस तथा वक्रता केन्द्र
(c) वक्रता केन्द्र पर
(d) वक्रता केन्द्र से पीछे
उत्तर:
(b) फोकस तथा वक्रता केन्द्र

15. एक अवतल दर्पण की फोकस दूरी 10 सेमी है। दर्पण की वक्रता त्रिज्या होगी?
(a) 10 सेमी
(b) 20 सेमी
(c) 30 सेमी
(d) 40 सेमी
उत्तर:
(b) 20 सेमी

16. किसी अवतल दर्पण की फोकस दूरी 15 सेमी है। उसकी वक्रता त्रिज्या होगी-
(a) 15 सेमी
(b) 30 सेमी
(c) 45 सेमी
(d) 60 सेमी
उत्तर:
(b) 30 सेमी

17. समतल दर्पण की फोकस दूरी होती है-
(a) शून्य
(b) अनन्त
(c) 25 सेमी
(d) -25 सेमी
उत्तर:
(b) अनन्त

18. फोकस दूरी व वक्रता त्रिज्या के बीच सम्बन्ध है-
(a) f = r
(b) f = \(\frac { 1 }{ r }\)
(c) 2f = r
(d) f = 2r
उत्तर:
(c) 2f = r

19. एक अवतल दर्पण की वक्रता त्रिज्या 15 सेमी है। इसकी फोकस दूरी होगी-
(a) 15 सेमी
(b) 7.5 सेमी
(c) + 30 सेमी
(d) 7.5 सेमी
उत्तर:
(b) 7.5 सेमी

20. समतल दर्पण के सामने एक वस्तु दर्पण से 10 सेमी की दूरी पर रखी गयी है। दर्पण से प्रतिबिम्ब की दूरी होगी-
(a) 5 सेमी
(b) 10 सेमी
(c) 20 सेमी
(d) 0 सेमी
उत्तर:
(b) 10 सेमी

21. उत्तल दर्पण से प्रतिबिम्ब सदैव बनता है-
(a) वक्रता केन्द्र तथा फोकस के बीच
(b) वक्रता केन्द्र तथा अनन्त के बीच
(c) ध्रुव व फोकस के बीच
(d) कहीं भी बन सकता है।
उत्तर:
(a) वक्रता केन्द्र तथा फोकस के बीच

22. यदि आपतन कोण 42° तथा अपवर्तन कोण 30° हो तब अपवर्तित किरण विचलित होती है-
(a) 12°
(b) 72°
(c) 1.4°
(d) \(\frac { sin 45° }{ sin 30° }\)
उत्तर:
(a) 12°

23. वायु के सापेक्ष काँच का अपवर्तनांक 3/2 है। वायु प्रकाश की चाल 3 x 10⁸ मी/सेकण्ड है। काँच में प्रकाश की चाल होगी-
(a) 1.5 x 10⁸ मी/सेकण्ड
(b) 2 x 10⁸ मी/सेकण्ड
(c) 3 x 10⁸ मी/सेकण्ड
(d) 4.5 x 10⁸ मी/सेकण्ड
उत्तर:
(b) 2 x 10⁸ मी/सेकण्ड

24. जब एक श्वेत प्रकाश की किरण काँच से बने किसी प्रिज्म से गुजरती है, तो किस रंग की किरण के लिए सबसे अधिक विचलन होता है-
(a) पीला
(b) बैंगनी
(c) लाल
(d) हरा
उत्तर:
(b) बैंगनी

25. यदि वायु के सापेक्ष काँच का अपवर्तनांक 1.5 है तो काँच के सापेक्ष वायु का अपवर्तनांक होगा-
(a) 3.00
(b) 1.50
(c) 0.75
(d) 0.67
उत्तर:
(d) 0.67

रिक्त स्थानों की पूर्ति कीजिए

1. एक काँच की स्लैब की क्षमता …………………. होती है।
2. एक लेंस जो बीच में से मोटा और किनारों पर से पतला होता है …………………. लेंस कहलाता है।
3. एक मोटे लेंस की फोकस दूरी कम होती है। इसकी क्षमता …………………. होगी।
4. एक उत्तल लेंस की दक्षता का चिन्ह ………………….।
5. एक अवतल लेंस की क्षमता का चिन्ह …………………. होती है।

उत्तर:

1. शून्य
2. उत्तल
3. अधिक
4. धनात्मक होता है।
5. – 0.5 D
6. धनात्मक।