Jharkhand Board JAC Class 9 Maths Important Questions Chapter 10 वृत्त Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 10 वृत्त
प्रश्न 1.
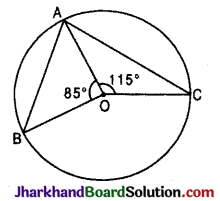
चित्र में, ∠BAC का मान होगा :
(A) 80°
(B) 160°
(C) 90°
(D) 200°
हल :
∠BOC + ∠BOA + ∠COA = 360° (बिन्दु O पर बने कोणों का योग )
⇒ ∠BOC + 85° + 115° = 360°
⇒ ∠BOC + 200° = 360°
∠BOC = 360° – 200° = 160°.
केन्द्र पर अन्तरित कोण वृत्त की परिधि पर बने कोण का दोगुना होता है।
∴ ∠BOC = 2∠BAC
⇒ ∠BAC = \(\frac {∠BOC}{2}\) = \(\frac {160°}{2}\)
∴ ∠BAC = 80°
अतः सही विकल्प ‘A’ है।
![]()
प्रश्न 2.
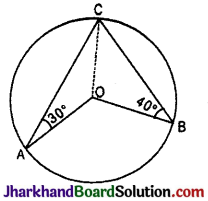
चित्र में, यदि वृत्त का केन्द्र O हो, तो ∠AOB का मान होगा :
(A) 70°
(B) 110°
(C) 120°
(D) 140°.
हल :
C को O से मिलाने पर
ΔAOC में, AO = OC (समान वृत्त की त्रिज्याएँ)
⇒ ∠OAC = ∠OCA
∴ ∠OCA = 30°
इसी प्रकार OB = OC
∠OBC = ∠OCB = 40°
∠ACB = ∠OCA + ∠OCB = 30° + 40° = 70°
∠AOB = 2ACB (वृत्त के केन्द्र पर अन्तरित कोण)
∠AOB = 2 × 70° = 140°
अत: सही विकल्प ‘D’ है।
प्रश्न 3.
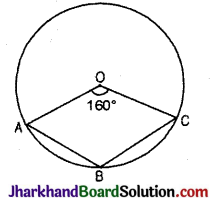
चित्र में, यदि वृत्त का केन्द्र O हो और ∠AOC = 160° हो, तो ∠ABC का मान होगा :
(A) 160°
(B) 80°
(C) 200°
(D) 100°.
हल :
दिया है,
लघु ∠AOC = 160°
दीर्घ ∠AOC = 360°- लघु ∠AOC
= 360° – 160° = 200°
दीर्घ ∠AOC = 2∠ABC (वृत्त के केन्द्र पर अन्तरित कोण)
⇒ ∠ABC = \(\frac {दीर्घ ∠AOC}{2}\)
∴ ∠ABC = \(\frac {200°}{2}\) = 100°
अत: सही विकल्प ‘D’ है।
![]()
प्रश्न 4.
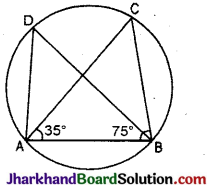
चित्र में, यदि ∠ABC = 75° और ∠BAC = 35° हो, तो ∠ADB होगा :
(A) 40°
(B) 110°
(C) 70°
(D) 75°.
हल :
ΔABC में,
∠ABC + ∠BAC + ∠BCA = 180°, (Δ के अन्तः कोणों का योग)
⇒ 75° + 35° + ∠BCA = 180°
⇒ 110° + ∠BCA = 180°
∴ ∠BCA = 180° – 110° = 70°
∴ ∠ADB = ∠BCA (एक ही वृत्तखण्ड के कोण)
∠ADB = 70°
अत: सही विकल्प ‘C’ है।
प्रश्न 5.
चित्र में x का मान होगा :
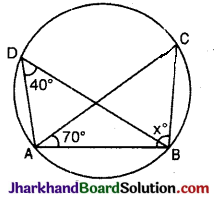
(A) 40°
(B) 70°
(C) 110°
(D) 90°
हल :
⇒ ∠ADB = ∠ACB = 40°
(एक ही वृत्तखण्ड के कोण)
∴ ∠ACB = 40°
[∵ ∠ADB = 40° दिया है ] (Δ के अन्तः कोणों का योग)
अब ΔABC में,
∠ABC + ∠ACB + ∠BAC = 180°
⇒ x° + 40° + 70° = 180°
⇒ x° + 110° = 180°
x° = 180° – 110° = 70°
अतः सही विकल्प ‘B’ है।
![]()
प्रश्न 6.
चित्र में, ABCD एक चक्रीय चतुर्भुज है। यदि ∠D = 120° हो, तो ∠CBE होगा :
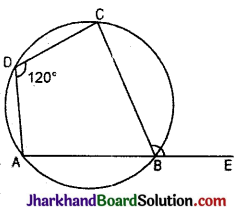
(A) 120°
(B) 60°
(C) 180°
(D) 90°.
हल :
∵ चक्रीय चतुर्भुज का बहिष्कोण उसके अन्तराभिमुख कोण के बराबर होता है।
∴ ∠CBE = ∠ADC = 120°
अत: सही विकल्प ‘A’ है।
प्रश्न 7.
चित्र में, यदि A, B, C और D एक चक्रीय चतुर्भुज के शीर्ष हों, तो ∠x का मान होगा :
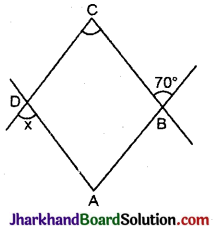
(A) 70°
(B) 35°
(C) 110°
(D) 100°.
हल :
∵ ∠CBA + 70° = 180°, (रैखिक युग्म कोण)
∴ ∠CBA = 180° – 70° = 110°
∵ ABCD चक्रीय चतुर्भुज है।
हम जानते हैं कि चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° होता है।
अतः ∠CBA + ∠CDA = 180°
⇒ 110° + ∠CDA = 180°
∴ ∠CDA = 180° – 110° = 70°
परन्तु ∠x + ∠CDA = 180° (रैखिक युग्म कोण)
⇒ ∠x + 70° = 180°
∴ ∠x = 180° – 70° = 110°
‘अतः सही विकल्प ‘C’ है।
![]()
प्रश्न 8.
यदि वृत्त का व्यास दो जीवाओं में से प्रत्येक समद्विभाजित करे तो जीवाएँ होंगी :
(A) समान्तर
(B) लम्बवत्
(C) प्रतिच्छेदी
(D) इन में से कोई नहीं।
हल :
सही विकल्प ‘A’ है।
प्रश्न 9.
यदि सर्वांगसम वृत्तों में दो चाप सर्वांगसम हों, तो उनकी संगत जीवाएँ होंगी :
(A) समान्तर
(B) बराबर
(C) लम्बवत्
(D) प्रतिच्छेदी ।
हल :
सही विकल्प ‘B’ है।
प्रश्न 10.
एक वृत्त में केन्द्र से समान दूरी पर स्थित जीवाएँ एक-दूसरे की होती हैं :
(A) दोगुनी
(B) तिगुनी
(C) आधी
(D) बराबर ।
हल :
सही विकल्प ‘D’ है।
प्रश्न 11.
एक वृत्त के किसी चाप का डिग्री माप 180° है, वह चाप है :
(A) दीर्घ चाप
(B) लघु चाप
(C) वृत्त
(D) अर्द्धवृत्त ।
हल :
सही विकल्प ‘D’ है।
![]()
प्रश्न 12.
तीन संरेखीय बिन्दुओं से गुजरने वाले वृत्तों की संख्या है :
(A) एक
(B) दो
(C) शून्य
(D) अनन्त ।
हल :
सही विकल्प ‘C’ है।
प्रश्न 13.
यदि किसी वृत्त में चाप AB = चाप BA हो, तो
(A) दीर्घ चाप
(B) लघु चाप
(C) अर्द्ध वृत्त
(D) वृत्त ।
हल :
सही विकल्प ‘C’ है।
प्रश्न 14.
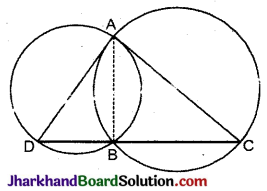
आकृति में, AB वृत्त का एक व्यास है और CD त्रिज्या के बराबर एक जीवा है। AC और BD बढ़ाये जाने पर बिन्दु E पर मिलती हैं। सिद्ध कीजिए कि ∠AEB = 60° है।
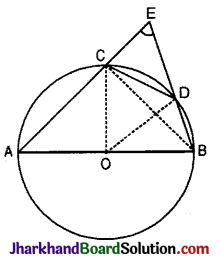
हल :
OC, OD और BC को मिलाया। त्रिभुज ODC एक समबाहु त्रिभुज है।
[क्योंकि OC = OD त्रिज्याएँ हैं तथा CD = त्रिज्या (दिया है)]
∴ ∠COD = 60°
अब ∠CBD = \(\frac {1}{2}\)∠COD
= \(\frac {1}{2}\) × 60°
∴ ∠CBD = 30° ……(i)
∵ AB वृत्त का व्यास है तथा ∠ACB अर्द्धवृत्त में बना कोण है।
∴ ∠ACB = 90°
∴ ∠BCE = 180° – ∠ACB
= 180° – 90°
∴ ∠BCE = 90° ……(ii)
हम जानते हैं ΔBCE से,
∠CBD + ∠BCE + ∠CEB = 180°
∴ ∠CEB = 180° – ∠CBD – ∠BCE
समीकरण (i) व (ii) से मान रखने पर,
∠CEB = 180° – 30° – 90°
∴ ∠CEB = 60°
अर्थात् ∠AEB = 60°
इति सिद्धम् ।
![]()
प्रश्न 15.
दो वृत्त दो बिन्दुओं A और B पर प्रतिच्छेद करते हैं। AD और AC दोनों वृत्तों के व्यास हैं। सिद्ध कीजिए कि बिन्दु B, रेखाखण्ड DC पर स्थित हैं।
हल :
AB को मिलाया।
∠ABD = 90°
(अर्द्धवृत्त में बना कोण) …………..(i)
∠ABC = 90°
(अर्द्धवृत्त में बना कोण) ………(ii)
समीकरण (i) व (ii) को जोड़ने पर,
∠ABD + ∠ABC = 90° + 90°
∴ ∠ABD + ∠ABC = 180°
अत: DBC एक सरल रेखा है।
अत: B, रेखाखण्ड DC पर स्थित है । इति सिद्धम् ।
प्रश्न 16.
सिद्ध कीजिए कि किसी चक्रीय चतुर्भुज के अन्तः कोणों के समद्विभाजकों से बना चतुर्भुज (यदि सम्भव हो) चक्रीय होता है।
हल :
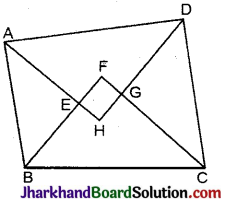
दिया है : ABCD एक चक्रिय चतुर्भुज है, जिसके अन्तः कोण A, B, C और D समद्विभाजक क्रमशः AH, BF, CF और DH
चतुर्भुज EFGH बनाते हैं।
∠ABE = ∠AEB + ∠EAB = 180°
∠AEB = 180°- (∠ABE + ∠EAB) ………..(i)
सिद्ध करना है : EFGH चक्रीय चतुर्भुज है।
उपपत्ति : ΔABE में,
∵ ∠ABE = \(\frac {1}{2}\)∠B (दिया है) … (ii)
∠EAB = \(\frac {1}{2}\)∠A (दिया है) … (iii)
∠AEB = ∠FEH
(शीर्षाभिमुख कोण) …(iv)
समीकरण (i) मैं (ii), (iii) व (iv) से मान रखने पर,
∠FEH = 180° – \(\frac {1}{2}\)(∠A + ∠B)
इसी प्रकार,
∠FGH = 180° – \(\frac {1}{2}\)(∠C + ∠D)
अतः
∠FEH + ∠FGH = 180° – \(\frac {1}{2}\)(∠A + ∠B) + 180° – \(\frac {1}{2}\)(∠C + ∠D)
= 360° – \(\frac {1}{2}\)(∠A + ∠B + ∠C + ∠D)
= 360° – \(\frac {1}{2}\) × 360°
= 360° – 180°= 180°
अतः ∠FEH + ∠FGH = 180°
[चतुर्भुज के सम्मुख कोण]
इसी प्रकार ∠EFG + ∠EHG = 180°
[चतुर्भुज के सम्मुख कोण]
अतः EFGH एक चक्रीय चतुर्भुज है । इति सिद्धम् ।
![]()
प्रश्न 17.
सिद्ध कीजिए कि एक समद्विबाहु त्रिभुज की किसी भी समान भुजा को व्यास मानकर खींचा गया वृत्त, आधार को समद्विभाजित करता है।
हल :
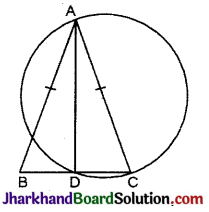
दिया है : समद्विबाहु ΔABC में AB = AC और व्यास AC पर खींचा गया वृत्त आधार BC को D बिन्दु पर प्रतिच्छेदित है।
सिद्ध करना है : BD = CD.
उपपत्ति : AC को व्यास मानकर वृत्त खींचा गया है और ∠ADC अर्द्धवृत्त का कोण है,
अत: ∠ADC = 90°
अब ΔABD और ΔACD से,
AB = AC (दिया है)
AD = AD (उभयनिष्ठ)
∠ADB = ∠ADC (समकोण)
∴ ΔABD ≅ ΔACD (SAS नियम से)
∴ BD = CD. इति सिद्धम् ।
प्रश्न 18.
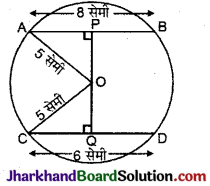
चित्र में, वृत्त का केन्द्र O एवं त्रिज्या 5 सेमी है। यदि OP ⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 सेमी और CD = 6 सेमी हो, तो PQ ज्ञात कीजिए।
हल :
दिया है, OP ⊥ AB एवं OQ ⊥ CD
चूँकि जीवा पर केन्द्र से डाला गया लम्ब जीवा को समद्विभाजित करता है।
अत: AP = PB = \(\frac {1}{2}\)AB = 4 सेमी
तथा CQ = QD = \(\frac {1}{2}\)CD = 3 सेमी
और OA = OC = 5 सेमी (त्रिज्याएँ)
ΔOPA में, बौधायन प्रमेय से,
या OP² = OA² – AP²
OP² = 5² – 4² = 25 – 16 = 9
∴ OP = 3 सेमी
इसी प्रकार ΔOQC में,
OQ² = OC² – CQ²
OQ² = 5² – 3²
= 25 – 9 = 16
∴ OQ = 4 सेमी
अतः PQ = OP + OQ
= 3 + 4 = 7 सेमी।
![]()
प्रश्न 19.
सिद्ध कीजिए कि किसी समपंचभुज के कोई से चार शीर्ष एक वृत्त पर स्थित होते हैं।
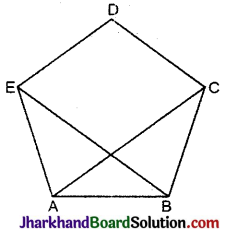
हल :
दिया है समपंचभुज ABCDE
∴ AB = BC = CD = DE = AE.
सिद्ध करना है: कोई चार शीर्ष वृत्त पर स्थित हैं।
रचना : AC तथा BE को मिलाया।
उपपत्ति: ΔABE और ΔABC में,
AB = AB (उभयनिष्ठ)
∠BAE = ∠ABC (समपंचभुज के अन्त:कोण)
AE = BC (दिया है)
ΔABE ≅ ΔABC (SAS नियम से)
अत: ∠AEB = ∠ACB
परन्तु ये कोण भुजा AB द्वारा भुजा के एक ही ओर बनाये गये हैं।
अतः बिन्दु A, B, C और E एक वृत्त पर स्थित हैं। इति सिद्धम् ।
प्रश्न 20.
दिये गये चित्र में ‘O’ वृत्त का केन्द्र है। यदि ∠APB = 40° है, तो ∠AQB का मान ज्ञात करो ।
हल :
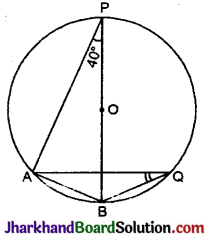
जीवा AB द्वारा ∠APB तथा ∠AQB एक ही वृत्तखण्ड में अन्तरित हैं।
अतः ∠APB = ∠AQB
= 40° (एक ही वृत्तखण्ड के कोण)
∴ ∠AQB =40°.
प्रश्न 21.
दिये गये चित्र में, ∠BOC = 75° तो ∠ACO का मान ज्ञात करो ।
हल :
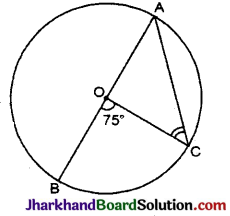
∵ AOB वृत्त का व्यास है।
∴ ∠AOB = 180°
तथा ∠AOC + ∠BOC = 180° (रैखिक कोण युग्म)
⇒ ∠AOC + 75° = 180°
⇒ ∠AOC = 180°- 75° = 105°
अब ΔAOC में
AO = CO (एक ही वृत्त ही त्रिज्याएँ)
∴ ∠OAC = ∠OCA (समान भुजाओं के सम्मुख कोण)
∠AOC + ∠OAC + ∠OCA = 180°
(त्रिभुज के अन्तः कोणों का योग )
105° + ∠OCA + ∠OCA = 180°
2∠OCA = 180° – 105° = 75°
∠OCA = \(\frac {75}{2}\)
∠OCA = 37.5°
प्रश्न 22.
दिये गये चित्र में ABCD एक चक्रीय चतुर्भुज है। यदि ∠PCB = 70° तो ∠BOD का मान बताइए।
हल :
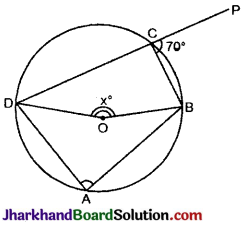
हम जानते हैं कि वृत्त के अन्तर्गत बने चक्रीय चतुर्भुज के बहिष्कोण का मान उस चतुर्भुज के सम्मुख कोण के बराबर होता है।
अतः ∠BAD = 70°
∠BOD = 2∠BAD (वृत्त केन्द्र पर अन्तरित कोण)
अतः ∠BOD = 70° × 2
∴ ∠BOD = 140°
प्रश्न 23.
दिये गये चित्र में वृत्त की जीवाएँ AB = CD तथा ∠OBA = 40° तो ∠COD का मान बताइए।
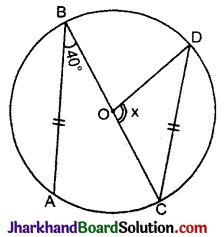
हल :
दिया है AB = CD
तथा OB = OD
∴ ∠OBA = ∠ODC = 40°
ΔOCD एक समद्विबाहु त्रिभुज है।
∴ ∠OCD = ∠ODC = 40°
ΔOCD में
∠ODC + ∠OCD + ∠COD = 180°
⇒ 40° + 40° + ∠COD = 180°
∴ ∠COD (x) = 180° – 40° – 40° = 180° – 80
∴ ∠COD = 100°
![]()
प्रश्न 24.
एक वृत्त की दो जीवाएँ AB तथा CD जिनकी लम्बाइयाँ क्रमशः 6 सेमी तथा 12 सेमी है, एक-दूसरे के समान्तर तथा वृत्त के केन्द्र के एक ही ओर स्थित हैं। यदि दोनों जीवाओं के बीच की दूरी 3 सेमी है तो वृत्त की त्रिज्या ज्ञात करो ।
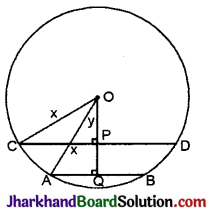
हल :
दिया है AB = 6 सेमी
AQ = \(\frac {1}{2}\)AB = \(\frac {1}{2}\) × 6
AQ = 3 सेमी
CD = 12 सेमी
CP = \(\frac {1}{2}\)CD
= \(\frac {1}{2}\) × 12
CP = 6 सेमी
PQ = 3 सेमी
माना वृत्त की त्रिज्या = x सेमी है।
तथा OP = y सेमी है।
समकोण त्रिभुज CPO में,
अतः CO² = CP² + OP²
⇒ x² = (6)² + y²
⇒ x² = 36 + y² …………….(i)
अब, समकोण त्रिभुज, QOA में,
AQ² = OQ² + AQ²
⇒ x² = (3 + y)² + (3)
⇒ x² = (3 + y)² + 9 …………….(ii)
समी. (i) तथा (ii) की तुलना करने पर,
36 + y² = (3 + y)² + 9
या 36 + y² = 9 + y² + 6y + 9
या 36 – 9 – 9 = 6y
या 18 = 6y
∴ y = \(\frac {18}{6}\) = 3 सेमी
y का मान समीकरण (i) में रखने पर,
∴ x² = 36 + y²
⇒ x² = 36 + (3)²
⇒ x² = 36 + 9 = 45
⇒ x = \(\sqrt{45}\) = \(\sqrt{9 \times 5}\)
∴ x = 3\(\sqrt{5}\)
अतः वृत्त की त्रिज्या = 3\(\sqrt{5}\) सेमी